Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T17:27:05.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-scale structures in high-Reynolds-number rotating Waleffe flow

Published online by Cambridge University Press:  10 December 2019

Shafqat Farooq ,
Martin Huarte-Espinosa  and
Rodolfo Ostilla-Mónico Open the ORCID record for Rodolfo Ostilla-Mónico [Opens in a new window]
Shafqat Farooq
Affiliation:
Cullen College of Engineering, University of Houston, Houston, TX77204, USA
Martin Huarte-Espinosa
Affiliation:
University of Houston’s Hewlett Packard Enterprise Data Science Institute, University of Houston, Houston, TX77204, USA
Rodolfo Ostilla-Mónico*
Affiliation:
Cullen College of Engineering, University of Houston, Houston, TX77204, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

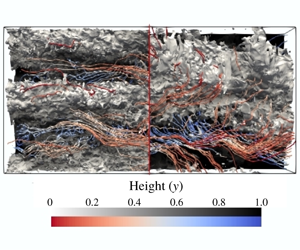
We perform direct numerical simulations of rotating turbulent Waleffe flow, the flow between two parallel plates with a sinusoidal streamwise shear driving force, to study the formation of large-scale structures and the mechanisms for momentum transport. We simulate different cyclonic and anticyclonic rotations in the range of dimensionless rotation numbers (inverse Rossby numbers) $R_{\unicode[STIX]{x1D6FA}}\in [-0.16,2.21]$, and fix the Reynolds number to $Re=3.16\times 10^{3}$, large enough such that the shear transport is almost entirely due to Reynolds stresses and viscous transport is negligible. We find an optimum rotation in the anticyclonic regime at $R_{\unicode[STIX]{x1D6FA}}=0.63$, where a given streamwise momentum transport in the wall-normal direction is achieved with minimum mean energy of the streamwise flow. We link this optimal transport to the strength of large-scale structures, as was done in plane Couette flow by Brauckmann & Eckhardt (J. Fluid Mech., vol. 815, 2017, pp. 149–168). Furthermore, we explore the large-scale structures and their behaviour under spanwise rotation, and find disorganized large structures at $R_{\unicode[STIX]{x1D6FA}}=0$ but highly organized structures in the anticyclonic regime, similar to the rolls in rotating plane Couette and turbulent Taylor–Couette flow. We compare the large-scale structures of plane Couette flow and Waleffe flow, and observe that the streamwise vorticity is localized inside the cores of the rolls. We show that the rolls take energy from the mean flow at long time scales, and relate these structures to eigenvalues of the streamfunction.

JFM classification

Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A26
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Beaume, C., Chini, G. P., Julien, K. & Knobloch, E. 2015 Reduced description of exact coherent states in parallel shear flows. Phys. Rev. E 91 (4), 043010.Google ScholarPubMed
Brauckmann, H. J. & Eckhardt, B. 2013 Intermittent boundary layers and torque maxima in Taylor–Couette flow. Phys. Rev. E 87, 033004.Google Scholar
Brauckmann, H. J. & Eckhardt, B. 2017 Marginally stable and turbulent boundary layers in low-curvature Taylor–Couette flow. J. Fluid Mech. 815, 149–168.CrossRefGoogle Scholar
Brauckmann, H. J., Salewski, M. & Eckhardt, B. 2016 Momentum transport in Taylor–Couette flow with vanishing curvature. J. Fluid Mech. 790.CrossRefGoogle Scholar
Chantry, M., Tuckerman, L. S. & Barkley, D. 2016 Turbulent–laminar patterns in shear flows without walls. J. Fluid Mech. 791, R8.CrossRefGoogle Scholar
Dessup, T., Tuckerman, L. S., Wesfreid, J. E., Barkley, D. & Willis, A. P. 2018 The self-sustaining process in Taylor–Couette flow. Phys. Rev. Fluids 3 (12), 123902.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.CrossRefGoogle Scholar
Eckhardt, B., Schneider, T. M., Höf, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447.CrossRefGoogle Scholar
Einstein, H. A. & Li, H. 1958 Secondary currents in straight channels. EOS Trans. AGU 39 (6), 1085–1088.CrossRefGoogle Scholar
van Gils, D. P. M., Huisman, S. G., Grossmann, S., Sun, C. & Lohse, D. 2012 Optimal Taylor–Couette turbulence. J. Fluid Mech. 706, 118–149.CrossRefGoogle Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High-Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.CrossRefGoogle Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Huisman, S. G., van der Veen, R. C. A., Sun, C. & Lohse, D. 2014 Multiple states in highly turbulent Taylor–Couette flow. Nature Comm. 5, 3820.CrossRefGoogle ScholarPubMed
Jimenez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid. Mech. 44, 27–45.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. L. 1992 Turbulent flow between concentric rotating cylinders at large Reynolds number. Phys. Rev. Fluids 68 (10), 1515–1518.Google ScholarPubMed
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.CrossRefGoogle Scholar
Moser, R. D. & Moin, P.1984 Direct numerical simulation of curved turbulent channel flow. NASA TM 8597.Google Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.CrossRefGoogle Scholar
Pirozzoli, S., Modesti, D., Orlandi, P. & Grasso, F. 2018 Turbulence and secondary motions in square duct flow. J. Fluid Mech. 840, 631–655.CrossRefGoogle Scholar
van der Poel, E. P., Ostilla-Mónico, R., Donners, J. & Verzicco, R. 2015 A pencil distributed finite difference code for strongly turbulent wall-bounded flows. Comput. Fluids 116, 10–16.CrossRefGoogle Scholar
Ravelet, F., Marié, L., Chiffaudel, A. & Daviaud, F. 2004 Multistability and memory effect in a highly turbulent flow: experimental evidence for a global bifurcation. Phys. Rev. Lett. 93, 164501.CrossRefGoogle Scholar
Sacco, F., Verzicco, R. & Ostilla-Mónico, R. 2019 Dynamics and evolution of turbulent Taylor rolls. J. Fluid Mech. 870, 970–987.CrossRefGoogle Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid. Mech. 43, 353–375.CrossRefGoogle Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.CrossRefGoogle Scholar
Tollmien, W.1936 General instability criterion of laminar velocity distributions. NACA TM 792.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flow in cylindrical coordinates. J. Comput. Phys. 123, 402–413.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.CrossRefGoogle Scholar
Zandbergen, P. J. & Dijkstra, D. 1987 Von Kármán swirling flows. Annu. Rev. Fluid Mech. 19 (1), 465–491.CrossRefGoogle Scholar