Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bordji, Mehdi
Gand, Fabien
Brunet, Vincent
and
Deck, Sebastien
2014.
Comparative study of linear and non-linear RANS models for corner flows.
Deck, Sébastien
Gand, Fabien
Brunet, Vincent
and
Ben Khelil, Saloua
2014.
High-fidelity simulations of unsteady civil aircraft aerodynamics: stakes and perspectives. Application of zonal detached eddy simulation.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 372,
Issue. 2022,
p.
20130325.
Deck, Sébastien
Renard, Nicolas
Laraufie, Romain
and
Sagaut, Pierre
2014.
Zonal detached eddy simulation (ZDES) of a spatially developing flat plate turbulent boundary layer over the Reynolds number range 3 150 ⩽ Reθ ⩽ 14 000.
Physics of Fluids,
Vol. 26,
Issue. 2,
Bannier, Amaury
Garnier, Éric
and
Sagaut, Pierre
2015.
Riblet Flow Model Based on an Extended FIK Identity.
Flow, Turbulence and Combustion,
Vol. 95,
Issue. 2-3,
p.
351.
Renard, Nicolas
and
Deck, Sébastien
2015.
On the scale-dependent turbulent convection velocity in a spatially developing flat plate turbulent boundary layer at Reynolds number .
Journal of Fluid Mechanics,
Vol. 775,
Issue. ,
p.
105.
Renard, Nicolas
and
Deck, Sébastien
2015.
Progress in Hybrid RANS-LES Modelling.
Vol. 130,
Issue. ,
p.
203.
Renard, Nicolas
and
Deck, Sébastien
2015.
Improvements in Zonal Detached Eddy Simulation for Wall Modeled Large Eddy Simulation.
AIAA Journal,
Vol. 53,
Issue. 11,
p.
3499.
Riéra, W.
Marty, J.
Castillon, L.
and
Deck, S.
2016.
Zonal Detached-Eddy Simulation Applied to the Tip-Clearance Flow in an Axial Compressor.
AIAA Journal,
Vol. 54,
Issue. 8,
p.
2377.
de Giovanetti, Matteo
Hwang, Yongyun
and
Choi, Haecheon
2016.
Skin-friction generation by attached eddies in turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 808,
Issue. ,
p.
511.
Renard, Nicolas
Deck, Sébastien
and
Sagaut, Pierre
2016.
Progress in Wall Turbulence 2.
Vol. 23,
Issue. ,
p.
379.
Bannier, Amaury
Garnier, Eric
and
Sagaut, Pierre
2016.
Progress in Wall Turbulence 2.
Vol. 23,
Issue. ,
p.
213.
Bannier, Amaury
Garnier, Eric
and
Sagaut, Pierre
2016.
Friction drag reduction achievable by near-wall turbulence manipulation in spatially developing boundary-layer.
Physics of Fluids,
Vol. 28,
Issue. 3,
Renard, Nicolas
and
Deck, Sébastien
2016.
A theoretical decomposition of mean skin friction generation into physical phenomena across the boundary layer.
Journal of Fluid Mechanics,
Vol. 790,
Issue. ,
p.
339.
Verrière, Jonas
Gand, Fabien
and
Deck, Sébastien
2016.
Zonal Detached-Eddy Simulations of a Dual-Stream Jet.
AIAA Journal,
Vol. 54,
Issue. 10,
p.
3176.
Schatzman, David M.
Wilson, Jacob S.
and
Chandrasekhara, M S.
2016.
Synthetic Jet and Turbulent Boundary Layer Interaction Quantification.
Bordji, Mehdi
Gand, Fabien
Deck, Sébastien
and
Brunet, Vincent
2016.
Investigation of a Nonlinear Reynolds-Averaged Navier–Stokes Closure for Corner Flows.
AIAA Journal,
Vol. 54,
Issue. 2,
p.
386.
Yoon, Min
Ahn, Junsun
Hwang, Jinyul
and
Sung, Hyung Jin
2016.
Contribution of velocity-vorticity correlations to the frictional drag in wall-bounded turbulent flows.
Physics of Fluids,
Vol. 28,
Issue. 8,
Im, Hyung Jae
and
Lee, Jae Hwa
2017.
Comparison of superhydrophobic drag reduction between turbulent pipe and channel flows.
Physics of Fluids,
Vol. 29,
Issue. 9,
Pan, Chong
and
Kwon, Yongseok
2018.
Extremely high wall-shear stress events in a turbulent boundary layer.
Journal of Physics: Conference Series,
Vol. 1001,
Issue. ,
p.
012004.
Deck, Sébastien
Weiss, Pierre-Elie
and
Renard, Nicolas
2018.
A rapid and low noise switch from RANS to WMLES on curvilinear grids with compressible flow solvers.
Journal of Computational Physics,
Vol. 363,
Issue. ,
p.
231.
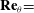 $\mathbf{Re}_{\boldsymbol{\theta}}{=}$13650
$\mathbf{Re}_{\boldsymbol{\theta}}{=}$13650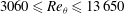 $3060\leq Re_{\theta }\leq 13\, 650$. Some asymptotic trends of global parameters are suggested. Consistently with previous findings, the calculation confirms the occurrence of very large-scale motions approximately
$3060\leq Re_{\theta }\leq 13\, 650$. Some asymptotic trends of global parameters are suggested. Consistently with previous findings, the calculation confirms the occurrence of very large-scale motions approximately 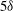 $5\delta $ to
$5\delta $ to 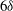 $6 \delta $ long which are meandering with a lateral amplitude of
$6 \delta $ long which are meandering with a lateral amplitude of 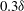 $0.3 \delta $ and which maintain a footprint in the near-wall region. It is shown that these large scales carry a significant amount of Reynolds shear stress and their influence on the skin friction, denoted
$0.3 \delta $ and which maintain a footprint in the near-wall region. It is shown that these large scales carry a significant amount of Reynolds shear stress and their influence on the skin friction, denoted 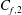 $C_{f,2}$, is revisited through the FIK identity by Fukagata, Iwamoto & Kasagi (Phys. Fluids, vol. 14, 2002, p. L73). It is argued that
$C_{f,2}$, is revisited through the FIK identity by Fukagata, Iwamoto & Kasagi (Phys. Fluids, vol. 14, 2002, p. L73). It is argued that 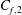 $C_{f,2}$ is the relevant parameter to characterize the high-Reynolds-number turbulent skin friction since the term describing the spatial heterogeneity of the boundary layer also characterizes the total shear stress variations across the boundary layer. The behaviour of the latter term seems to follow some remarkable self-similarity trends towards high Reynolds numbers. A spectral analysis of the weighted Reynolds stress with respect to the distance to the wall and to the wavelength is provided for the first time to our knowledge and allows us to analyse the influence of the largest scales on the skin friction. It is shown that structures with a streamwise wavelength
$C_{f,2}$ is the relevant parameter to characterize the high-Reynolds-number turbulent skin friction since the term describing the spatial heterogeneity of the boundary layer also characterizes the total shear stress variations across the boundary layer. The behaviour of the latter term seems to follow some remarkable self-similarity trends towards high Reynolds numbers. A spectral analysis of the weighted Reynolds stress with respect to the distance to the wall and to the wavelength is provided for the first time to our knowledge and allows us to analyse the influence of the largest scales on the skin friction. It is shown that structures with a streamwise wavelength 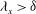 $\lambda _x >\delta $ contribute to more than
$\lambda _x >\delta $ contribute to more than 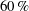 $60\, \%$ of
$60\, \%$ of  $C_{f,2}$, and that those larger than
$C_{f,2}$, and that those larger than 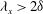 $\lambda _x >2\delta $ still represent approximately
$\lambda _x >2\delta $ still represent approximately 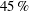 $45\, \%$ of
$45\, \%$ of 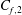 $C_{f,2}$.
$C_{f,2}$.