Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T12:46:47.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Large eddy simulations of turbulent Couette–Poiseuille and Couette flows inside a square duct

Published online by Cambridge University Press:  23 May 2012

Hsin-Wei Hsu ,
Jian-Bin Hsu ,
Wei Lo  and
Chao-An Lin
Hsin-Wei Hsu
Affiliation:
Department of Power Mechanical Engineering, National Tsing Hua University, Hsinchu 300, Taiwan
Jian-Bin Hsu
Affiliation:
Department of Power Mechanical Engineering, National Tsing Hua University, Hsinchu 300, Taiwan
Wei Lo
Affiliation:
Department of Power Mechanical Engineering, National Tsing Hua University, Hsinchu 300, Taiwan
Chao-An Lin*
Affiliation:
Department of Power Mechanical Engineering, National Tsing Hua University, Hsinchu 300, Taiwan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

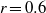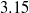Turbulent Couette–Poiseuille and Couette flows at different mean strain rates (velocity ratio of Couette wall to bulk flow, –), in a square duct at a bulk Reynolds number 10 000 are investigated by large eddy simulation. The numerical framework consists of a finite-volume method with a staggered-grid arrangement of dependent variables. Spatial derivatives are approximated using second-order centred differencing, and a fractional-step method is used for temporal integration. Simulations are conducted with 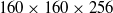grids. Secondary flow near the Couette wall shows a gradual change of vortex size and position as the moving wall velocity increased, where the two clockwise rotating vortices gradually merge in tandem with speed of the moving wall and form a large clockwise vortex. A linear relation is observed to exist between the angle of the two vortices and the parameter , and the angle saturates beyond 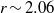. Also, at 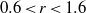, together with a small counter-clockwise corner vortex, this vortex pattern is similar to that observed in the corner region of the duct flow with a free surface. The change of the vortex patterns also influences the dominant transport terms in the streamwise vorticity transport equation. 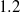Near the moving wall due to the reduction of the streamwise velocity fluctuation at the moving wall, turbulence structure gradually moves towards a rod-like axisymmetric turbulence, and as increases beyond , turbulence reverts to the disc-like structure.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 702 , 10 July 2012 , pp. 89 - 101
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Antonia, R. A., Danh, H. Q. & Prabhu, A. 1977 Response of a turbulent boundary layer to a step change in surface heat flux. J. Fluid Mech. 80, 153–177.CrossRefGoogle Scholar
2. Brogolia, R., Pascarelli, A. & Piomelli, U. 2003 Large eddy simulations of ducts with a free surface. J. Fluid Mech. 484, 223–253.CrossRefGoogle Scholar
3. Gavrilakis, S. 1992 Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 244, 101–129.CrossRefGoogle Scholar
4. Germano, M., Piomelli, U., Moin, P. & Cabot, W. 1991 A dynamic sub grid-scale eddy viscosity model. Phys. Fluids 3, 1760–1765.CrossRefGoogle Scholar
5. Grega, L. M., Wei, T., Leighton, R. I. & Neves, J. C. T. 1995 Turbulenet mixed-boundary flow in a corner formed by a solid wall and a free surface. J. Fluid Mech. 294, 17–46.CrossRefGoogle Scholar
6. Hsu, H. W., Hwang, F. N., Wei, Z. H., Lai, S. H. & Lin, C. A. 2011 A parallel multilevel preconditioned iterative pressure poisson solver for the large-eddy simulation of turbulent flow inside a duct. Comput. Fluids 45, 138–156.CrossRefGoogle Scholar
7. Huser, A. & Biringen, S. 1993 Direct numerical simulation of turbulent flow in a square duct. J. Fluid Mech. 257, 65–95.CrossRefGoogle Scholar
8. Hwang, C. B. & Lin, C. A. 1998 Improved low-Reynolds-number model based on direct numerical simulation data. AIAA J. 36, 38–43.CrossRefGoogle Scholar
9. Hwang, C. B. & Lin, C. A. 2003 Low-Reynolds-number modeling of nonstationary solid boundary flows. AIAA J. 41, 168–175.CrossRefGoogle Scholar
10. Iacovides, H. & Launder, B. E. 1995 Computational fluid dynamics applied to internal gas-turbine blade cooling: a review. Intl J. Heat Fluid Flow 16, 454–470.CrossRefGoogle Scholar
11. Iwamoto, K., Suzuki, Y. & Kasagi, N. 2002 Reynolds number effect on wall turbulence: toward effective feedback control. Intl J. Heat Fluid Flow 23, 678–689.CrossRefGoogle Scholar
12. Kuroda, A., Kasagi, N. & Hirata, M. 1993 Direct numerical simulation of turbulent plane Couette–Poiseuille flows: effect of mean shear rate on the near wall turbulence structures. In Proceedings of Turbulent Shear Flows, p. 241 Springer.Google Scholar
13. Lee, M. J. & Reynolds, W. C. 1985 Numerical experiments on the structure of homogeneous turbulence. In Tech. Rep.. Stanford University, Thermoscience Division.Google Scholar
14. Lilly, D. K. 1992 A proposed modification of the germano subgridscale closure method. Phys. Fluids A 4, 633–635.CrossRefGoogle Scholar
15. Lo, W. & Lin, C. A. 2006 Mean and turbulence structures of Couette–Poiseuille flows at different mean shear rates in a square duct. Phys. Fluids 18, 068103.CrossRefGoogle Scholar
16. Lumley, J. L. 1978 Computational modelling of turbulent flows. Adv. Appl. Mech. 18, 123–176.CrossRefGoogle Scholar
17. Madabhushi, R. K. & Vanka, S. P. 1991 Large eddy simulation of turbulencedriven secondary flow in a square duct. Phys. Fluids A 3, 2734–2745.CrossRefGoogle Scholar
18. Moser, R., Kim, J. & Mansour, N. 1999 Direct numerical simulation of turbulent channel flow up to retau 590. Phys. Fluids 11, 943–945.CrossRefGoogle Scholar
19. Pallares, J. & Davidson, L. 2002 Large Eddy simulations of turbulent heat transfer in stationary and rotating square ducts. Phys. Fluids 14, 2804–2816.CrossRefGoogle Scholar
20. Prandtl, L. 1926 Uber die ausgebildete turbulenz. In Fur Tech. Mech., Zurich (English translation NACA Tech. Memo. 435, 62).Google Scholar
21. Thurlow, E. M. & Klewicki, J. C. 2000 Experimental study of turbulent Poiseuille–Couette flow. Phys. Fluids 4, 865–875.CrossRefGoogle Scholar
22. Uhlmann, M., Pinelli, A., Kawahara, G. & Sekimoto, A. 2007 Marginally turbulent flow in a square duct. J. Fluid Mech. 588, 153–162.CrossRefGoogle Scholar
23. Vazquez, M. Salinas & Metais, O. 2002 Large eddy simulation of the turbulent flow through a heated square duct. J. Fluid Mech. 453, 201–238.CrossRefGoogle Scholar