Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-29T02:03:11.764Z Has data issue: false hasContentIssue false
  • English
  • Français

Large eddy simulations of stratified turbulence: the dynamic Smagorinsky model

Published online by Cambridge University Press:  21 May 2015

Sina Khani  and
Michael L. Waite
Sina Khani*
Affiliation:
Department of Applied Mathematics, University of Waterloo, Waterloo, Ontario, N2L 3G1, Canada
Michael L. Waite
Affiliation:
Department of Applied Mathematics, University of Waterloo, Waterloo, Ontario, N2L 3G1, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

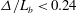The dynamic Smagorinsky model for large eddy simulation (LES) of stratified turbulence is studied in this paper. A maximum grid spacing criterion of ${\it\Delta}/L_{b}<0.24$ is found in order to capture several of the key characteristics of stratified turbulence, where 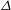${\it\Delta}$ is the filter scale and 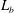$L_{b}$ is the buoyancy scale. These results show that the dynamic Smagorinsky model needs a grid spacing approximately twice as large as the regular Smagorinsky model to reproduce similar results. This improvement on the regular Smagorinsky eddy viscosity approach increases the accuracy of results at small resolved scales while decreasing the computational costs because it allows larger 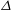${\it\Delta}$. In addition, the eddy dissipation spectra in LES of stratified turbulence present anisotropic features, taking energy out of large horizontal but small vertical scales. This trend is not seen in the non-stratified cases, where the subgrid-scale energy transfer is isotropic. Statistics of the dynamic Smagorinsky coefficient 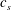$c_{s}$ are investigated; its distribution is peaked around zero, and its standard deviations decrease slightly with increasing stratification. In line with previous findings for unstratified turbulence, regions of increased shear favour smaller 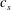$c_{s}$ values; in stratified turbulence, the spatial distribution of the shear, and hence 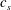$c_{s}$, is dominated by a layerwise pancake structure. These results show that the dynamic Smagorinsky model presents a promising approach for LES when isotropic buoyancy-scale resolving grids are employed.

JFM classification

Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 773 , 25 June 2015 , pp. 327 - 344
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almalkie, S. & de Bruyn Kops, S. M. 2012 Kinetic energy dynamics in forced, homogeneous, and axisymmetric stably stratified turbulence. J. Turbul. 13, 1–32.Google Scholar
Bartello, P. & Tobias, S. M. 2013 Sensitivity of stratified turbulence to the buoyancy Reynolds number. J. Fluid Mech. 725, 1–22.CrossRefGoogle Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
Carati, D., Ghosal, S. & Moin, P. 1995 On the representation of backscatter in dynamic localization models. Phys. Fluids 7 (3), 606–616.CrossRefGoogle Scholar
Deardorff, J. W. 1971 On the magnitude of the subgrid scale eddy coefficient. J. Comput. Phys. 7, 120–133.Google Scholar
Domaradzki, J. A., Liu, W. & Brachet, M. E. 1993 An analysis of subgrid-scale interactions in numerically simulated isotropic turbulence. Phys. Fluids A 5 (7), 1747–1759.Google Scholar
Germano, M. 1992 Turbulence: the filtering approach. J. Fluid Mech. 238, 325–336.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3 (7), 1760–1765.CrossRefGoogle Scholar
Ghosal, S., Lund, T. S., Moin, P. & Akselvoll, K. 1995 A dynamic localization model for large-eddy simulation of turbulent flows. J. Fluid Mech. 286, 229–255.Google Scholar
Hebert, D. A. & de Bruyn Kops, S. M. 2006a Relationship between vertical shear rate and kinetic energy dissipation rate in stably stratified flows. Geophys. Res. Lett. 33, L06602.CrossRefGoogle Scholar
Hebert, D. A. & de Bruyn Kops, S. M. 2006b Predicting turbulence in flows with strong stable stratification. Phys. Fluids 18, 066602.Google Scholar
Herring, J. R. & Métais, O. 1989 Numerical experiments in forced stably stratified turbulence. J. Fluid Mech. 202, 97–115.CrossRefGoogle Scholar
Jiménez, J. R. & Moser, R. D. 2000 Large-eddy simulations: where are we and what can we expect? AIAA J. 38 (4), 605–612.CrossRefGoogle Scholar
Kang, H. S., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 480, 129–160.Google Scholar
Khani, S. & Waite, M. L. 2013 Effective eddy viscosity in stratified turbulence. J. Turbul. 14 (7), 49–70.Google Scholar
Khani, S. & Waite, M. L. 2014 Buoyancy scale effects in large-eddy simulations of stratified turbulence. J. Fluid Mech. 754, 75–97.Google Scholar
Kleissl, J., Kumar, V., Meneveau, C. & Parlange, M. B. 2006 Numerical study of dynamic Smagorinsky model in large-eddy simulation of the atmospheric boundary layer: validation in stable and unstable conditions. Water Resour. Res. 42, W06D10.CrossRefGoogle Scholar
Kraichnan, R. H. 1976 Eddy viscosity in two and three dimensions. J. Atmos. Sci. 33, 1521–1536.Google Scholar
Laval, J.-P., McWilliams, J. C. & Dubrulle, B. 2003 Forced stratified turbulence: successive transition with Reynolds number. Phys. Rev. E 68, 036308.Google Scholar
Lesieur, M. & Métais, O. 1996 New trends in large-eddy simulations of turbulence. Annu. Rev. Fluid Mech. 28, 45–82.CrossRefGoogle Scholar
Lilly, D. K.1967 The representation of small-scale turbulence in numerical simulation experiments. In NCAR Manuscript 281, National Center for Atmospheric Research, Boulder, CO, USA, pp. 99–164.Google Scholar
Lilly, D. K. 1992 A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 4 (3), 633–635.CrossRefGoogle Scholar
Lindborg, E. 2006 The energy cascade in strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Lu, H. & Porté-Agel, F. 2014 On the development of a dynamic nonlinear closure for large-eddy simulation of the atmospheric boundary layer. Boundary-Layer Meteorol. 151 (3), 429–451.Google Scholar
Meneveau, C. 2012 Germano identity-based subgrid-scale modeling: a brief survey of variations on a fertile theme. Phys. Fluids 24, 121301.CrossRefGoogle Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32, 1–32.CrossRefGoogle Scholar
Meneveau, C., Lund, T. S. & Cabot, W. H. R. 1996 A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 319, 353–385.CrossRefGoogle Scholar
Orszag, S. A. 1971 On the elimination of aliasing in finite-difference schemes by filtering high-wavenumber components. J. Atmos. Sci. 28, 1074–1074.2.0.CO;2>CrossRefGoogle Scholar
Paoli, R., Thouron, O., Escobar, J., Picot, J. & Cariolle, D. 2013 High-resolution large-eddy simulations of sub-kilometer-scale turbulence in the upper troposphere lower stratosphere. Atmos. Chem. Phys. Discuss. 13, 31891–31932.Google Scholar
Piomelli, U. 1999 Large-eddy simulation: achievements and challenges. Prog. Aerosp. Sci. 35, 335–362.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Pope, S. B. 2004 Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 6 (35), 1–24.CrossRefGoogle Scholar
Porté-Agel, F., Meneveau, C. & Parlange, M. B. 2000 A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. J. Fluid Mech. 415, 261–284.Google Scholar
Remmler, S. & Hickel, S. 2012 Direct and large eddy simulation of stratified turbulence. Intl J. Heat Fluid Flow 35, 13–24.CrossRefGoogle Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15, 2047–2059.CrossRefGoogle Scholar
Siegel, D. A. & Domaradzki, J. A. 1994 Large-eddy simulation of decaying stably stratified turbulence. J. Phys. Oceanogr. 24, 2353–2386.2.0.CO;2>CrossRefGoogle Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. Part I. The basic experiment. Mon. Weath. Rev. 91 (3), 99–164.Google Scholar
Smith, C. M. & Porté-Agel, F. 2014 An intercomparison of subgrid models for large-eddy simulation of katabatic flows. Q. J. R. Meteorol. Soc. 140 (681), 1294–1303.CrossRefGoogle Scholar
Waite, M. L. 2011 Stratified turbulence at the buoyancy scale. Phys. Fluids A 23, 066602.Google Scholar
Waite, M. L. 2014 Direct numerical simulations of laboratory-scale stratified turbulence. In Modeling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments and Numerical Simulations (ed. von Larcher, T. & Williams, P.), American Geophysical Union, pp. 159–175. Wiley & Sons.Google Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–303.CrossRefGoogle Scholar
Wan, F. & Porté-Agel, F. 2011 Large-eddy simulation of stably-stratified flow over a steep hill. Boundary-Layer Meteorol. 138, 367–384.Google Scholar