Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T10:44:10.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Kármán–Howarth solutions of homogeneous isotropic turbulence

Published online by Cambridge University Press:  07 December 2021

L. Djenidi Open the ORCID record for L. Djenidi [Opens in a new window]  and
R.A. Antonia
L. Djenidi*
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308NSW, Australia
R.A. Antonia
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308NSW, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

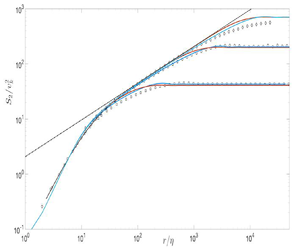
The Kármán–Howarth equation (KHEq) is solved using a closure model to obtain solutions of the second-order moment of the velocity increment, $S_2$, in homogeneous isotropic turbulence (HIT). The results are in good agreement with experimental data for decaying turbulence and are also consistent with calculations based on the three-dimensional energy spectrum for decaying HIT. They differ, however, from those for forced HIT, the difference occurring mainly at large scales. This difference is attributed to the fact that the forcing generates large-scale motions which are not compatible with the KHEq. As the Reynolds number increases, the impact of forcing on the small scales decreases, thus allowing the KHEq and spectrally based solutions to agree well in the range of scales unaffected by forcing. Finally, the results show that the two-thirds law is compatible with the KHEq solutions as the Reynolds number increases to very large, if not infinite, values.

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 932 , 10 February 2022 , A30
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baev, M.K. & Chernykh, G.G. 2010 On Corrsin equation closure. J. Engng Thermophys. 19 (3), 154–169.CrossRefGoogle Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R.A. 1999 A generalization of Yaglom's equation which accounts for the large-scale forcing in heated decaying turbulence. J. Fluid Mech. 391, 359–372.CrossRefGoogle Scholar
Djenidi, L & Antonia, R.A. 2020 Assessment of large-scale forcing in isotropic turbulence using a closed Kármán–Howarth equation. Phys. Fluids 32 (5), 055104.CrossRefGoogle Scholar
Djenidi, L. & Antonia, R.A. 2021 Modelling the third-order velocity structure function in the scaling range at finite Reynolds numbers. J. Math. Phys. 62 (8), 083102.CrossRefGoogle Scholar
Djenidi, L., Antonia, R.A., Lefeuvre, N. & Lemay, J. 2016 Complete self-preservation on the axis of a turbulent round jet. J Fluid Mech. 790, 57–70.CrossRefGoogle Scholar
Djenidi, L., Kamruzzaman, M.. & Antonia, R.A. 2015 Power-law exponent in the transition period of decay in grid turbulence. J. Fluid Mech. 779, 544–555.CrossRefGoogle Scholar
Domaradzki, J.A. & Mellor, G.L. 1984 A simple turbulence closure hypothesis for the triple-velocity correlation functions in homogeneous isotropic turbulence. J. Fluid Mech. 140, 45–61.CrossRefGoogle Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14 (3), 1065–1081.CrossRefGoogle Scholar
Hill, R.J. 2001 Equations relating structure functions of all orders. J. Fluid Mech. 434, 379–388.CrossRefGoogle Scholar
Ishihara, T., Kaneda, Y., Morishita, K., Yokokawa, M. & Uno, A. 2020 Second-order velocity structure functions in direct numerical simulations of turbulence with $R_\lambda$ up to 2250. Phys. Rev. Fluids 5 (10), 104608.CrossRefGoogle Scholar
Ishihara, T., Morishita, K., Yokokawa, M., Uno, A. & Kaneda, Y. 2016 Energy spectrum in high-resolution direct numerical simulations of turbulence. Phys. Rev. Fluids 1 (8), 082403.CrossRefGoogle Scholar
Iyer, K.P., Sreenivasan, K.R. & Yeung, P.K. 2020 Scaling exponents saturate in three-dimensional isotropic turbulence. Phys. Rev. Fluids 5 (5), 054605.CrossRefGoogle Scholar
Kaminsky, J., Birnir, B., Bewley, G.P. & Sinhuber, M. 2020 Reynolds number dependence of the structure functions in homogeneous turbulence. J. Nonlinear Sci. 30 (3), 1081–1114.CrossRefGoogle Scholar
Kolmogorov, A.N. 1941 a The local structure of turbulence in incompressible viscous fluid for very large Reynolds number. Dokl. Akad. Nauk SSSR 30, 299–303. (see also Proc. R. Soc. Lond. A (1991) 434, 9–13).Google Scholar
Kolmogorov, A.N. 1941 b Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 16–18. (see also Proc. R. Soc. Lond. A (1991), 434, 15–17).Google Scholar
Kolmogorov, A.N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.CrossRefGoogle Scholar
Lamorgese, A.G., Caughey, D.A. & Pope, S.B. 2005 Direct numerical simulation of homogeneous turbulence with hyperviscosity. Phys. Fluids 17 (1), 015106.CrossRefGoogle Scholar
Landau, L.D. & Lifshitz, E.M. 1987 Fluid Mechanics: Vol 6 of Course of Theoretical Physics, 2nd English edn revised. Pergamon.Google Scholar
Lundgren, T.S. 2003 Linearly forced isotropic turbulence. In Annual Review Briefs, Center for Turbulence Research ADP014826, University of Minnesota.Google Scholar
McComb, W.D., Yoffe, S.R., Linkmann, M.F. & Berera, A. 2014 Spectral analysis of structure functions and their scaling exponents in forced isotropic turbulence. Phys. Rev. E 90 (5), 053010.CrossRefGoogle ScholarPubMed
Meldi, M., Djenidi, L. & Antonia, R.A. 2021 Sensitivity analysis of the second and third-order velocity structure functions to the Reynolds number in decaying and forced isotropic turbulence using the EDQNM model. Eur. J. Mech. (B/Fluids) 88, 229–242.CrossRefGoogle Scholar
Oberlack, M. & Peters, N. 1993 Closure of the two-point correlation equation as a basis for Reynolds stress models. Appl. Sci. Res. 51 (1–2), 533–538.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Saffman, P.G. 1968 Lectures on homogeneous turbulence. Top. Nonlinear Phys. 485–614.CrossRefGoogle Scholar
Thiesset, F., Antonia, R.A., Danaila, L. & Djenidi, L. 2013 Kármán–Howarth closure equation on the basis of a universal eddy viscosity. Phys. Rev. E 88 (1), 011003.CrossRefGoogle ScholarPubMed
Von Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164, 192–215.CrossRefGoogle Scholar
Yeung, P.K., Zhai, X.M. & Sreenivasan, K.R. 2015 Extreme events in computational turbulence. Proc. Natl Acad. Sci. USA 112 (41), 12633–12638.CrossRefGoogle ScholarPubMed