Article contents
Investigation of tone generation in ideally expanded supersonic planar impinging jets using large-eddy simulation
Published online by Cambridge University Press: 26 October 2016
Abstract
The generation of tones in a supersonic planar jet impinging on a flat plate normally has been investigated by performing compressible large-eddy simulations using low-dissipation and low-dispersion finite differences. At the exit of a straight nozzle of height 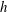 $h$, the jet is ideally expanded, and has a Mach number of 1.28 and a Reynolds number of
$h$, the jet is ideally expanded, and has a Mach number of 1.28 and a Reynolds number of 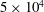 $5\times 10^{4}$. Four distances between the nozzle and the plate between
$5\times 10^{4}$. Four distances between the nozzle and the plate between 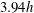 $3.94h$ and
$3.94h$ and 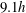 $9.1h$ have been considered. Flow snapshots and mean velocity fields are first presented. The variations of turbulence intensities and of the convection velocity in the jet shear layers are then examined. The properties of the jet near fields are subsequently described, in particular by applying Fourier decomposition to the pressure fields. Several coexisting tones appear to be generated by aeroacoustic feedback loops establishing between the nozzle lip and the flat plate, which also lead to the presence of hydrodynamic–acoustic standing waves. The tone frequencies are consistent with those given by the aeroacoustic feedback model and with measurements for high-aspect-ratio rectangular jets. The jet oscillation modes at these frequencies are characterized, and found to agree with experimental data. Their symmetric or antisymmetric natures are shown to be well predicted by a wave analysis carried out using a vortex sheet model of the jet, providing the allowable frequency ranges for the upstream-propagating acoustic waves. Thus, it is possible, for an ideally expanded impinging planar jet to predict both the frequencies of the tones and the symmetric or antisymmetric nature of the corresponding oscillation modes by combining the aeroacoustic feedback model and the wave analysis.
$9.1h$ have been considered. Flow snapshots and mean velocity fields are first presented. The variations of turbulence intensities and of the convection velocity in the jet shear layers are then examined. The properties of the jet near fields are subsequently described, in particular by applying Fourier decomposition to the pressure fields. Several coexisting tones appear to be generated by aeroacoustic feedback loops establishing between the nozzle lip and the flat plate, which also lead to the presence of hydrodynamic–acoustic standing waves. The tone frequencies are consistent with those given by the aeroacoustic feedback model and with measurements for high-aspect-ratio rectangular jets. The jet oscillation modes at these frequencies are characterized, and found to agree with experimental data. Their symmetric or antisymmetric natures are shown to be well predicted by a wave analysis carried out using a vortex sheet model of the jet, providing the allowable frequency ranges for the upstream-propagating acoustic waves. Thus, it is possible, for an ideally expanded impinging planar jet to predict both the frequencies of the tones and the symmetric or antisymmetric nature of the corresponding oscillation modes by combining the aeroacoustic feedback model and the wave analysis.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
Gojon et al. Movie 1
Animation in the (x,y) plane of the density in the jet and close to the flat plate and of the pressure fluctuations for (a) JetL3.9, (b) JetL5.5, (c) JetL8.3 and (d) JetL9.1. The colour scale ranges from 1 to 2 kg.m-3 for density, from blue to red and from -7500 to 7500 Pa for pressure, from black to white. The nozzle is in black.
- 73
- Cited by



