Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T16:05:41.581Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant states in inclined layer convection. Part 2. Bifurcations and connections between branches of invariant states

Published online by Cambridge University Press:  09 July 2020

Florian Reetz ,
Priya Subramanian  and
Tobias M. Schneider Open the ORCID record for Tobias M. Schneider [Opens in a new window]
Florian Reetz
Affiliation:
Emergent Complexity in Physical Systems Laboratory (ECPS), Ecole Polytechnique Fédérale de Lausanne, CH-1015, Switzerland
Priya Subramanian
Affiliation:
School of Mathematics, University of Leeds, LeedsLS2 9JT, UK Mathematical Institute, University of Oxford, Woodstock Road, OxfordOX2 6GG, UK
Tobias M. Schneider*
Affiliation:
Emergent Complexity in Physical Systems Laboratory (ECPS), Ecole Polytechnique Fédérale de Lausanne, CH-1015, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

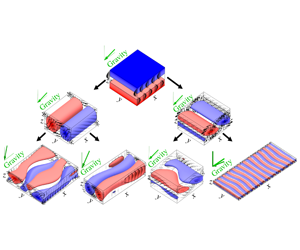
Convection in a layer inclined against gravity is a thermally driven non-equilibrium system, in which both buoyancy and shear forces drive spatio-temporally complex flows. As a function of the strength of thermal driving and the angle of inclination, a multitude of convection patterns is observed in experiments and numerical simulations. Several observed patterns have been linked to exact invariant states of the fully nonlinear three-dimensional Oberbeck–Boussinesq equations. These exact equilibria, travelling waves and periodic orbits reside in state space and, depending on their stability properties, are transiently visited by the dynamics or act as attractors. To explain the dependence of observed convection patterns on control parameters, we study the parameter dependence of the state space structure. Specifically, we identify the bifurcations that modify the existence, stability and connectivity of invariant states. We numerically continue exact invariant states underlying spatially periodic convection patterns at $Pr=1.07$ under changing control parameters for a temperature difference between the walls and inclination angle. The resulting state branches cover various inclinations from horizontal layer convection to vertical layer convection and beyond. The collection of all computed branches represents an extensive bifurcation network connecting 16 different invariant states across control parameter values. Individual bifurcation structures are discussed in detail and related to the observed complex dynamics of individual convection patterns. Together, the bifurcations and associated state branches indicate at what control parameter values which invariant states coexist. This provides a nonlinear framework to explain the multitude of complex flow dynamics arising in inclined layer convection.

JFM classification

Nonlinear Dynamical Systems: Pattern formation Nonlinear Dynamical Systems: Bifurcation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 898 , 10 September 2020 , A23
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Argyris, J., Faust, G. & Haase, M. 1993 Routes to chaos and turbulence. A computational introduction. Phil. Trans. R. Soc. Lond. A 344 (1671), 207–234.Google Scholar
Bergeon, A. & Knobloch, E. 2002 Natural doubly diffusive convection in three-dimensional enclosures. Phys. Fluids 14 (9), 3233–3250.CrossRefGoogle Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32 (1), 709–778.CrossRefGoogle Scholar
Busse, F. H. 1978 Non-linear properties of thermal convection. Rep. Prog. Phys. 41 (12), 1929–1967.CrossRefGoogle Scholar
Busse, F. H. & Clever, R. M. 1979 Instabilities of convection rolls in a fluid of moderate Prandtl number. J. Fluid Mech. 91 (2), 319–335.CrossRefGoogle Scholar
Busse, F. H. & Clever, R. M. 1992 Three-dimensional convection in an inclined layer heated from below. J. Engng Maths 26 (1), 1–19.CrossRefGoogle Scholar
Busse, F. H. & Clever, R. M. 1996 The sequence-of-bifurcations approach towards an understanding of complex flows. In Mathematical Modeling and Simulation in Hydrodynamic Stability (ed. Riahi, D. N.), pp. 15–34. World Scientific.CrossRefGoogle Scholar
Busse, F. H. & Clever, R. M. 2000 Bursts in inclined layer convection. Phys. Fluids 12 (8), 2137–2140.CrossRefGoogle Scholar
Busse, F. H. & Whitehead, J. A. 1974 Oscillatory and collective instabilities in large Prandtl number convection. J. Fluid Mech. 66 (1), 67–79.CrossRefGoogle Scholar
Chen, Y.-M. & Pearlstein, A. J. 1989 Stability of free-convection flows of variable-viscosity fluids in vertical and inclined slots. J. Fluid Mech. 198, 513–541.CrossRefGoogle Scholar
Chossat, P. & Iooss, G.The Couette–Taylor Problem, Applied Mathematical Sciences, vol. 102. Springer.Google Scholar
Clever, R. M. 1973 Finite amplitude longitudal convection rolls in an inclined layer. Trans. ASME J. Heat Transfer 95 (3), 407–408.CrossRefGoogle Scholar
Clever, R. M. & Busse, F. H. 1977 Instabilities of longitudinal convection rolls in an inclined layer. J. Fluid Mech. 81 (1), 107–127.CrossRefGoogle Scholar
Clever, R. M. & Busse, F. H. 1992 Three-dimensional convection in a horizontal fluid layer subjected to a constant shear. J. Fluid Mech. 234, 511–527.CrossRefGoogle Scholar
Clever, R. & Busse, F. 1995 Tertiary and quarternary solutions for convection in a vertical fluid layer heated from the side. Chaos, Solitons Fractals 5 (10), 1795–1803.CrossRefGoogle Scholar
Cross, M. & Greenside, H. 2009 Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge University Press.CrossRefGoogle Scholar
Daniels, K. E. & Bodenschatz, E. 2002 Defect turbulence in inclined layer convection. Phys. Rev. Lett. 88 (3), 034501.CrossRefGoogle ScholarPubMed
Daniels, K. E., Brausch, O., Pesch, W. & Bodenschatz, E. 2008 Competition and bistability of ordered undulations and undulation chaos in inclined layer convection. J. Fluid Mech. 597, 261–282.CrossRefGoogle Scholar
Daniels, K., Plapp, B. & Bodenschatz, E. 2000 Pattern formation in inclined layer convection. Phys. Rev. Lett. 84 (23), 5320–5323.CrossRefGoogle ScholarPubMed
Daniels, K. E., Wiener, R. J. & Bodenschatz, E. 2003 Localized transverse bursts in inclined layer convection. Phys. Rev. Lett. 91 (11), 114501.CrossRefGoogle ScholarPubMed
Dijkstra, H. A., Wubs, F. W., Cliffe, A. K., Doedel, E., Hazel, A. L., Lucarini, V., Salinger, A. G., Phipps, E. T., Sanchez-Umbria, J., Schuttelaars, H. et al. 2014 Numerical bifurcation methods and their application to fluid dynamics: analysis beyond simulation. Commun. Comput. Phys. 15 (1), 1–45.CrossRefGoogle Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39 (1), 447–468.CrossRefGoogle Scholar
Fujimura, K. & Kelly, R. E. 1993 Mixed mode convection in an inclined slot. J. Fluid Mech. 246, 545–568.CrossRefGoogle Scholar
Gershuni, G. Z. & Zhukhovitskii, E. M. 1969 Stability of plane-parallel convective motion with respect to spatial perturbations. Prikl. Mat. Mekh. 33 (5), 855–860.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.CrossRefGoogle Scholar
Gibson, J. F., Reetz, F., Azimi, S., Ferraro, A., Kreilos, T., Schrobsdorff, H., Farano, M., Yesil, A. F., Schütz, S. S., Culpo, M. et al. 2019 Channelflow 2.0., (in preparation). Available at: https://www.channelflow.ch.Google Scholar
Golubitsky, M. & Stewart, I. 2002 The Symmetry Perspective. Birkhäuser Basel.CrossRefGoogle Scholar
Guckenheimer, J. & Holmes, P. 1983 Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields, Applied Mathematical Sciences, vol. 42. Springer.CrossRefGoogle Scholar
Hart, J. E. 1971 Transition to a wavy vortex régime in convective flow between inclined plates. J. Fluid Mech. 48 (2), 265–271.CrossRefGoogle Scholar
Juniper, M. P. & Sujith, R. 2018 Sensitivity and nonlinearity of thermoacoustic oscillations. Annu. Rev. Fluid Mech. 50 (1), 661–689.CrossRefGoogle Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44 (1), 203–225.CrossRefGoogle Scholar
Kerswell, R. R. 2005 Recent progress in understanding the transition to turbulence in a pipe. Nonlinearity 18 (6), R17–R44.CrossRefGoogle Scholar
Knobloch, E. 1986 Oscillatory convection in binary mixtures. Phys. Rev. A 34 (2), 1538–1549.CrossRefGoogle ScholarPubMed
Knobloch, E. 2015 Spatial localization in dissipative systems. Annu. Rev. Condens. Matter Phys. 6 (1), 325–359.CrossRefGoogle Scholar
Krupa, M. 1997 Robust heteroclinic cycles. J. Nonlinear Sci. 7 (2), 129–176.CrossRefGoogle Scholar
Krupa, M. & Melbourne, I. 1995 Asymptotic stability of heteroclinic cycles in systems with symmetry. Ergod. Theory Dyn. Sys. 15 (1), 121–147.CrossRefGoogle Scholar
Lenton, T. M., Held, H., Kriegler, E., Hall, J. W., Lucht, W., Rahmstorf, S. & Joachim, H. 2008 Tipping elements in the Earth’s climate system. Proc. Natl Acad. Sci. USA 105 (6), 1786–1793.CrossRefGoogle ScholarPubMed
Lorenz, E. N. 1963 Deterministic nonperiodic flow. J. Atmos. Sci. 20 (2), 130–141.2.0.CO;2>CrossRefGoogle Scholar
Mizushima, J. & Tanaka, H. 2002a Transition routes of natural convection in a vertical fluid layer. J. Phys. Soc. Japan 71 (12), 2898–2906.CrossRefGoogle Scholar
Mizushima, J. & Tanaka, H. 2002b Transitions of natural convection in a vertical fluid layer. Phys. Fluids 14 (4), L21–L24.CrossRefGoogle Scholar
Pinter, A., Lücke, M. & Hoffmann, C. 2006 Competition between traveling fluid waves of left and right spiral vortices and their different amplitude combinations. Phys. Rev. Lett. 96 (4), 1–4.CrossRefGoogle ScholarPubMed
Pomeau, Y. & Manneville, P. 1980 Intermittent transition to turbulence in dissipative dynamical systems. Commun. Math. Phys. 74, 189–197.CrossRefGoogle Scholar
Reetz, F. & Schneider, T. M. 2020 Invariant states in inclined layer convection. Part 1. Temporal transitions along dynamical connections between invariant states. J. Fluid Mech.Google Scholar
Ruth, B. D. W., Hollands, K. G. T. & Raithby, A. N. D. G. D. 1980 On free convection experiments in inclined air layers heated from below. J. Fluid Mech. 96 (3), 461–479.CrossRefGoogle Scholar
Sanchez, J., Net, M., Garcıia-Archilla, B. & Simo, C. 2004 Newton–Krylov continuation of periodic orbits for Navier–Stokes flows. J. Comput. Phys. 201 (1), 13–33.CrossRefGoogle Scholar
Schaeffer, D. G. & Cain, J. W. 2016 Ordinary Differential Equations: Basics and Beyond, Texts in Applied Mathematics, vol. 65. Springer.CrossRefGoogle Scholar
Subramanian, P., Brausch, O., Daniels, K. E., Bodenschatz, E., Schneider, T. M. & Pesch, W. 2016 Spatio-temporal patterns in inclined layer convection. J. Fluid Mech. 794, 719–745.CrossRefGoogle Scholar
Subramanian, P., Pesch, W. & Schneider, T. M. 2015 Tertiary patterns in inclined layer convection. In Proceedings of the 15th European Turbulence Conference, 25–28 August, 2015, Delft, The Netherlands. Euromech.Google Scholar
Suri, B., Tithof, J., Grigoriev, R. O. & Schatz, M. F. 2017 Forecasting fluid flows using the geometry of turbulence. Phys. Rev. Lett. 118 (11), 114501.CrossRefGoogle ScholarPubMed
Tagg, R., Edwards, W. S., Swinney, H. L. & Marcus, S. 1989 Nonlinear standing waves in Couette–Taylor flow. Phys. Rev. A 39 (7), 3734–3738.CrossRefGoogle ScholarPubMed
Tuckerman, L. S. & Barkley, D. 1990 Bifurcation analysis of the Eckhaus instability. Physica D: Nonlinear Phenomena 46 (1), 57–86.CrossRefGoogle Scholar
Vest, C. M. & Arpaci, V. S. 1969 Stability of natural convection in a vertical slot. J. Fluid Mech. 36 (1), 1–15.CrossRefGoogle Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.CrossRefGoogle Scholar
Waleffe, F., Boonkasame, A. & Smith, L. M. 2015 Heat transport by coherent Rayleigh–Bénard convection. Phys. Fluids 27 (5), 051702.CrossRefGoogle Scholar
Weiss, S., Seiden, G. & Bodenschatz, E. 2012 Pattern formation in spatially forced thermal convection. New J. Phys. 14 (5), 053010.Google Scholar