Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Masunaga, Eiji
Uchiyama, Yusuke
Suzue, Yota
and
Yamazaki, Hidekatsu
2018.
Dynamics of Internal Tides Over a Shallow Ridge Investigated With a High‐Resolution Downscaling Regional Ocean Model.
Geophysical Research Letters,
Vol. 45,
Issue. 8,
p.
3550.
Vladoiu, Anda
Bouruet-Aubertot, Pascale
Cuypers, Yannis
Ferron, Bruno
Schroeder, Katrin
Borghini, Mireno
Leizour, Stephane
and
Ismail, Sana Ben
2018.
Turbulence in the Sicily Channel from microstructure measurements.
Deep Sea Research Part I: Oceanographic Research Papers,
Vol. 137,
Issue. ,
p.
97.
Shakespeare, Callum J.
and
McC. Hogg, Andrew
2019.
On the Momentum Flux of Internal Tides.
Journal of Physical Oceanography,
Vol. 49,
Issue. 4,
p.
993.
Masunaga, Eiji
Uchiyama, Yusuke
and
Yamazaki, Hidekatsu
2019.
Strong Internal Waves Generated by the Interaction of the Kuroshio and Tides over a Shallow Ridge.
Journal of Physical Oceanography,
Vol. 49,
Issue. 11,
p.
2917.
Kaminski, A.K.
and
Flynn, M.R.
2020.
Modal decomposition of polychromatic internal wave fields in arbitrary stratifications.
Wave Motion,
Vol. 95,
Issue. ,
p.
102549.
Lahaye, Noé
Gula, Jonathan
and
Roullet, Guillaume
2020.
Internal Tide Cycle and Topographic Scattering Over the North Mid‐Atlantic Ridge.
Journal of Geophysical Research: Oceans,
Vol. 125,
Issue. 12,
Howland, Christopher J.
Taylor, John R.
and
Caulfield, C.P.
2021.
Shear-induced breaking of internal gravity waves.
Journal of Fluid Mechanics,
Vol. 921,
Issue. ,
Johnston, T. M. Shaun
and
Ou, Celia Y.
2021.
Momentum Flux Convergence From Internal Tides in the North Equatorial Countercurrent Upstream of a Submarine Ridge Near Merir Island, Palau.
Journal of Geophysical Research: Oceans,
Vol. 126,
Issue. 2,
Stastna, Marek
Coutino, Aaron
and
Walter, Ryan K.
2021.
The effect of strong shear on internal solitary-like waves.
Nonlinear Processes in Geophysics,
Vol. 28,
Issue. 4,
p.
585.
Bai, Xiaolin
Lamb, Kevin G.
and
da Silva, José C. B.
2021.
Small‐Scale Topographic Effects on the Generation of Along‐Shelf Propagating Internal Solitary Waves on the Amazon Shelf.
Journal of Geophysical Research: Oceans,
Vol. 126,
Issue. 8,
Puthan, Pranav
Pawlak, Geno
and
Sarkar, Sutanu
2022.
Wake Vortices and Dissipation in a Tidally Modulated Flow Past a Three‐Dimensional Topography.
Journal of Geophysical Research: Oceans,
Vol. 127,
Issue. 8,
Musgrave, Ruth
Pollmann, Friederike
Kelly, Samuel
and
Nikurashin, Maxim
2022.
Ocean Mixing.
p.
117.
Masunaga, Eiji
2023.
Mixing processes and hydraulic environments in coastal regions: Internal tides and mixing phenomena.
Oceanography in Japan,
Vol. 32,
Issue. 2,
p.
37.
Baumann, Till M.
and
Fer, Ilker
2023.
Trapped tidal currents generate freely propagating internal waves at the Arctic continental slope.
Scientific Reports,
Vol. 13,
Issue. 1,
Bai, Xiaolin
Lamb, Kevin G.
Liu, Zhiyu
and
Hu, Jianyu
2023.
Intermittent Generation of Internal Solitary‐Like Waves on the Northern Shelf of the South China Sea.
Geophysical Research Letters,
Vol. 50,
Issue. 6,
Bendinger, Arne
Cravatte, Sophie
Gourdeau, Lionel
Brodeau, Laurent
Albert, Aurélie
Tchilibou, Michel
Lyard, Florent
and
Vic, Clément
2023.
Regional modeling of internal-tide dynamics around New Caledonia – Part 1: Coherent internal-tide characteristics and sea surface height signature.
Ocean Science,
Vol. 19,
Issue. 4,
p.
1315.
Zhao, Zhongxiang
and
Qiu, Bo
2023.
Seasonal West‐East Seesaw of M2 Internal Tides From the Luzon Strait.
Journal of Geophysical Research: Oceans,
Vol. 128,
Issue. 3,
Klema, Matthew R.
and
Venayagamoorthy, Subhas K.
2024.
Energetics of mode-1 internal waves interacting with topographic ridges of varying height and slope.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
Masunaga, Eiji
Tamura, Hitoshi
and
Uchiyama, Yusuke
2024.
Shoaling Internal Tides Propagating From a Shallow Ridge Modulated by the Kuroshio.
Journal of Geophysical Research: Oceans,
Vol. 129,
Issue. 9,
Tian, Yonghe
Bai, Xiaolin
Wang, Chuanyin
and
Liu, Zhiyu
2025.
Tidal energetics in the eddying South China Sea from a high-resolution numerical simulation.
Progress in Oceanography,
Vol. 231,
Issue. ,
p.
103418.
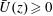 $\bar{U}(z)\geqslant 0$ confined to a surface layer lying well above the ridge. The current introduces asymmetries in the generated wave field. For sufficiently narrow ridges the upstream energy flux is larger than the downstream flux while the opposite is the case for sufficiently wide ridges. The total energy flux radiating away from the ridge is not significantly affected by the current. Mean second-order currents and pressure fields are shown to make important contributions to the total energy flux. A first-order linear theory, valid for a general stratification and surface current, which accurately predicts the wave field is also developed.
$\bar{U}(z)\geqslant 0$ confined to a surface layer lying well above the ridge. The current introduces asymmetries in the generated wave field. For sufficiently narrow ridges the upstream energy flux is larger than the downstream flux while the opposite is the case for sufficiently wide ridges. The total energy flux radiating away from the ridge is not significantly affected by the current. Mean second-order currents and pressure fields are shown to make important contributions to the total energy flux. A first-order linear theory, valid for a general stratification and surface current, which accurately predicts the wave field is also developed.


