Article contents
Intensification of non-uniformity in convergent near-conical hypersonic flow
Published online by Cambridge University Press: 22 November 2021
Abstract
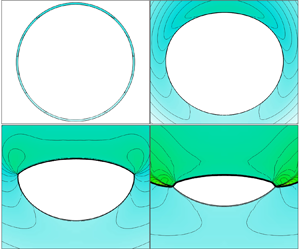
The inevitable formation of a Mach disk at the central axis of a convergent conical shock wave may suffer from fundamental changes when the flow deviates from the axisymmetric condition. In this paper, the behaviours of near-conical shocks, which are generated by a circular ring wedge of  $10^{\circ }$ at typical angles of attack (AoAs), are investigated at a free stream Mach number of 6 in a shock tunnel. To reveal the characteristics and mechanism of the flow, numerical analyses are carried out under the same conditions. The results indicate that when the flow deviates from axial symmetry, the circumferential non-uniformity is remarkably intensified as the shock converges downstream. The converging centre shifts against the inclination of the incoming flow and moves to the leeward side. For a sufficiently small AoA, the formation of a Mach disk remains similar to that in the axisymmetric case, although the Mach disk shrinks in size and is slightly flattened. As the circumferential non-uniformity of the shock increases at an AoA of approximately
$10^{\circ }$ at typical angles of attack (AoAs), are investigated at a free stream Mach number of 6 in a shock tunnel. To reveal the characteristics and mechanism of the flow, numerical analyses are carried out under the same conditions. The results indicate that when the flow deviates from axial symmetry, the circumferential non-uniformity is remarkably intensified as the shock converges downstream. The converging centre shifts against the inclination of the incoming flow and moves to the leeward side. For a sufficiently small AoA, the formation of a Mach disk remains similar to that in the axisymmetric case, although the Mach disk shrinks in size and is slightly flattened. As the circumferential non-uniformity of the shock increases at an AoA of approximately  $3^{\circ }$, a pair of kinks separate the shock surface into two discontinuous segments with the stronger shock segment on the windward side and the weaker shock segment on the leeward side. When the AoA increases further, the shrinkage of the Mach disk continuously occurs, and the Mach disk is eventually replaced by a regular reflection. The discontinuity of a convergent shock with flattening on the separated shock segments and the insufficient strength increase during the subsequent convergence are responsible for the appearance of regular reflection.
$3^{\circ }$, a pair of kinks separate the shock surface into two discontinuous segments with the stronger shock segment on the windward side and the weaker shock segment on the leeward side. When the AoA increases further, the shrinkage of the Mach disk continuously occurs, and the Mach disk is eventually replaced by a regular reflection. The discontinuity of a convergent shock with flattening on the separated shock segments and the insufficient strength increase during the subsequent convergence are responsible for the appearance of regular reflection.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 2
- Cited by



