Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T12:46:02.997Z Has data issue: false hasContentIssue false
  • English
  • Français

Instantaneous energy and enstrophy variations in Euler-alpha point vortices via triple collapse

Published online by Cambridge University Press:  21 May 2012

Takashi Sakajo
Takashi Sakajo*
Affiliation:
Department of Mathematics, Hokkaido University CREST, Japan Science and Technology Agency, Sapporo, Hokkaido, 060-0810, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It has been pointed out that the anomalous enstrophy dissipation in non-smooth weak solutions of the two-dimensional Euler equations has a clue to the emergence of the inertial range in the energy density spectrum of two-dimensional turbulence corresponding to the enstrophy cascade as the viscosity coefficient tends to zero. However, it is uncertain how non-smooth weak solutions can dissipate the enstrophy. In the present paper, we construct a weak solution of the two-dimensional Euler equations from that of the Euler- equations proposed by Holm, Marsden & Ratiu (Phys. Rev. Lett., vol. 80, 1998, pp. 4173–4176) by taking the limit of 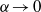. To accomplish this task, we introduce the -point-vortex (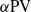) system, whose evolution corresponds to a unique global weak solution of the two-dimensional Euler- equations in the sense of distributions (Oliver & Shkoller, Commun. Part. Diff. Equ., vol. 26, 2001, pp. 295–314). Since the 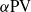system is a formal regularization of the point-vortex system and it is known that, under a certain special condition, three point vortices collapse self-similarly in finite time (Kimura, J. Phys. Soc. Japan, vol. 56, 1987, pp. 2024–2030), we expect that the evolution of three -point vortices for the same condition converges to a singular weak solution of the Euler- equations that is close to the triple collapse as 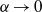, which is examined in the paper. As a result, we find that the three -point vortices collapse to a point and then expand to infinity self-similarly beyond the critical time in the limit. We also show that the Hamiltonian energy and a kinematic energy acquire a finite jump discontinuity at the critical time, but the energy dissipation rate converges to zero in the sense of distributions. On the other hand, an enstrophy variation converges to the 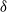measure with a negative mass, which indicates that the enstrophy dissipates in the distributional sense via the self-similar triple collapse. Moreover, even if the special condition is perturbed, we can confirm numerically the convergence to the singular self-similar evolution with the enstrophy dissipation. This indicates that the self-similar triple collapse is a robust mechanism of the anomalous enstrophy dissipation in the sense that it is observed for a certain range of the parameter region.

JFM classification

Mathematical Foundations: Hamiltonian theory Nonlinear Dynamical Systems: Low-dimensional models Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 702 , 10 July 2012 , pp. 188 - 214
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Aref, H. 1979 Motion of three vortices. Phys. Fluids 22 (3), 393–400.CrossRefGoogle Scholar
2. Bardos, C., Linshiz, J. S. & Titi, E. S. 2010 Global regularity and convergence of a Birkhoff–Rott- approximation of the dynamics of vortex sheets of the two-dimensional Euler equations. Commun. Pure Appl. Maths 63, 697–746.CrossRefGoogle Scholar
3. Batchelor, G. K. 1969 Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids Supppl. II 12, 233–239.CrossRefGoogle Scholar
4. Chen, S., Foias, C., Holm, D. D., Olson, E., Titi, E. S. & Wynne, S. 1998 Camasa–Holm equations as a closure model for turbulent channel and pipe flow. Phys. Rev. Lett. 81 (24), 5338–5341.CrossRefGoogle Scholar
5. Chen, S., Holm, D. D., Margolin, L. G. & Zhang, R. 1999 Direct numerical simulations of the Navier–Stokes alpha model. Physica D 133, 66–83.CrossRefGoogle Scholar
6. Constantin, P. 2001 An Eulerian–Lagrangian approach to the Navier–Stokes equations. Commun. Math. Phys. 216, 663–686.CrossRefGoogle Scholar
7. Constantin, P., E, W. & Titi, E. S. 1994 Onsager’s conjecture on the energy conservation for solutions of Euler’s equation. Commun. Math. Phys. 165, 207–209.CrossRefGoogle Scholar
8. Delroit, J.-M. 1991 Existence de nappe de tourbillion en dimension deux. J. Am. Math. Soc. 4, 553–586.CrossRefGoogle Scholar
9. Diperna, R. J. & Majda, A. J. 1987 Concentrations in regularizations for 2-D incompressible flow. Commun. Pure Appl. Maths 40, 301–345.CrossRefGoogle Scholar
10. Duchon, J. & Robert, R. 2000 Inertial energy dissipation for weak solutions of incompressible Euler and Navier–Stokes equations. Nonlinearity 13, 249–255.CrossRefGoogle Scholar
11. Eyink, G. L. 2001 Dissipation in turbulence solutions of 2D Euler equations. Nonlinearity 14, 787–802.CrossRefGoogle Scholar
12. Eyink, G. L. 2003 Local 4/5-law and energy dissipation anomaly in turbulence. Nonlinearity 21, 1233–1252.Google Scholar
13. Eyink, G. L. & Sreenivasan, K. R. 2006 Onsager and the theory of hydrodynamic turbulence. Rev. Mod. Phys. 78, 87–135.CrossRefGoogle Scholar
14. Foias, C., Holm, D. D. & Titi, E. S. 2001 The Navier–Stokes-alpha model of fluid turbulence. Physica D 152–153, 505–519.CrossRefGoogle Scholar
15. Foias, C., Holm, D. D. & Titi, E. S. 2002 The three dimensional viscous Camassa–Holm equations, and their relation to the Navier–Stokes equations and turbulence theory. J. Dyn. Diff. Equ. 14, 1–35.CrossRefGoogle Scholar
16. Holm, D. D. 2002 Variational principles for Lagrangian-averaged fluid dynamics. J. Phys. A 35, 679–688.CrossRefGoogle Scholar
17. Holm, D. D. & Marsden, J. E. 1998 The Euler–Poincaré equations and semidirect products with applications to continuum theories. Adv. Maths 137, 1–81.CrossRefGoogle Scholar
18. Holm, D. D., Marsden, J. E. & Ratiu, T. S. 1998 Euler–Poincaré models of ideal fluids with nonlinear dispersion. Phys. Rev. Lett. 80 (19), 4173–4176.CrossRefGoogle Scholar
19. Holm, D. D., Nitsche, M. & Putkaradze, V. 2006 Euler-alpha and vortex blob regularization of vortex filament and vortex sheet motion. J. Fluid Mech. 555, 149–176.CrossRefGoogle Scholar
20. Hou, T. Y. & Li, C. 2006 On global well-posedness of the Lagrangian averaged Euler equations. SIAM J. Math. Anal. 38 (3), 782–794.CrossRefGoogle Scholar
21. Kimura, Y. 1987 Similarity solution of two-dimensional point vortices. J. Phys. Soc. Japan 56, 2024–2030.CrossRefGoogle Scholar
22. Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.CrossRefGoogle Scholar
23. Leimkuhler, B. & Reich, S. 2005 Simulating Hamiltonian Dynamics. Cambridge University Press.CrossRefGoogle Scholar
24. Leith, C. E. 1968 Diffusion approximation for two-dimensional turbulence. Phys. Fluids 11, 671–672.CrossRefGoogle Scholar
25. Linshiz, J. S. & Titi, E. S. 2010 On the convergence rate of the Euler-, an inviscid second-grade complex fluid, model to the Euler equations. J. Stat. Phys. 138, 305–332.CrossRefGoogle Scholar
26. Lunasin, E., Kurien, S., Taylor, M. A. & Titi, E. S. 2007 A study of the Navier–Stokes- model for two-dimensional turbulence. J. Turbul. 8, 1–21.CrossRefGoogle Scholar
27. Marsden, J. E. & Shkoller, S. 2003 The anisotropic Lagrangian averaged Euler and Navier–Stokes equations. Arch. Rat. Mech. Anal. 166, 27–46.CrossRefGoogle Scholar
28. Mohseni, K., Kosović, B., Shkoller, S. & Marsden, J. E. 2003 Numerical simulations of the Lagrangian averaged Navier–Stokes equations for homogeneous isotropic turbulence. Phys. Fluids 15 (2), 524–544.CrossRefGoogle Scholar
29. Newton, P. K. 2001 The N-Vortex Problem, Analytical Techniques. Springer.CrossRefGoogle Scholar
30. Novikov, E. A. 1976 Dynamics and statistics of a system of vortices. Sov. Phys. JETP 41, 937–943.Google Scholar
31. Novikov, E. A. & Sedov, Y. B. 1979 Vortex collapse. Sov. Phys. JETP 50 (2), 297–301.Google Scholar
32. Oliver, S. & Shkoller, S. 2001 The vortex blob method as a second-grade non-Newtonian fluid. Commun. Part. Diff. Equ. 26, 295–314.CrossRefGoogle Scholar
33. Onsager, L. 1949 Statistical hydrodynamics. Nuovo Cimento Suppl. 6, 279–289.CrossRefGoogle Scholar
34. Shashikanth, B. N. 2010 Dissipative -point-vortex models in the plane. J. Nonlinear Sci. 20, 81–103.CrossRefGoogle Scholar
35. Shkoller, S. 2001 Smooth global Lagrangian flow for the 2D Euler and second-grade fluid equations. Appl. Maths Lett. 14, 539–543.CrossRefGoogle Scholar
36. Synge, J. L. 1949 On the motion of three vortices. Can. J. Math. 1, 257–270.CrossRefGoogle Scholar
37. Watson, G. N. 2008 A Treatise on the Theory of Bessel Functions. Merchant Books.Google Scholar