Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-08T04:10:59.913Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability and low-frequency unsteadiness in a shock-induced laminar separation bubble

Published online by Cambridge University Press:  31 May 2016

Andrea Sansica ,
Neil D. Sandham  and
Zhiwei Hu
Andrea Sansica*
Affiliation:
Aerodynamics and Flight Mechanics Group, Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
Neil D. Sandham
Affiliation:
Aerodynamics and Flight Mechanics Group, Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
Zhiwei Hu
Affiliation:
Aerodynamics and Flight Mechanics Group, Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

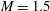Three-dimensional direct numerical simulations (DNS) of a shock-induced laminar separation bubble are carried out to investigate the flow instability and origin of any low-frequency unsteadiness. A laminar boundary layer interacting with an oblique shock wave at $M=1.5$ is forced at the inlet with a pair of monochromatic oblique unstable modes, selected according to local linear stability theory (LST) performed within the separation bubble. Linear stability analysis is applied to cases with marginal and large separation, and compared to DNS. While the parabolized stability equations approach accurately reproduces the growth of unstable modes, LST performs less well for strong interactions. When the modes predicted by LST are used to force the separated boundary layer, transition to deterministic turbulence occurs near the reattachment point via an oblique-mode breakdown. Despite the clean upstream condition, broadband low-frequency unsteadiness is found near the separation point with a peak at a Strouhal number of $0.04$, based on the separation bubble length. The appearance of the low-frequency unsteadiness is found to be due to the breakdown of the deterministic turbulence, filling up the spectrum and leading to broadband disturbances that travel upstream in the subsonic region of the boundary layer, with a strong response near the separation point. The existence of the unsteadiness is supported by sensitivity studies on grid resolution and domain size that also identify the region of deterministic breakdown as the source of white noise disturbances. The present contribution confirms the presence of low-frequency response for laminar flows, similarly to that found in fully turbulent interactions.

JFM classification

Boundary Layers: Boundary layer separation Compressible Flows: Compressible boundary layers Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 5 - 26
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ackeret, J., Feldmann, F. & Rott, N.1947 Investigation of compression shocks and boundary layers in gases moving at high speed. NACA Technical Memorandum 1113.Google Scholar
Alam, M. & Sandham, N. D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 410, 1–28.CrossRefGoogle Scholar
Arnal, D.1994 Boundary layer transition: predictions based on linear theory. AGARD Report 793.Google Scholar
Babinsky, H. & Harvey, J. K. 2011 Shock Wave–Boundary-Layer Interactions. Cambridge University Press.CrossRefGoogle Scholar
Balakumar, P. & Malik, M. R. 1992 Waves produced from a harmonic point source in a supersonic boundary-layer flow. J. Fluid Mech. 245, 229–247.CrossRefGoogle Scholar
Bertolotti, F. P.1991 Linear and nonlinear stability of boundary layers with streamwise varying properties. PhD thesis, Ohio State University.Google Scholar
Bertolotti, F. P. 1997 Response of the Blasius boundary layer to free-stream vorticity. Phys. Fluids 9, 2286–2299.CrossRefGoogle Scholar
Bertolotti, F. P., Herbert, T. & Spalart, P. R. 1992 Linear and nonlinear stability of the Blasius boundary layer. J. Fluid Mech. 242, 441–474.CrossRefGoogle Scholar
Borodulin, V. I., Kachanov, Y. S. & Roschektayev, A. P. 2011 Experimental detection of deterministic turbulence. J. Turbul. 12 (23), 1–34.CrossRefGoogle Scholar
Chang, C.-L., Malik, M. R., Erlebacher, G. & Hussaini, M. Y.1993 Linear and nonlinear PSE for compressible boundary layers. NASA ICASE Report 93–70.Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.CrossRefGoogle Scholar
Delery, J. & Marvin, J.1986 Shock-wave boundary layer interactions. AGARDograph 280. NATO Brussels.Google Scholar
Doerffer, P., Hirsch, C., Dussauge, J.-P., Babinsky, H. & Barakos, G. N. 2011 Unsteady Effects of Shock Wave Induced Separation. Cambridge University Press.CrossRefGoogle Scholar
Dolling, D. 2001 Fifty years of shock-wave/boundary-layer interaction research: what next? AIAA J. 39 (8), 1517–1531.CrossRefGoogle Scholar
Dupont, P., Haddad, C., Ardissone, J. P. & Debiève, J.-F. 2005 Space and time organization of a shock wave/turbulent boundary layer interaction. Aerosp. Sci. Technol. 9, 561–572.CrossRefGoogle Scholar
Dussauge, J.-P., Dupont, P. & Debiéve, J.-F. 2006 Unsteadiness in shock wave boundary layer interaction with separation. Aerosp. Sci. Technol. 10, 85–91.CrossRefGoogle Scholar
Eckert, E. R. G. 1955 Engineering relations for friction and heat transfer to surfaces in high velocity flow. J. Aeronaut. Sci. 22, 585–587.Google Scholar
El-Hady, N. M. 1991 Nonparallel instability of supersonic and hypersonic boundary layers. Phys. Fluids 3, 2164–2178.CrossRefGoogle Scholar
Erengil, M. E. & Dolling, D. S. 1991 Unsteady wave structure near separation at Mach 5 compression ramp interaction. AIAA J. 29, 728–735.CrossRefGoogle Scholar
Fasel, H., Thumm, A. & Bestek, H. 1993 Direct numerical simulation of transition in supersonic boundary layer: oblique breakdown. In Transitional and Turbulent Compressible Flows (ed. Kral, L. D. & Zang, T. A.), ASME-FED, vol. 151, pp. 77–92.Google Scholar
Ganapathisubramani, B., Clemens, N. & Dolling, D. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–394.CrossRefGoogle Scholar
Ganapathisubramani, B., Clemens, N. & Dolling, D. 2009 Low-frequency dynamics of shock-induced separation in a compression ramp interaction. J. Fluid Mech. 636, 397–436.CrossRefGoogle Scholar
Gaster, M. 1962 A note on the relation between temporally-increasing and spatially-increasing disturbances in hydrodynamic stability. J. Fluid Mech. 14, 222–224.CrossRefGoogle Scholar
Gaster, M. 1991 Stability of velocity profiles with reverse flow. In Instability, Transition and Turbulence, ICASE-Workshop, Berlin (ed. Hussaini, M. Y., Kumar, A. & Streett, C. L.), pp. 212–215. Springer.Google Scholar
Grilli, M., Schmid, P. J., Hickel, S. & Adams, N. A. 2012 Analysis of unsteady behaviour in shockwave turbulent boundary layer interaction. J. Fluid Mech. 700, 16–28.CrossRefGoogle Scholar
Hammond, D. A. & Redekopp, L. G. 1998 Local and global instability properties of separation bubbles. Eur. J. Mech. (B/Fluids) 17 (2), 317–328.Google Scholar
Hein, S.2005 Nonlinear nonlocal transition analysis. PhD thesis, Deutsches Zentrum für Aerodynamik und Strömungstechnik Göttingen/University of Stuttgart.Google Scholar
Herbert, T. 1993 Parabolized stability equations. AGARD CP 793 (1), 487–526.Google Scholar
Herbert, T. 1997 Parabolized stability equations. Annu. Rev. Fluid Mech. 29, 245–283.CrossRefGoogle Scholar
Herbert, T. & Bertolotti, F. P. 1987 Stability of nonparallel boundary layers. Bull. Am. Phys. Soc. 32, 2079.Google Scholar
Hu, Z., Morfey, C. L. & Sandham, N. D. 2006 Wall pressure and shear stress spectra from direct simulations of channel flow. AIAA J. 44 (7), 1541–1549.CrossRefGoogle Scholar
Kendall, J. M.1967 Boundary Layer Transition Study Group Meeting, vol. II, ed. W. D. McCauley. Tech. Rep. BSD-TR-67-213, US Air Force.Google Scholar
Kendall, J. M.1990 Boundary layer receptivity to freestream turbulence. AIAA Paper 90-1504.CrossRefGoogle Scholar
Klebanoff, P. S. 1971 Effect of free-stream turbulence on a laminar boundary layer. Bull. Am. Phys. Soc. 16, 1323.Google Scholar
Liepmann, H. W. 1946 The interaction between boundary layer and shock waves in transonic flow. J. Aeronaut. Sci. 13, 623–637.CrossRefGoogle Scholar
Macaraeg, M. G., Streett, C. L. & Hussaini, M. Y.1988 A spectral collocation solution to the compressible stability eigenvalue problem. NASA Technical Paper 2858.Google Scholar
Mack, L. M.1984 Boundary layer linear stability theory. Repository 709. AGARD.Google Scholar
Mack, L. M. & Herbert, T. 1995 Linear wave motion from concentrated harmonic sources in Blasius flow. In 33rd Aerospace Sciences Meeting and Exhibit, AIAA.Google Scholar
Malik, M. R. 1990 Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 86 (2), 376–413.CrossRefGoogle Scholar
Marxen, O., Lang, M., Rist, U. & Wagner, S. 2003 A combined experimental/numerical study of unsteady phenomena in a laminar separation bubble. Flow Turbul. Combust. 71, 133–146.CrossRefGoogle Scholar
Marxen, O., Rist, U. & Wagner, S. 2004 Effect of spanwise-modulated disturbances on transition in a separated boundary layer. AIAA J. 42, 937–944.CrossRefGoogle Scholar
Mayer, C. S., Von Terzi, D. A. & Fasel, H. F. 2011 Direct numerical simulation of complete transition to turbulence via oblique breakdown at Mach 3. J. Fluid Mech. 674, 5–42.CrossRefGoogle Scholar
Nikitin, N. 2008 On the rate of spatial predictability in near-wall turbulence. J. Fluid Mech. 614, 495–507.CrossRefGoogle Scholar
Pagella, A., Babucke, A. & Rist, U. 2004 Two-dimensional numerical investigations of small-amplitude disturbances in a boundary layer at Ma = 4. 8: compression corner versus impinging shock wave. Phys. Fluids 16, 2272–2281.CrossRefGoogle Scholar
Pagella, A., Rist, U. & Wagner, S. 2002 Numerical investigations of small-amplitude disturbances in a boundary layer with impinging shock wave at Ma = 4. 8. Phys. Fluids 14, 2088–2101.CrossRefGoogle Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at M = 2. 25. Phys. Fluids 18, 065113.CrossRefGoogle Scholar
Reed, L. H., Saric, W. S. & Arnal, D. 1996 Linear stability theory applied to boundary layers. Annu. Rev. Fluid Mech. 28, 389–428.CrossRefGoogle Scholar
Rist, U. 2004 Instability and Transition Mechanisms in Laminar Separation Bubbles. (RTO-AVT-VKI Lecture Series) , Von Karman Institute.Google Scholar
Rist, U. & Maucher, U. 1994 Direct numerical simulation of 2-D and 3-D instability waves in a laminar separation bubble. In Application of Direct and Large Eddy Simulation to Transition and Turbulence, Proceedings 74th Fluid Dynamics Symposium, Crete, Greece, 551, pp. 34-1–34-7. AGARD.Google Scholar
Robinet, J. Ch. 2007 Bifurcations in shock-wave/laminar-boundary-layer interaction: global instability approach. J. Fluid Mech. 579, 85–112.CrossRefGoogle Scholar
Sandham, N. D. & Adams, N. A. 1993 Numerical simulations of boundary-layer transition at Mach two. Appl. Sci. Res. 51, 371–375.CrossRefGoogle Scholar
Sandham, N. D., Adams, N. A. & Kleiser, L. 1995 Direct simulation of breakdown to turbulence following oblique instability waves in a supersonic boundary layer. Appl. Sci. Res. 54, 223–234.CrossRefGoogle Scholar
Sandham, N. D. & Kleiser, L. 1992 The late stages of transition to turbulence in channel flow. J. Fluid Mech. 245, 319–348.CrossRefGoogle Scholar
Sandham, N. D., Schülen, E., Wagner, A., Willems, S. & Steelant, J. 2014 Transitional shock-wave/boundary-layer interactions in hypersonic flow. J. Fluid Mech. 752, 349–382.CrossRefGoogle Scholar
Sansica, A.2015 Stability and unsteadiness of transitional shock-wave/boundary-layer interactions in supersonic flows. PhD thesis, University of Southampton.Google Scholar
Sansica, A., Sandham, N. D. & Hu, Z. 2014 Forced response of a laminar shock-induced separation bubble. Phys. Fluids 26, 093601.CrossRefGoogle Scholar
Settles, G. S. & Dodson, L. J.1991 Hypersonic shock/boundary-layer interaction database. NASA CR 177577.CrossRefGoogle Scholar
Settles, G. S. & Dodson, L. J. 1994 Supersonic and hypersonic shock/boundary layer interaction database. AIAA J. 32, 1377–1383.CrossRefGoogle Scholar
Settles, G. S. & Dolling, D. S.1990 Swept shock/boundary-layer interactions – tutorial and update. AIAA Paper 90-0375.CrossRefGoogle Scholar
Smiths, A. J. & Dussauge, J.-P. 2006 Turbulent Shear Layers in Supersonic Flow, 2nd edn. Springer.Google Scholar
Souverein, L. J., Dupont, P., Debiève, J.-F., Dussauge, J.-P., van Oudheusden, B. W. & Scarano, F.2009 Effect of interaction strength on the unsteady behavior of shock wave boundary layer interactions. AIAA Paper 2009-3715.CrossRefGoogle Scholar
Theofilis, V. 2003 Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 39, 249–315.CrossRefGoogle Scholar
Theofilis, V., Hein, S. & Dallmann, U. 2000 On the origins of unsteadiness and three- dimensionality in a laminar separation bubble. Phil. Trans. R. Soc. Lond. A 358, 3229–3246.CrossRefGoogle Scholar
Touber, E. & Sandham, N. D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23, 79–107.CrossRefGoogle Scholar
Welch, P. D. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15 (2), 70–73.CrossRefGoogle Scholar
Yao, Y., Krishnan, L., Sandham, N. D. & Roberts, G. T. 2007 The effect of Mach number on unstable disturbances in shock/boundary-layer interactions. Phys. Fluids 19, 054104.CrossRefGoogle Scholar
Young, A. D. 1989 Boundary Layers. (AIAA Education Series) , Blackwell Science.Google Scholar