Article contents
Input–output measures for model reduction and closed-loop control: application to global modes
Published online by Cambridge University Press: 06 October 2011
Abstract
Feedback control applications for flows with a large number of degrees of freedom require the reduction of the full flow model to a system with significantly fewer degrees of freedom. This model-reduction process is accomplished by Galerkin projections using a reduction basis composed of modal structures that ideally preserve the input–output behaviour between actuators and sensors and ultimately result in a stabilized compensated system. In this study, global modes are critically assessed as to their suitability as a reduction basis, and the globally unstable, two-dimensional flow over an open cavity is used as a test case. Four criteria are introduced to select from the global spectrum the modes that are included in the reduction basis. Based on these criteria, four reduced-order models are tested by computing open-loop (transfer function) and closed-loop (stability) characteristics. Even though weak global instabilities can be suppressed, the concept of reduced-order compensators based on global modes does not demonstrate sufficient robustness to be recommended as a suitable choice for model reduction in feedback control applications. The investigation also reveals a compelling link between frequency-restricted input–output measures of open-loop behaviour and closed-loop performance, which suggests the departure from mathematically motivated 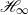 -measures for model reduction toward more physically based norms; a particular frequency-restricted input–output measure is proposed in this study which more accurately predicts the closed-loop behaviour of the reduced-order model and yields a stable compensated system with a markedly reduced number of degrees of freedom.
-measures for model reduction toward more physically based norms; a particular frequency-restricted input–output measure is proposed in this study which more accurately predicts the closed-loop behaviour of the reduced-order model and yields a stable compensated system with a markedly reduced number of degrees of freedom.
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 36
- Cited by


