Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T02:50:41.873Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of the viscous boundary layer perturbations on single-mode panel flutter at finite Reynolds numbers

Published online by Cambridge University Press:  10 August 2018

Vsevolod Bondarev Open the ORCID record for Vsevolod Bondarev [Opens in a new window]  and
Vasily Vedeneev Open the ORCID record for Vasily Vedeneev [Opens in a new window]
Vsevolod Bondarev
Affiliation:
Faculty of Mechanics and Mathematics, Lomonosov Moscow State University, Moscow, 119991, Russia
Vasily Vedeneev*
Affiliation:
Faculty of Mechanics and Mathematics, Lomonosov Moscow State University, Moscow, 119991, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Panel flutter is an aeroelastic instability of aircraft skin panels, which can lead to a reduction in service life and panel destruction. Despite the existence of many studies related to panel flutter, the influence of the boundary layer on the panel stability has been considered in only a few of them. Up to the present day, most papers on the boundary layer effect consider only a zero-pressure-gradient boundary layer over a flat plate. The only studies of a boundary layer of arbitrary form were conducted in our previous papers (Vedeneev, J. Fluid Mech., vol. 736, 2013, pp. 216–249 and Bondarev & Vedeneev, J. Fluid Mech., vol. 802, 2016, pp. 528–552), where the boundary layer was represented as an inviscid shear layer (the Reynolds number 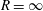$R=\infty$). In this paper we investigate the problem, taking viscosity into account, at large but finite Reynolds numbers. As before, we assume that the panel length is large and use Kulikovskii’s global instability criterion to analyse the panel eigenmodes and consider two different types of boundary layer profiles: a generalised convex profile and a profile with a generalised inflection point. Results show that viscous perturbations can, in general, have both stabilising and destabilising effects on the system, depending on the velocity and temperature profiles of the boundary layer and on its thickness. However, surprisingly, we prove that if the boundary layer yields a significant growth rate in the inviscid approximation, then the viscosity always produces an even larger growth rate.

JFM classification

Boundary Layers: Boundary Layers Boundary Layers: Boundary layer stability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 852 , 10 October 2018 , pp. 578 - 601
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alder, M. 2015 Development and validation of a fluid structure solver for transonic panel flutter. AIAA J. 53 (12), 3509–3521.Google Scholar
Alder, M. 2016 Nonlinear dynamics of pre-stressed panels in low supersonic turbulent flow. AIAA J. 54 (11), 1–15.Google Scholar
Bolotin, V. V. 1963 Nonconservative Problems of the Theory of Elastic Stability. Pergamon.Google Scholar
Bondarev, V. O. & Vedeneev, V. V. 2016 Short-wave instability of elastic plates in supersonic flow in the presence of the boundary layer. J. Fluid Mech. 802, 528–552.Google Scholar
Bondarev, V. O. & Vedeneev, V. V. 2017 Flutter of infinite elastic plates in the boundary-layer flow at finite Reynolds numbers. Fluid Dyn. 52 (6), 797–814.Google Scholar
Dowell, E. H. 1974 Aeroelasticity of Plates and Shells. Noordhoff International Publishing.Google Scholar
Dowell, E. H. 1971 Generalized aerodynamic forces on a flexible plate undergoing transient motion in a shear flow with an application to panel flutter. AIAA J. 9 (5), 834–841.Google Scholar
Dowell, E. H. 1973 Aerodynamic boundary layer effect on flutter and damping of plates. J. Aircraft 10 (12), 734–738.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Gaponov, S. A. & Maslov, A. A. 1980 Development of Perturbations in Compressible Flows. Nauka (in Russian).Google Scholar
Gaspers, P. A. Jr, Muhlstein, L. Jr & Petroff, D. N. 1970 Further results on the influence of the turbulent boundary layer on panel flutter. NASA TN D-5798.Google Scholar
Hashimoto, A., Aoyama, T. & Nakamura, Y. 2009 Effect of turbulent boundary layer on panel flutter. AIAA J. 47 (12), 2785–2791.Google Scholar
Miles, J. W. 1959 On panel flutter in the presence of a boundary layer. J. Aerosp. Sci. 26 (2), 81–93, 107.Google Scholar
Muhlstein, L. Jr, Gaspers, P. A. Jr & Riddle, D. W. 1968 An experimental study of the influence of the turbulent boundary layer on panel flutter. NASA TN D-4486.Google Scholar
Kulikovskii, A. G. 1966 On the stability of homogeneous states. J. Appl. Math. Mech. 30 (1), 180–187.Google Scholar
Lees, L. & Lin, C. C.1946 Investigation of the stability of the laminar boundary layer in a compressible fluid. NACA TN 1115.Google Scholar
Novichkov, Yu. N. 1978 Flutter of plates and shells. In Advances in Science and Technology. Mechanics of Deformable Solids, vol. 11, pp. 67–122. VINITI Press (in Russian).Google Scholar
Schlichting, H. 1960 Boundary Layer Theory. McGraw-Hill.Google Scholar
Vedeneev, V. V. 2005 Flutter of a wide strip plate in a supersonic gas flow. Fluid Dyn. 5, 805–817.Google Scholar
Vedeneev, V. V. 2012 Panel flutter at low supersonic speeds. J. Fluids Struct. 29, 79–96.Google Scholar
Vedeneev, V. V. 2013 Interaction of panel flutter with inviscid boundary layer instability in supersonic flow. J. Fluid Mech. 736, 216–249.Google Scholar
Vedeneev, V. V. 2016 On the application of the asymptotic method of global instability in aeroelasticity problems. Proc. Steklov Inst. Math. 295, 292–320.Google Scholar
Visbal, M. 2014 Viscous and inviscid interactions of an oblique shock with a flexible panel. J. Fluids Struct. 48, 27–45.Google Scholar