Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T04:20:41.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of initial turbulence level on the flow and sound fields of a subsonic jet at a diameter-based Reynolds number of 105

Published online by Cambridge University Press:  18 May 2012

C. Bogey ,
O. Marsden  and
C. Bailly
C. Bogey*
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, UMR CNRS 5509, Ecole Centrale de Lyon, Université de Lyon, 69134 Ecully CEDEX, France
O. Marsden
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, UMR CNRS 5509, Ecole Centrale de Lyon, Université de Lyon, 69134 Ecully CEDEX, France
C. Bailly
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, UMR CNRS 5509, Ecole Centrale de Lyon, Université de Lyon, 69134 Ecully CEDEX, France Institut Universitaire de France, 103 boulevard Saint-Michel, 75005 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Five isothermal round jets at Mach number 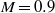and Reynolds number 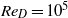originating from a pipe nozzle are computed by large-eddy simulations to investigate the effects of initial turbulence on flow development and noise generation. In the pipe, the boundary layers are untripped in the first case and tripped numerically in the four others in order to obtain, at the exit, mean velocity profiles similar to a Blasius laminar profile of momentum thickness equal to 1.8 % of the jet radius, yielding Reynolds number 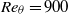, and peak turbulence levels 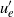around 0, 3 %, 6 %, 9 % or 12 % of the jet velocity 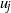. As the initial turbulence intensity increases, the shear layers develop more slowly with much lower root-mean-square (r.m.s.) fluctuating velocities, and the jet potential cores are longer. Velocity disturbances downstream of the nozzle exit also exhibit different structural characteristics. For low 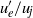, they are dominated by the first azimuthal modes 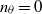, 1 and 2, and show significant skewness and intermittency. The growth of linear instability waves and a first stage of vortex pairings occur in the shear layers for 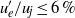. For higher 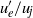, three-dimensional features and high azimuthal modes prevail, in particular close to the nozzle exit where the wavenumbers naturally found in turbulent wall-bounded flows clearly appear. Concerning the sound fields, strong broadband components mainly associated with mode 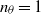are noticed around the pairing frequency for the untripped jet. With rising 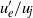, however, they become weaker, and the noise levels decrease asymptotically down to those measured for jets at 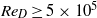, which are likely to be initially turbulent and to emit negligible vortex-pairing noise. These results correspond well to experimental observations, made separately for either mixing layers, jet flow or sound fields.

JFM classification

Boundary Layers: Free shear layers Acoustics: Jet noise Turbulent Flows: Shear layer turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 701 , 25 June 2012 , pp. 352 - 385
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ahuja, K. K., Tester, B. J. & Tanna, H. K. 1987 Calculation of far field jet noise spectra from near field measurements with true source location. J. Sound Vib. 116 (3), 415–426.CrossRefGoogle Scholar
2. Arakeri, V. H., Krothapalli, A., Siddavaram, V., Alkislar, M. B. & Lourenco, L. 2003 On the use of microjets to suppress turbulence in a Mach 0.9 axisymmetric jet. J. Fluid Mech. 490, 75–98.CrossRefGoogle Scholar
3. Bailly, C. & Bogey, C. 2004 Contributions of CAA to jet noise research and prediction. Intl J. Comput. Fluid Dyn. 18 (6), 481–491.CrossRefGoogle Scholar
4. Batt, R. G. 1975 Some measurements on the effect of tripping the two-dimensional shear layer. AIAA J. 13 (2), 245–247.CrossRefGoogle Scholar
5. Bell, J. H. & Mehta, R. D. 1990 Development of a two-stream mixing layer from tripped and untripped boundary layers. AIAA J. 28 (12), 2034–2042.CrossRefGoogle Scholar
6. Berland, J., Bogey, C., Marsden, O. & Bailly, C. 2007 High-order, low dispersive and low dissipative explicit schemes for multi-scale and boundary problems. J. Comput. Phys. 224 (2), 637–662.CrossRefGoogle Scholar
7. Bogey, C. & Bailly, C. 2002 Three-dimensional non reflective boundary conditions for acoustic simulations: far-field formulation and validation test cases. Acta Acust. 88 (4), 463–471.Google Scholar
8. Bogey, C. & Bailly, C. 2004 A family of low dispersive and low dissipative explicit schemes for flow and noise computations. J. Comput. Phys. 194 (1), 194–214.CrossRefGoogle Scholar
9. Bogey, C. & Bailly, C. 2006a Large Eddy Simulations of transitional round jets: influence of the Reynolds number on flow development and energy dissipation. Phys. Fluids 18 (6), 065101.CrossRefGoogle Scholar
10. Bogey, C. & Bailly, C. 2006b Large eddy simulations of round jets using explicit filtering with/without dynamic Smagorinsky model. Intl J. Heat Fluid Flow 27 (4), 603–610.CrossRefGoogle Scholar
11. Bogey, C. & Bailly, C. 2006c Investigation of downstream and sideline subsonic jet noise using large eddy simulation. Theor. Comput. Fluid Dyn. 20 (1), 23–40.CrossRefGoogle Scholar
12. Bogey, C. & Bailly, C. 2007 An analysis of the correlations between the turbulent flow and the sound pressure field of subsonic jets. J. Fluid Mech. 583, 71–97.CrossRefGoogle Scholar
13. Bogey, C. & Bailly, C. 2009 Turbulence and energy budget in a self-preserving round jet: direct evaluation using large-eddy simulation. J. Fluid Mech. 627, 129–160.CrossRefGoogle Scholar
14. Bogey, C. & Bailly, C. 2010 Influence of nozzle-exit boundary-layer conditions on the flow and acoustic fields of initially laminar jets. J. Fluid Mech. 663, 507–539.CrossRefGoogle Scholar
15. Bogey, C., Bailly, C. & Juvé, D. 2003 Noise investigation of a high subsonic, moderate Reynolds number jet using a compressible LES. Theor. Comput. Fluid Dyn. 16 (4), 273–297.CrossRefGoogle Scholar
16. Bogey, C., Barré, S. & Bailly, C. 2008 Direct computation of the noise generated by subsonic jets originating from a straight pipe nozzle. Intl J. Aeroacoust. 7 (1), 1–22.CrossRefGoogle Scholar
17. Bogey, C., Barré, S., Fleury, V., Bailly, C. & Juvé, D. 2007 Experimental study of the spectral properties of near-field and far-field jet noise. Intl J. Aeroacoust. 6 (2), 73–92.CrossRefGoogle Scholar
18. Bogey, C., Barré, S., Juvé, D. & Bailly, C. 2009a Simulation of a hot coaxial jet: direct noise prediction and flow-acoustics correlations. Phys. Fluids 21 (3), 035105.CrossRefGoogle Scholar
19. Bogey, C., de Cacqueray, N. & Bailly, C. 2009b A shock-capturing methodology based on adaptative spatial filtering for high-order nonlinear computations. J. Comput. Phys. 228 (5), 1447–1465.CrossRefGoogle Scholar
20. Bogey, C., de Cacqueray, N. & Bailly, C. 2011 Finite differences for coarse azimuthal discretization and for reduction of effective resolution near origin of cylindrical flow equations. J. Comput. Phys. 230 (4), 1134–1146.CrossRefGoogle Scholar
21. Bogey, C., Marsden, O. & Bailly, C. 2011a Large-eddy simulation of the flow and acoustic fields of a Reynolds number subsonic jet with tripped exit boundary layers. Phys. Fluids 23 (3), 035104.CrossRefGoogle Scholar
22. Bogey, C., Marsden, O. & Bailly, C. 2011b On the spectra of nozzle-exit velocity disturbances in initially nominally turbulent, transitional jets. Phys. Fluids 23 (9), 091702.CrossRefGoogle Scholar
23. Bogey, C., Marsden, O. & Bailly, C. 2012 Flow and sound fields of initially tripped jets at Reynolds numbers ranging from 25,000 to 200,000. AIAA Paper 2012-1172. Meeting.CrossRefGoogle Scholar
24. Bridges, J. E. & Hussain, A. K. M. F. 1987 Roles of initial conditions and vortex pairing in jet noise. J. Sound Vib. 117 (2), 289–311.CrossRefGoogle Scholar
25. Briggs, D. A., Ferziger, J. H., Koseff, J. R. & Monismith, S. G. 1996 Entrainment in a shear-free turbulent mixing layer. J. Fluid Mech. 310, 215–241.CrossRefGoogle Scholar
26. Browand, F. K. & Latigo, B. O. 1979 Growth of the two-dimensional mixing layer from a turbulent and nonturbulent boundary layer. Phys. Fluids 22 (6), 1011–1019.CrossRefGoogle Scholar
27. Browand, F. K. & Troutt, C. D. 1980 A note on spanwise structure in the two-dimensional mixing layer. J. Fluid Mech. 97 (4), 771–781.CrossRefGoogle Scholar
28. Brown, G. L. & Roshko, A. 1974 Density effect and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.CrossRefGoogle Scholar
29. Camussi, R. & Guj, G. 1999 Experimental analysis of intermittent coherent structures in the near field of a high Re turbulent jet flow. Phys. Fluids 11 (2), 423–431.CrossRefGoogle Scholar
30. Cavalieri, A. V. G., Jordan, P., Gervais, Y., Wei, M. & Freund, J. B. 2010 Intermittent sound generation and its control in a free-shear flow. Phys. Fluids 22 (11), 115113.CrossRefGoogle Scholar
31. Chandrsuda, C., Mehta, R. D., Weir, A. D. & Bradshaw, P. 1978 Effect of free stream turbulence on large structure in turbulent mixing layer. J. Fluid Mech. 85 (4), 693–704.CrossRefGoogle Scholar
32. Chevray, R. & Tutu, N. K. 1978 Intermittency and preferential transport of heat in a round jet. J. Fluid Mech. 88 (1), 133–160.CrossRefGoogle Scholar
33. Cohen, J. & Wygnanski, I. 1987 The evolution of instabilities in the axisymmetric jet. Part 1. The linear growth of disturbances near the nozzle. J. Fluid Mech. 176, 191–219.CrossRefGoogle Scholar
34. Colonius, T. & Lele, S. K. 2004 Computational aeroacoustics: progress on nonlinear problems of sound generation. Prog. Aero. 40, 345–416.CrossRefGoogle Scholar
35. Colonius, T., Lele, S. K. & Moin, P. 1997 Sound generation in a mixing layer. J. Fluid Mech. 330, 375–409.CrossRefGoogle Scholar
36. Crighton, D. G. 1981 Acoustics as a branch of fluid mechanics. J. Fluid Mech. 106, 261–298.CrossRefGoogle Scholar
37. Crow, S. C. & Champagne, F. H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48, 547–591.CrossRefGoogle Scholar
38. Davies, P. O. A. L., Fisher, M. J. & Barratt, M. J. 1963 The characteristics of the turbulence in the mixing region of a round jet. J. Fluid Mech. 15, 337–367.CrossRefGoogle Scholar
39. Domaradzki, J. A. & Yee, P. P. 2000 The subgrid-scale estimation model for high Reynolds number turbulence. Phys. Fluids 12 (1), 193–196.CrossRefGoogle Scholar
40. Eggels, J. G. M., Unger, F., Weiss, M. H., Westerweel, J., Adrian, R. J., Friedrich, R. & Nieuwstadt, F. T. M. 1994 Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–209.CrossRefGoogle Scholar
41. Fleury, V., Bailly, C., Jondeau, E., Michard, M. & Juvé, D. 2008 Space-time correlations in two subsonic jets using dual-PIV measurements. AIAA J. 46 (10), 2498–2509.CrossRefGoogle Scholar
42. Freund, J. B. 2001 Noise sources in a low-Reynolds-number turbulent jet at Mach 0.9. J. Fluid Mech. 438, 277–305.CrossRefGoogle Scholar
43. Ghosh, S., Foysi, H. & Friedrich, R. 2010 Compressible turbulent channel and pipe flow: similarities and differences. J. Fluid Mech. 648, 155–181.CrossRefGoogle Scholar
44. Grosche, F.-R. 1974 Distributions of sound source intensities in subsonic and supersonic jets. AGARD-CP-131, 4-1 to 4-10.Google Scholar
45. Gutmark, E. & Ho, C.-M. 1983 Preferred modes and the spreading rates of jets. Phys. Fluids 26 (10), 2932–2938.CrossRefGoogle Scholar
46. Harper-Bourne, M. 2010 Jet noise measurements: past and present. Intl J. Aeroacoust. 9 (4 & 5), 559–588.CrossRefGoogle Scholar
47. Hileman, J. I., Thurow, B. S., Caraballo, E. J. & Samimy, M. 2005 Large-scale structure evolution and sound emission in high speed jets: real-time visualization with simultaneous acoustic measurements. J. Fluid Mech. 544, 277–307.CrossRefGoogle Scholar
48. Hill, W. G., Jenkins, R. C. & Gilbert, B. L. 1976 Effects of the initial boundary-layer state on turbulent jet mixing. AIAA J. 14 (11), 1513–1514.CrossRefGoogle Scholar
49. Ho, C.-M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 23 (3), 365–424.CrossRefGoogle Scholar
50. Husain, Z. D. & Hussain, A. K. M. F. 1979 Axisymmetric mixing layer: influence of the initial and boundary conditions. AIAA J. 17 (1), 48–55.CrossRefGoogle Scholar
51. Hussain, A. K. M. F. 1983 Coherent structures–reality and myth. Phys. Fluids 26 (10), 2816–2850.CrossRefGoogle Scholar
52. Hussain, A. K. M. F. & Husain, Z. D. 1980 Turbulence structure in the axisymmetric free mixing layer. AIAA J. 18 (12), 1462–1469.CrossRefGoogle Scholar
53. Hussain, A. K. M. F & Zedan, M. F. 1978a Effects of the initial condition on the axisymmetric free shear layer: Effects of the initial momentum thickness. Phys. Fluids 21 (7), 1100–1112.CrossRefGoogle Scholar
54. Hussain, A. K. M. F. & Zedan, M. F. 1978b Effects of the initial condition on the axisymmetric free shear layer: Effects of the initial fluctuation level. Phys. Fluids 21 (9), 1475–1481.CrossRefGoogle Scholar
55. Jones, B. G., Planchon, H. P. & Hammersley, R. J. 1973 Turbulent correlation measurements in a two-stream mixing layer. AIAA J. 11 (8), 1146–1150.CrossRefGoogle Scholar
56. Juvé, D. & Sunyach, M. 1981 Near and far field azimuthal correlations for excited jets. AIAA Paper 81-2011.CrossRefGoogle Scholar
57. Juvé, D., Sunyach, M. & Comte-Bellot, G. 1980 Intermittency of the noise emission in subsonic cold jets. J. Sound Vib. 71 (3), 319–332.CrossRefGoogle Scholar
58. Kim, J. & Choi, H. 2009 Large eddy simulation of a circular jet: effect of inflow conditions on the near field. J. Fluid Mech. 620, 383–411.CrossRefGoogle Scholar
59. Lau, J. C., Morris, P. J. & Fisher, M. J. 1979 Measurements in subsonic and supersonic free jets using a laser velocimeter. J. Fluid Mech. 93 (1), 1–27.CrossRefGoogle Scholar
60. Lepicovsky, J. & Brown, W. H. 1989 Effects of nozzle exit boundary-layer conditions on excitability of heated free jets. AIAA J. 27 (6), 712–718.CrossRefGoogle Scholar
61. Lilley, G. M. 1994 Jet noise classical theory and experiments. In Aeroacoustics of Flight Vehicles (ed. Hubbard, H. H. ). Noise Sources , vol. 1. pp. 211–289. Acoustical Society of America.Google Scholar
62. Lush, P. A. 1971 Measurements of subsonic jet noise and comparison with theory. J. Fluid Mech. 46 (3), 477–500.CrossRefGoogle Scholar
63. Maestrello, L. 1976 Two points correlations of sound pressure in the far field of a jet: Experiment. Tech. Mem. 72835. NASA-Langley Research Center.CrossRefGoogle Scholar
64. Maestrello, L. & McDaid, E. 1971 Acoustic characteristics of a high-subsonic jet. AIAA J. 9 (6), 1058–1066.CrossRefGoogle Scholar
65. Mathis, R., Marusic, I., Hutchins, N. & Sreenivasan, K. R. 2011 The relationship between the velocity skewness and the amplitude modulation of the small scale by the large scale in turbulent boundary layers. Phys. Fluids 23 (12), 121702.CrossRefGoogle Scholar
66. Michalke, A. 1984 Survey on jet instability theory. Prog. Aerosp. Sci. 21, 159–199.CrossRefGoogle Scholar
67. Mitchell, B. E., Lele, S. K. & Moin, P. 1999 Direct computation of the sound generated by vortex pairing in an axisymmetric jet. J. Fluid Mech. 383, 113–142.CrossRefGoogle Scholar
68. Mohseni, K. & Colonius, T. 2000 Numerical treatment of polar coordinate singularities. J. Comput. Phys. 157 (2), 787–795.CrossRefGoogle Scholar
69. Mollo-Christensen, E., Kolpin, M. A. & Martucelli, J. R. 1964 Experiments on jet flows and jet noise far-field spectra and directivity patterns. J. Fluid Mech. 18, 285–301.CrossRefGoogle Scholar
70. Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.CrossRefGoogle Scholar
71. Morris, P. J. 1976 The spatial viscous instability of axisymmetric jets. J. Fluid Mech. 77 (3), 511–529.CrossRefGoogle Scholar
72. Morris, P. J. 1983 Viscous stability of compressible axisymmetric jets. AIAA J. 21 (4), 481–482.CrossRefGoogle Scholar
73. Morris, P. J. & Zaman, K. B. M. Q. 2009 Velocity measurements in jets with application to noise source modelling. J. Sound Vib. 329 (4), 394–414.CrossRefGoogle Scholar
74. Papamoschou, D. & Debiasi, M. 2001 Directional suppression of noise from a high-speed jet. AIAA J. 39 (3), 380–387.CrossRefGoogle Scholar
75. Raman, G., Rice, E. J. & Reshotko, E. 1994 Mode spectra of natural disturbances in a circular jet and the effect of acoustic forcing. Exp. Fluids 17, 415–426.CrossRefGoogle Scholar
76. Raman, G., Zaman, K. B. M. Q. & Rice, E. J. 1989 Initial turbulence effect on jet evolution with and without tonal excitation. Phys. Fluids A 1 (7), 1240–1248.CrossRefGoogle Scholar
77. Russ, S. & Strykowski, P. J. 1993 Turbulent structure and entrainment in heated jets: The effect of initial conditions. Phys. Fluids A 5 (12), 3216–3225.CrossRefGoogle Scholar
78. Suzuki, T. & Colonius, T. 2007 Instability waves in a subsonic round jet detected using a near-field phased microphone array. J. Fluid Mech. 565, 197–226.CrossRefGoogle Scholar
79. Tam, C. K. W. & Dong, Z. 1996 Radiation and outflow boundary conditions for direct computation of acoustic and flow disturbances in a non-uniform mean flow. J. Comput. Acoust. 4 (2), 175–201.CrossRefGoogle Scholar
80. Tanna, H. K. 1977 An experimental study of jet noise. Part I: Turbulent mixing noise. J. Sound Vib. 50 (3), 405–428.CrossRefGoogle Scholar
81. Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
82. Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141–162.CrossRefGoogle Scholar
83. Visbal, M. R. & Rizzetta, D. P. 2002 Large-Eddy Simulation on curvilinear grids using compact differencing and filtering schemes. Trans. ASME: J. Fluids Engng 124 (4), 836–847.Google Scholar
84. Wang, M., Freund, J. B. & Lele, S. K. 2006 Computational prediction of flow-generated sound. Annu. Rev. Fluid Mech. 38, 483–512.CrossRefGoogle Scholar
85. Winant, C. D. & Browand, F. K. 1974 Vortex pairing: the mechanism od turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 63 (2), 237–255.CrossRefGoogle Scholar
86. Wygnanski, I., Oster, D., Fiedler, H. & Dziomba, B. 1979 On the perseverance of a quasi-two-dimensional eddy-structure in a turbulent mixing layer. J. Fluid Mech. 93 (2), 325–335.CrossRefGoogle Scholar
87. Xu, G. & Antonia, R. A. 2002 Effects of different initial conditions on a turbulent free jet. Exp. Fluids 33, 677–683.CrossRefGoogle Scholar
88. Zaman, K. B. M. Q. 1985a Far-field noise of subsonic jet under controlled excitation. J. Fluid Mech. 152, 83–111.CrossRefGoogle Scholar
89. Zaman, K. B. M. Q. 1985b Effect of initial condition on subsonic jet noise. AIAA J. 23, 1370–1373.CrossRefGoogle Scholar
90. Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1980 Vortex pairing in a circular jet under controlled excitation. Part 1. General jet response. J. Fluid Mech. 101 (3), 449–491.CrossRefGoogle Scholar

Bogey et al.

Snapshots in the (z, r) plane of vorticity norm obtained in the shear layer just downstream of the nozzle lip for jets at Reynolds number 105 with peak exit turbulence intensities of 0%, 3%, 6%, 9% and 12% (Jet0%, Jet3%, Jet6%, Jet9% and Jet12%, respectively). The colour scale ranges up to the level of 21uj/r0 (uj is the jet velocity, r0 is the nozzle radius).

Download Bogey et al.(Video)
Video 3.1 MB

Bogey et al.

Snapshots in the (z, r) plane of vorticity norm obtained in the shear layer just downstream of the nozzle lip for jets at Reynolds number 105 with peak exit turbulence intensities of 0%, 3%, 6%, 9% and 12% (Jet0%, Jet3%, Jet6%, Jet9% and Jet12%, respectively). The colour scale ranges up to the level of 21uj/r0 (uj is the jet velocity, r0 is the nozzle radius).

Download Bogey et al.(Video)
Video 9.3 MB

Bogey et al.

Snapshots in the (z, r ) plane of vorticity norm obtained up to z = 10r0 in jets at Reynolds number 105 with peak exit turbulence intensities of 0%, 3%, 6%, 9% and 12%. The colour scale ranges up to the level of 13uj /r0.

Download Bogey et al.(Video)
Video 4.7 MB

Bogey et al.

Snapshots in the (z, r ) plane of vorticity norm obtained up to z = 10r0 in jets at Reynolds number 105 with peak exit turbulence intensities of 0%, 3%, 6%, 9% and 12%. The colour scale ranges up to the level of 13uj /r0.

Download Bogey et al.(Video)
Video 18 MB

Bogey et al.

Snapshots in the (z, r ) plane of vorticity norm obtained up to z = 25r 0 in jets at Reynolds number 105 with peak exit peak turbulence intensities of 0%, 3%, 6%, 9% and 12%. The colour scale ranges up to the level of 5uj /r 0.

Download Bogey et al.(Video)
Video 4.5 MB

Bogey et al.

Snapshots in the (z, r ) plane of vorticity norm obtained up to z = 25r 0 in jets at Reynolds number 105 with peak exit peak turbulence intensities of 0%, 3%, 6%, 9% and 12%. The colour scale ranges up to the level of 5uj /r 0.

Download Bogey et al.(Video)
Video 17.1 MB

Bogey et al.

Snapshots in the (z, r ) plane of vorticity norm and fluctuating pressure obtained for jets at Reynolds number 105 with peak exit turbulence intensities of 0%, 3%, 6%, 9% and 12%. The colour scales range up to the level of 6uj /r 0 for vorticity, and from −65 to 65 Pa for pressure.

Download Bogey et al.(Video)
Video 10.1 MB

Bogey et al.

Snapshots in the (z, r ) plane of vorticity norm and fluctuating pressure obtained for jets at Reynolds number 105 with peak exit turbulence intensities of 0%, 3%, 6%, 9% and 12%. The colour scales range up to the level of 6uj /r 0 for vorticity, and from −65 to 65 Pa for pressure.

Download Bogey et al.(Video)
Video 41.7 MB