Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T12:47:14.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial collapse of liquid rings

Published online by Cambridge University Press:  07 February 2013

Baptiste Darbois Texier ,
Keyvan Piroird ,
David Quéré  and
Christophe Clanet
Baptiste Darbois Texier
Affiliation:
PMMH, UMR 7636 CNRS, ESPCI, Université Paris 6, Université Paris 7, 75005 Paris, France Ladhyx, UMR 7646 CNRS, École Polytechnique, 91128 Palaiseau, France
Keyvan Piroird*
Affiliation:
PMMH, UMR 7636 CNRS, ESPCI, Université Paris 6, Université Paris 7, 75005 Paris, France Ladhyx, UMR 7646 CNRS, École Polytechnique, 91128 Palaiseau, France
David Quéré
Affiliation:
PMMH, UMR 7636 CNRS, ESPCI, Université Paris 6, Université Paris 7, 75005 Paris, France Ladhyx, UMR 7646 CNRS, École Polytechnique, 91128 Palaiseau, France
Christophe Clanet
Affiliation:
PMMH, UMR 7636 CNRS, ESPCI, Université Paris 6, Université Paris 7, 75005 Paris, France Ladhyx, UMR 7646 CNRS, École Polytechnique, 91128 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

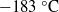Liquid rings can be generated in the Leidenfrost state using liquid oxygen of low boiling point ($- 183~\textdegree \mathrm{C} $) and high magnetic susceptibility, allowing one to ‘sculpt’ the liquid into a ring shape using an annular magnet. When the magnetic field is turned off, the ring shrinks back into a puddle with a constant acceleration. A potential flow approach accurately describes the dynamics of closure with an equation reminiscent of the Rayleigh–Plesset equation for the collapse of transient cavities.

JFM classification

Drops and Bubbles: Drops and Bubbles Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , R3
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aussillous, P. & Quéré, D. 2004 Shapes of rolling liquid drops. J. Fluid Mech. 512, 133–151.Google Scholar
Bartolo, D., Josserand, C. & Bonn, D. 2006 Singular jets and bubbles in drop impact. Phys. Rev. Lett. 96, 124501.Google Scholar
Bembenek, S. D. 2006 Calculations of the surface tension of oxygen using molecular-dynamics simulations. J. Chem. Phys. 124, 014709.Google Scholar
Bergmann, R., van der Meer, D., Gekle, S., van der Bos, A. & Lohse, D. 2009 Controlled impact of a disk on a water surface: cavity dynamics. J. Fluid Mech. 633, 381–409.Google Scholar
Brown, R. A. & Scriven, L. E. 1980 The shape and stability of rotating liquid drops. Proc. R. Soc. Lond. A 371, 331–357.Google Scholar
Chen, Y.-J. & Steen, P. H. 1997 Dynamics of inviscid capillary breakup: collapse and pinchoff of a film bridge. J. Fluid Mech. 341, 245–267.Google Scholar
Day, R. F., Hinch, E. J. & Lister, J. R. 1998 Self-similar capillary pinchoff of an inviscid fluid. Phys. Rev. Lett. 80, 704–707.Google Scholar
Duclaux, V., Caillé, F., Duez, C., Ybert, C., Bocquet, L. & Clanet, C. 2007 Dynamics of transient cavities. J. Fluid Mech. 591, 1–19.Google Scholar
Eggers, J. 2011 The subtle dynamics of liquid sheets. J. Fluid Mech. 672, 1–4.Google Scholar
Gekle, S., van der Meer, D., Snoeijer, J. H. & Lohse, D. 2009 Approach to universality in axisymmetric bubble pinch-off. Phys. Rev. E 80, 036305.Google Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2005 Gouttes, Bulles, Perles et Ondes. Belin, collection Échelles.Google Scholar
Hilgenfeldt, S., Brenner, M. P., Grossmann, S. & Lohse, D. 1998 Analysis of Rayleigh–Plesset dynamics for sonoluminescing bubbles. J. Fluid Mech. 365, 171–204.Google Scholar
Kojima, M., Hinch, E. J. & Acrivos, A. 1984 The formation and expansion of a toroidal drop moving in a viscous fluid. Phys. Fluids 27, 19–32.Google Scholar
Leppinen, D. & Lister, J. R. 2003 Capillary pinch-off in inviscid fluids. Phys. Fluids 15, 568–578.Google Scholar
Lide, D. R. 2010 CRC Handbook of Chemistry and Physics, 90th edn. CRC Press/Taylor and Francis.Google Scholar
McGraw, J. D., Li, J., Tran, D. L., Shi, A. C. & Dalnoki-Veress, K. 2010 Plateau-Rayleigh instability in a torus: formation and breakup of a polymer ring. Soft Matt. 6, 1258–1262.CrossRefGoogle Scholar
Nguyen, T. D., Fuentes-Cabrera, M., Fowlkes, J. D., Diez, J. A., González, A. G., Kondic, L. & Rack, P. D. 2012 Competition between collapse and breakup in nanometre-sized thin rings using molecular dynamics and continuum modelling. Langmuir 28, 13960–13967.Google Scholar
Pairam, E. & Fernandez-Nieves, A. 2009 Generation and stability of toroidal droplets in a viscous liquid. Phys. Rev. Lett. 102, 234501.Google Scholar
Piroird, K., Clanet, C. & Quéré, D. 2012a Magnetic control of Leidenfrost drops. Phys. Rev. E 85, 056311.Google Scholar
Piroird, K, Darbois Texier, B., Clanet, C. & Quéré, D. 2012 b Shaping and capturing drops with a magnet. Phys. Fluids  (under consideration for publication).Google Scholar
Plateau, J. A. F. 1863 Experimental and theoretical researches on the figures of equilibrium of a liquid mass withdrawn from the action of gravity. In Annual Report of the Board of Regents of the Smithsionian Institution, pp. 270–285.Google Scholar
Plesset, M. S. & Prosperetti, A. 1977 Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 9, 145–185.Google Scholar
Sostarecz, M. C. & Belmonte, A. 2003 Motion and shape of a viscoelastic drop falling through a viscous fluid. J. Fluid Mech. 497, 235–252.Google Scholar
Worthington, M. A. 1879 On the spontaneous segmentation of a liquid annulus. Proc. R. Soc. Lond. 30, 49–60.Google Scholar
Yao, Z. & Bowick, M. J. 2011 The shrinking instability of toroidal liquid droplets in the Stokes flow regime. Eur. Phys. J. E 34, 1–6.Google Scholar

Darbois Texier et al. supplementary movie

Top view of a collapsing liquid oxygen ring, of initial radius Ro = 4 mm and initial width ao = 2

Download Darbois Texier et al. supplementary movie(Video)
Video 1.4 MB