Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T14:08:43.837Z Has data issue: false hasContentIssue false
  • English
  • Français

The impact of dynamic roughness elements on marginally separated boundary layers

Published online by Cambridge University Press:  19 September 2018

P. Servini Open the ORCID record for P. Servini [Opens in a new window] ,
F. T. Smith  and
A. P. Rothmayer
P. Servini
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK
F. T. Smith*
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK
A. P. Rothmayer
Affiliation:
Department of Aerospace Engineering, Iowa State University, Ames, Iowa 50011, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It has been shown experimentally that dynamic roughness elements – small bumps embedded within a boundary layer, oscillating at a fixed frequency – are able to increase the angle of attack at which a laminar boundary layer will separate from the leading edge of an airfoil (Grager et al., in 6th AIAA Flow Control Conference, 2012, pp. 25–28). In this paper, we attempt to verify that such an increase is possible by considering a two-dimensional dynamic roughness element in the context of marginal separation theory, and suggest the mechanisms through which any increase may come about. We will show that a dynamic roughness element can increase the value of 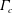$\unicode[STIX]{x1D6E4}_{c}$ as compared to the clean airfoil case; 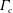$\unicode[STIX]{x1D6E4}_{c}$ represents, mathematically, the critical value of the parameter 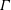$\unicode[STIX]{x1D6E4}$ below which a solution exists in the governing equations and, physically, the maximum angle of attack possible below which a laminar boundary layer will remain predominantly attached to the surface. Furthermore, we find that the dynamic roughness element impacts on the perturbation pressure gradient in two possible ways: either by decreasing the magnitude of the adverse pressure peak or by increasing the streamwise extent in which favourable pressure perturbations exist. Finally, we discover that the marginal separation bubble does not necessarily have to exist at 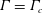$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{c}$ in the time-averaged flow and that full breakaway separation can therefore occur as a result of the bursting of transient bubbles existing within the length scale of marginal separation theory.

JFM classification

Boundary Layers: Boundary layer control Boundary Layers: Boundary layer separation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 351 - 370
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Braun, S. & Kluwick, A. 2002 The effect of three-dimensional obstacles on marginally separated laminar boundary layer flows. J. Fluid Mech. 460, 57–82.Google Scholar
Braun, S. & Kluwick, A. 2004 Unsteady three-dimensional marginal separation caused by surface-mounted obstacles and/or local suction. J. Fluid Mech. 514, 121–152.Google Scholar
Braun, S. & Scheichl, S. 2014 On recent developments in marginal separation theory. Phil. Trans. R. Soc. Lond. A 372 (2020), 20130343.Google Scholar
Cheng, H. K. & Smith, F. T. 1982 The influence of airfoil thickness and Reynolds number on separation. Z. Angew. Math. Phys. 33 (2), 151–180.Google Scholar
Dearing, S. S., Morrison, J. F. & Iannucci, L. 2010 Electro-active polymer (EAP) ‘dimple’ actuators for flow control: design and characterisation. Sensors Actuators A 157, 210–218.Google Scholar
Gad-el-Hak, M. 2000 Flow Control: Passive, Active and Reactive Flow Management. Cambridge University Press.Google Scholar
Goldstein, S. 1948 On laminar boundary-layer flow near a position of separation. Q. J. Mech. Appl. Maths 1 (1), 43–69.Google Scholar
Gouder, K., Potter, M. & Morrison, J. F. 2013 Turbulent friction drag reduction using electroactive polymer and electromagnetically driven surfaces. Exp. Fluids 54 (1), 1441.Google Scholar
Grager, T., Rothmayer, A. P., Huebsch, W. W. & Hu, H. 2012 Low Reynolds number stall suppression with dynamic roughness. In 6th AIAA Flow Control Conference, pp. 25–28. American Institute of Aeronautics and Astronautics.Google Scholar
Hsiao, C.-T. & Pauley, L. L. 1994 Comparison of the triple-deck theory, interactive boundary layer method, and Navier–Stokes computation for marginal separation. J. Fluids Engng 116, 22–28.Google Scholar
Huebsch, W. W. 2006 Two-dimensional simulation of dynamic surface roughness for aerodynamic flow control. J. Aircraft 43 (2), 353–362.Google Scholar
Huebsch, W. W., Gall, P. D., Hamburg, S. D. & Rothmayer, A. P. 2012 Dynamic roughness as a means of leading-edge separation flow control. J. Aircraft 49 (1), 108–115.Google Scholar
Huebsch, W. W. & Rothmayer, A. P. 2002 Effects of surface ice roughness on dynamic stall. J. Aircraft 39 (6), 945–953.Google Scholar
Kluwick, A., Braun, S. & Cox, E. A. 2008 Near critical phenomena in laminar boundary layers. J. Fluids Struct. 24 (8), 1185–1193.Google Scholar
Lissaman, P. B. S. 1983 Low-Reynolds-number airfoils. Annu. Rev. Fluid Mech. 15 (1), 223–239.Google Scholar
Rothmayer, A. P. & Huebsch, W. W. 2011 On the modification of laminar boundary layers using unsteady surface actuation. In 6th AIAA Theoretical Fluid Mechanics Conference, AIAA Paper 2011–4016, American Institute of Aeronautics and Astronautics.Google Scholar
Ruban, A. I. 1981 Singular solution of boundary layer equations which can be extended continuously through the point of zero surface friction. Fluid Dyn. 16 (6), 835–843.Google Scholar
Ruban, A. I. 1982 Asymptotic theory of short separation regions on the leading edge of a slender airfoil. Fluid Dyn. 17 (1), 33–41.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary Layer Theory. Springer.Google Scholar
Servini, P., Smith, F. T. & Rothmayer, A. P. 2017 The impact of static and dynamic roughness elements on flow separation. J. Fluid Mech. 830, 35–62.Google Scholar
Smith, F. T. 1982 Concerning dynamic stall. Aeronaut. Q. 33, 331–352.Google Scholar
Smith, F. T. & Daniels, P. G. 1981 Removal of Goldstein’s singularity at separation, in flow past obstacles in wall layers. J. Fluid Mech. 110, 1–37.Google Scholar
Stewartson, K. 1970 Is the singularity at separation removable? J. Fluid Mech. 44 (2), 347–364.Google Scholar
Stewartson, K., Smith, F. T. & Kaups, K. 1982 Marginal separation. Stud. Appl. Maths 67, 45–61.Google Scholar
Sychev, V. V., Ruban, A. I., Sychev, V. V. & Korolev, G. L. 1998 Asymptotic Theory of Separated Flows. Cambridge University Press.Google Scholar
Timoshin, S. N. 1988 Elimination of edge rupture caused by the effect of flow pulsations. J. Appl. Math. Mech. 52 (1), 59–62.Google Scholar
Zametaev, V. B. 1986 Existence and nonuniqueness of local separation zones in viscous jets. Fluid Dyn. 21 (1), 31–38.Google Scholar