Article contents
Hydrodynamic interactions between aerosol particles in the transition regime
Published online by Cambridge University Press: 19 September 2018
Abstract
We present a method for calculating the hydrodynamic interactions between particles in the kinetic (or transition regime), characterized by non-negligible particle Knudsen numbers. Such particles are often present in aerosol systems. The method is based on our extended Kirkwood–Riseman theory (Corson et al., Phys. Rev. E, vol. 95 (1), 2017c, 013103), which accounts for interactions between spheres using the velocity field around a translating sphere as a function of Knudsen number. Results for the two-sphere problem at small Knudsen numbers are in good agreement with those obtained using Felderhof’s interaction actions for mixed slip-stick boundary conditions, which are accurate to order 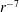 $r^{-7}$ (Felderhof, Physica A, vol. 89 (2), 1977, pp. 373–384). The strength of the interactions decreases with increasing Knudsen number. Results for two fractal aggregates demonstrate that one can apply a point force approach for interactions between particles in the transition regime; the interaction tensor is similar to the Oseen tensor for continuum flow. Using this point force approach, we present an analysis for the settling of an unbounded cloud of particles. Our analysis shows that for sufficiently high volume fractions and cloud radii, the cloud behaves as a gas droplet in continuum flow even when the individual particles are small relative to the mean free path of the gas. The method presented here can be applied in a Brownian dynamics simulation analogous to Stokesian dynamics to study the behaviour of a dense aerosol system.
$r^{-7}$ (Felderhof, Physica A, vol. 89 (2), 1977, pp. 373–384). The strength of the interactions decreases with increasing Knudsen number. Results for two fractal aggregates demonstrate that one can apply a point force approach for interactions between particles in the transition regime; the interaction tensor is similar to the Oseen tensor for continuum flow. Using this point force approach, we present an analysis for the settling of an unbounded cloud of particles. Our analysis shows that for sufficiently high volume fractions and cloud radii, the cloud behaves as a gas droplet in continuum flow even when the individual particles are small relative to the mean free path of the gas. The method presented here can be applied in a Brownian dynamics simulation analogous to Stokesian dynamics to study the behaviour of a dense aerosol system.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 5
- Cited by



