Hostname: page-component-6587cd75c8-cpvbf Total loading time: 0 Render date: 2025-04-24T06:43:46.192Z Has data issue: false hasContentIssue false
  • English
  • Français

How interfacial tension enhances drag in turbulent Taylor–Couette flow with neutrally buoyant and equally viscous droplets

Published online by Cambridge University Press:  23 December 2024

Jinghong Su Open the ORCID record for Jinghong Su [Opens in a new window] ,
Yi-Bao Zhang Open the ORCID record for Yi-Bao Zhang [Opens in a new window] ,
Cheng Wang Open the ORCID record for Cheng Wang [Opens in a new window] ,
Lei Yi Open the ORCID record for Lei Yi [Opens in a new window] ,
Fan Xu Open the ORCID record for Fan Xu [Opens in a new window] ,
Yaning Fan Open the ORCID record for Yaning Fan [Opens in a new window] ,
Junwu Wang Open the ORCID record for Junwu Wang [Opens in a new window]  and
Chao Sun Open the ORCID record for Chao Sun [Opens in a new window]
Jinghong Su
Affiliation:
New Cornerstone Science Laboratory, Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, 100084 Beijing, PR China
Yi-Bao Zhang
Affiliation:
New Cornerstone Science Laboratory, Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, 100084 Beijing, PR China
Cheng Wang
Affiliation:
New Cornerstone Science Laboratory, Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, 100084 Beijing, PR China
Lei Yi
Affiliation:
New Cornerstone Science Laboratory, Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, 100084 Beijing, PR China
Fan Xu
Affiliation:
State Key Laboratory of Mesoscience and Engineering, Institute of Process Engineering, Chinese Academy of Sciences, P. O. Box 353, Beijing 100190, PR China
Yaning Fan
Affiliation:
New Cornerstone Science Laboratory, Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, 100084 Beijing, PR China
Junwu Wang*
Affiliation:
State Key Laboratory of Mesoscience and Engineering, Institute of Process Engineering, Chinese Academy of Sciences, P. O. Box 353, Beijing 100190, PR China Beijing Key Laboratory of Process Fluid Filtration and Separation, College of Mechanical and Transportation Engineering, China University of Petroleum, Beijing 102249, PR China
Chao Sun*
Affiliation:
New Cornerstone Science Laboratory, Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, 100084 Beijing, PR China Department of Engineering Mechanics, School of Aerospace Engineering, Tsinghua University, Beijing 100084, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

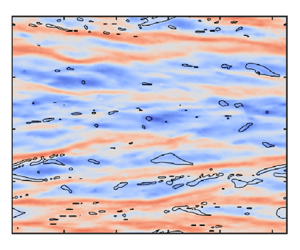
The presence of dispersed-phase droplets can result in a notable increase in a system's drag. However, our understanding of the mechanism underlying this phenomenon remains limited. In this study, we use three-dimensional direct numerical simulations with a modified multi-marker volume-of-fluid method to investigate liquid–liquid two-phase turbulence in a Taylor–Couette geometry. The dispersed phase has the same density and viscosity as the continuous phase. The Reynolds number $Re\equiv r_i\omega _i d/\nu$ is fixed at 5200, the volume fraction of the dispersed phase is up to $40\,\%$, and the Weber number $We\equiv \rho u^2_\tau d/\sigma$ is approximately 8. It is found that the increase in the system's drag originates from the contribution of interfacial tension. Specifically, droplets experience significant deformation and stretching in the streamwise direction due to shear near the inner cylinder. Consequently, the rear end of the droplets lags behind the fore head. This causes opposing interfacial tension effects on the fore head and rear end of the droplets. For the fore head of the droplets, the effect of interfacial tension appears to act against the flow direction. For the rear end, the effect appears to act in the flow direction. The increase in the system's drag is attributed primarily to the effect of interfacial tension on the fore head of the droplets which leads to the hindering effect of the droplets on the surrounding continuous phase. This hindering effect disrupts the formation of high-speed streaks, favouring the formation of low-speed ones, which are generally associated with higher viscous stress and drag of the system. This study provides new insights into the mechanism of drag enhancement reported in our previous experiments.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1002 , 10 January 2025 , A2
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

‡

J.S. and Y.-B.Z. contributed equally to this work.

References

Ardekani, M.N. & Brandt, L. 2019 Turbulence modulation in channel flow of finite-size spheroidal particles. J. Fluid Mech. 859, 887–901.CrossRefGoogle Scholar
Assen, M.P.A., Ng, C.S., Will, J.B., Stevens, R.J.A.M., Lohse, D. & Verzicco, R. 2022 Strong alignment of prolate ellipsoids in Taylor–Couette flow. J. Fluid Mech. 935, A7.CrossRefGoogle Scholar
Bakhuis, D., Ezeta, R., Bullee, P.A., Marin, A., Lohse, D., Sun, C. & Huisman, S.G. 2021 Catastrophic phase inversion in high-Reynolds-number turbulent Taylor–Couette flow. Phys. Rev. Lett. 126 (6), 064501.CrossRefGoogle ScholarPubMed
Balcázar, N., Lehmkuhl, O., Rigola, J. & Oliva, A. 2015 A multiple marker level-set method for simulation of deformable fluid particles. Intl J. Multiphase Flow 74, 125–142.CrossRefGoogle Scholar
Barcilon, A., Brindley, J., Lessen, M. & Mobbs, F.R. 1979 Marginal instability in Taylor–Couette flows at a very high Taylor number. J. Fluid Mech. 94 (3), 453–463.CrossRefGoogle Scholar
Brauckmann, H.J. & Eckhardt, B. 2013 Direct numerical simulations of local and global torque in Taylor–Couette flow up to $Re= 30\,000$. J. Fluid Mech. 718, 398–427.CrossRefGoogle Scholar
Chen, S., Zhao, W. & Wan, D. 2022 Turbulent structures and characteristics of flows past a vertical surface-piercing finite circular cylinder. Phys. Fluids 34 (1), 015115.CrossRefGoogle Scholar
Coyajee, E. & Boersma, B.J. 2009 Numerical simulation of drop impact on a liquid–liquid interface with a multiple marker front-capturing method. J. Comput. Phys. 228 (12), 4444–4467.CrossRefGoogle Scholar
Crialesi-Esposito, M., Rosti, M.E., Chibbaro, S. & Brandt, L. 2022 Modulation of homogeneous and isotropic turbulence in emulsions. J. Fluid Mech. 940, A19.CrossRefGoogle Scholar
Dodd, M.S. & Ferrante, A. 2016 On the interaction of Taylor length scale size droplets and isotropic turbulence. J. Fluid Mech. 806, 356–412.CrossRefGoogle Scholar
Dong, S. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 587, 373–393.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.CrossRefGoogle Scholar
Elghobashi, S. 2019 Direct numerical simulation of turbulent flows laden with droplets or bubbles. Annu. Rev. Fluid Mech. 51, 217–244.CrossRefGoogle Scholar
Girotto, I., Scagliarini, A., Benzi, R. & Toschi, F. 2024 Lagrangian statistics of concentrated emulsions. J. Fluid Mech. 986, A33.CrossRefGoogle Scholar
Hasslberger, J., Cifani, P., Chakraborty, N. & Klein, M. 2020 A direct numerical simulation analysis of coherent structures in bubble-laden channel flows. J. Fluid Mech. 905, A37.CrossRefGoogle Scholar
Holzmann, T. 2016 Mathematics, Numerics, Derivations and OpenFOAM $\circledR$. Holzmann CFD.Google Scholar
Hori, N., Ng, C.S., Lohse, D. & Verzicco, R. 2023 Interfacial-dominated torque response in liquid–liquid Taylor–Couette flows. J. Fluid Mech. 956, A15.CrossRefGoogle Scholar
Huisman, S.G., Scharnowski, S., Cierpka, C., Kähler, C.J., Lohse, D. & Sun, C. 2013 Logarithmic boundary layers in strong Taylor–Couette turbulence. Phys. Rev. Lett. 110 (26), 264501.CrossRefGoogle ScholarPubMed
Innocenti, A., Jaccod, A., Popinet, S. & Chibbaro, S. 2021 Direct numerical simulation of bubble-induced turbulence. J. Fluid Mech. 918, A23.CrossRefGoogle Scholar
Kilpatrick, P.K. 2012 Water-in-crude oil emulsion stabilization: review and unanswered questions. Energy Fuels 26 (7), 4017–4026.CrossRefGoogle Scholar
Krieger, I.M. & Dougherty, T.J. 1959 A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 3 (1), 137–152.CrossRefGoogle Scholar
Mangani, F., Roccon, A., Zonta, F. & Soldati, A. 2024 Heat transfer in drop-laden turbulence. J. Fluid Mech. 978, A12.CrossRefGoogle Scholar
Mathai, V., Lohse, D. & Sun, C. 2020 Bubbly and buoyant particle-laden turbulent flows. Annu. Rev. Condens. Matter Phys. 11, 529–559.CrossRefGoogle Scholar
Maxey, M.R. 2017 Droplets in turbulence: a new perspective. J. Fluid Mech. 816, 1–4.CrossRefGoogle Scholar
McClements, D.J. 2007 Critical review of techniques and methodologies for characterization of emulsion stability. Crit. Rev. Food Sci. 47 (7), 611–649.CrossRefGoogle ScholarPubMed
Mukherjee, S., Safdari, A., Shardt, O., Kenjereš, S. & Van den Akker, H.E.A. 2019 Droplet–turbulence interactions and quasi-equilibrium dynamics in turbulent emulsions. J. Fluid Mech. 878, 221–276.CrossRefGoogle Scholar
Nemati, H., Breugem, W.-P., Kwakkel, M. & Boersma, B.J. 2021 Direct numerical simulation of turbulent bubbly down flow using an efficient CLSVOF method. Intl J. Multiphase Flow 135, 103500.CrossRefGoogle Scholar
Ni, R. 2024 Deformation and breakup of bubbles and drops in turbulence. Annu. Rev. Fluid Mech. 56, 319–347.CrossRefGoogle Scholar
Ostilla, R., Stevens, R.J.A.M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.CrossRefGoogle Scholar
Picano, F., Breugem, W.-P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.CrossRefGoogle Scholar
Popinet, S. 2018 Numerical models of surface tension. Annu. Rev. Fluid Mech. 50 (1), 49–75.CrossRefGoogle Scholar
Rosti, M.E., Brandt, L. & Mitra, D. 2018 Rheology of suspensions of viscoelastic spheres: deformability as an effective volume fraction. Phys. Rev. Fluids 3 (1), 012301.CrossRefGoogle Scholar
Rosti, M.E., Ge, Z., Jain, S.S., Dodd, M.S. & Brandt, L. 2019 Droplets in homogeneous shear turbulence. J. Fluid Mech. 876, 962–984.CrossRefGoogle Scholar
Rosti, M.E. & Takagi, S. 2021 Shear-thinning and shear-thickening emulsions in shear flows. Phys. Fluids 33 (8), 083319.CrossRefGoogle Scholar
Rusche, H. 2003 Computational fluid dynamics of dispersed two-phase flows at high phase fractions. PhD thesis, Imperial College London, University of London.Google Scholar
Scarbolo, L., Bianco, F. & Soldati, A. 2016 Turbulence modification by dispersion of large deformable droplets. Eur. J. Mech. (B/Fluids) 55, 294–299.CrossRefGoogle Scholar
Scarbolo, L. & Soldati, A. 2015 Wall drag modification by large deformable droplets in turbulent channel flow. Comput. Fluids 113, 87–92.CrossRefGoogle Scholar
Scheufler, H. & Roenby, J. 2019 Accurate and efficient surface reconstruction from volume fraction data on general meshes. J. Comput. Phys. 383, 1–23.CrossRefGoogle Scholar
Soligo, G., Roccon, A. & Soldati, A. 2019 Breakage, coalescence and size distribution of surfactant-laden droplets in turbulent flow. J. Fluid Mech. 881, 244–282.CrossRefGoogle Scholar
Soligo, G., Roccon, A. & Soldati, A. 2021 Turbulent flows with drops and bubbles: what numerical simulations can tell us – Freeman scholar lecture. Trans. ASME J. Fluids Engng 143 (8), 080801.CrossRefGoogle Scholar
Spandan, V., Verzicco, R. & Lohse, D. 2018 Physical mechanisms governing drag reduction in turbulent Taylor–Couette flow with finite-size deformable bubbles. J. Fluid Mech. 849, R3.CrossRefGoogle Scholar
Spernath, A. & Aserin, A. 2006 Microemulsions as carriers for drugs and nutraceuticals. Adv. Colloid Interface Sci. 128, 47–64.CrossRefGoogle ScholarPubMed
Su, J., Wang, C., Zhang, Y.-B., Xu, F., Wang, J. & Sun, C. 2024 a Turbulence modulation in liquid–liquid two-phase Taylor–Couette turbulence. J. Fluid Mech. 999, A98.CrossRefGoogle Scholar
Su, J., Yi, L., Zhao, B., Wang, C., Xu, F., Wang, J. & Sun, C. 2024 b Numerical study on the mechanism of drag modulation by dispersed drops in two-phase Taylor–Couette turbulence. J. Fluid Mech. 984, R3.CrossRefGoogle Scholar
Thomas, S., Esmaeeli, A. & Tryggvason, G. 2010 Multiscale computations of thin films in multiphase flows. Intl J. Multiphase Flow 36 (1), 71–77.CrossRefGoogle Scholar
de Vita, F., Rosti, M.E., Caserta, S. & Brandt, L. 2019 On the effect of coalescence on the rheology of emulsions. J. Fluid Mech. 880, 969–991.CrossRefGoogle Scholar
Wang, C., Jiang, L. & Sun, C. 2023 Numerical study on turbulence modulation of finite-size particles in plane-Couette flow. J. Fluid Mech. 970, A7.CrossRefGoogle Scholar
Wang, C., Yi, L., Jiang, L. & Sun, C. 2022 Turbulence drag modulation by dispersed droplets in Taylor–Couette flow: the effects of the dispersed phase viscosity. J. Fluid Mech. 952, A39.CrossRefGoogle Scholar
Wang, G., Abbas, M. & Climent, E. 2017 Modulation of large-scale structures by neutrally buoyant and inertial finite-size particles in turbulent Couette flow. Phys. Rev. Fluids 2 (8), 084302.CrossRefGoogle Scholar
Wang, L., Li, X., Zhang, G., Dong, J. & Eastoe, J. 2007 Oil-in-water nanoemulsions for pesticide formulations. J. Colloid Interface Sci. 314 (1), 230–235.CrossRefGoogle ScholarPubMed
Xu, F., Su, J., Lan, B., Zhao, P., He, Y., Sun, C. & Wang, J. 2023 Direct numerical simulation of Taylor–Couette flow with vertical asymmetric rough walls. J. Fluid Mech. 975, A30.CrossRefGoogle Scholar
Xu, F., Zhao, P., Sun, C., He, Y. & Wang, J. 2022 Direct numerical simulation of Taylor–Couette flow: regime-dependent role of axial walls. Chem. Engng Sci. 263, 118075.CrossRefGoogle Scholar
Yi, L., Toschi, F. & Sun, C. 2021 Global and local statistics in turbulent emulsions. J. Fluid Mech. 912, A13.CrossRefGoogle Scholar
Yi, L., Wang, C., Huisman, S.G. & Sun, C. 2023 Recent developments of turbulent emulsions in Taylor–Couette flow. Phil. Trans. R. Soc. Lond. A 381 (2243), 20220129.Google ScholarPubMed
Yi, L., Wang, C., van Vuren, T., Lohse, D., Risso, F., Toschi, F. & Sun, C. 2022 Physical mechanisms for droplet size and effective viscosity asymmetries in turbulent emulsions. J. Fluid Mech. 951, A39.CrossRefGoogle Scholar
Zhu, X., Ostilla-Mónico, R., Verzicco, R. & Lohse, D. 2016 Direct numerical simulation of Taylor–Couette flow with grooved walls: torque scaling and flow structure. J. Fluid Mech. 794, 746–774.CrossRefGoogle Scholar