Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T17:35:18.515Z Has data issue: false hasContentIssue false
  • English
  • Français

How do the finite-size particles modify the drag in Taylor–Couette turbulent flow

Published online by Cambridge University Press:  22 February 2022

Cheng Wang Open the ORCID record for Cheng Wang [Opens in a new window] ,
Lei Yi Open the ORCID record for Lei Yi [Opens in a new window] ,
Linfeng Jiang Open the ORCID record for Linfeng Jiang [Opens in a new window]  and
Chao Sun Open the ORCID record for Chao Sun [Opens in a new window]
Cheng Wang
Affiliation:
Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, PR China
Lei Yi
Affiliation:
Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, PR China
Linfeng Jiang
Affiliation:
Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, PR China
Chao Sun*
Affiliation:
Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, PR China Department of Engineering Mechanics, School of Aerospace Engineering, Tsinghua University, Beijing 100084, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

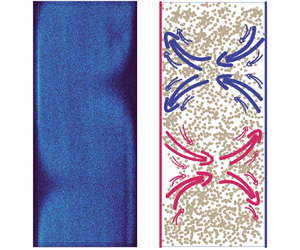
We experimentally investigate the drag modification by neutrally buoyant finite-size particles with various aspect ratios in a Taylor–Couette (TC) turbulent flow. The current Reynolds number, $Re$, ranges from $6.5\times 10^3$ to $2.6\times 10^4$, and the particle volume fraction, $\varPhi$, is up to $10\,\%$. Particles with three kinds of aspect ratio, $\lambda$, are used: $\lambda =1/3$ (oblate), $\lambda =1$ (spherical) and $\lambda =3$ (prolate). Unlike the case of bubbly TC flow (van Gils et al., J. Fluid Mech., vol. 722, 2013, pp. 317–347; Verschoof et al., Phys. Rev. Lett., vol. 117, issue 10, 2016, p. 104502), we find that the suspended finite-size particles increase the drag of the TC system regardless of their aspect ratios. The overall drag of the system increases with increasing $Re$, which is consistent with the literature. In addition, the normalized friction coefficient, $c_{f,\varPhi }/c_{f,\varPhi =0}$, decreases with increasing $Re$, the reason could be that in the current low volume fractions the turbulent stress becomes dominant at higher $Re$. The particle distributions along the radial direction of the system are obtained by performing optical measurements at $\varPhi =0.5\,\%$ and $\varPhi = 2\,\%$. As $Re$ increases, the particles distribute more evenly in the entire system, which results from both the greater turbulence intensity and the more pronounced finite-size effects of the particles at higher $Re$. Moreover, it is found that the variation of the particle aspect ratios leads to different particle collective effects. The suspended spherical particles, which tend to cluster near the walls and form a particle layer, significantly affect the boundary layer and result in maximum drag modification. The minimal drag modification is found in the oblate case, where the particles preferentially cluster in the bulk region, and, thus, the particle layer is absent. Based on the optical measurement results, it can be concluded that, in the low volume fraction ranges ($\varPhi =0.5\,\%$ and $\varPhi = 2\,\%$ here), the larger drag modification is connected to the near-wall particle clustering. The present findings suggest that the particle shape plays a significant role in drag modification, and the collective behaviours of rigid particles provide clues to understand the bubbly drag reduction.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 937 , 25 April 2022 , A15
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adams, S., Frith, W.J. & Stokes, J.R. 2004 Influence of particle modulus on the rheological properties of agar microgel suspensions. J. Rheol. 48 (6), 1195–1213.CrossRefGoogle Scholar
Alméras, E., Mathai, V., Lohse, D. & Sun, C. 2017 Experimental investigation of the turbulence induced by a bubble swarm rising within incident turbulence. J. Fluid Mech. 825, 1091–1112.CrossRefGoogle Scholar
Ardekani, M.N. & Brandt, L. 2019 Turbulence modulation in channel flow of finite-size spheroidal particles. J. Fluid Mech. 859, 887–901.CrossRefGoogle Scholar
Ardekani, M.N., Costa, P., Breugem, W.-P., Picano, F. & Brandt, L. 2017 Drag reduction in turbulent channel flow laden with finite-size oblate spheroids. J. Fluid Mech. 816, 43–70.CrossRefGoogle Scholar
Assen, M.P.A., Ng, C.S., Will, J.B., Stevens, R.J.A.M., Lohse, D. & Verzicco, R. 2022 Strong alignment of prolate ellipsoids in Taylor–Couette flow. J. Fluid Mech. 935, A7.CrossRefGoogle Scholar
Bagnold, R.A. 1954 Experiments on a gravity-free dispersion of large solid spheres in a newtonian fluid under shear. Proc. R. Soc. Lond. A 225 (1160), 49–63.Google Scholar
Bakhuis, D., Ezeta, R., Bullee, P.A., Marin, A., Lohse, D., Sun, C. & Huisman, S.G. 2021 Catastrophic phase inversion in high-Reynolds-number turbulent Taylor–Couette flow. Phys. Rev. Lett. 126 (6), 064501.CrossRefGoogle ScholarPubMed
Bakhuis, D., Verschoof, R.A., Mathai, V., Huisman, S.G., Lohse, D. & Sun, C. 2018 Finite-sized rigid spheres in turbulent Taylor–Couette flow: effect on the overall drag. J. Fluid Mech. 850, 246–261.CrossRefGoogle Scholar
Batchelor, G.K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41 (3), 545–570.CrossRefGoogle Scholar
van den Berg, T.H., van Gils, D.P.M., Lathrop, D.P. & Lohse, D. 2007 Bubbly turbulent drag reduction is a boundary layer effect. Phys. Rev. Lett. 98 (8), 084501.CrossRefGoogle ScholarPubMed
van den Berg, T.H., Luther, S., Lathrop, D.P. & Lohse, D. 2005 Drag reduction in bubbly Taylor–Couette turbulence. Phys. Rev. Lett. 94 (4), 044501.CrossRefGoogle ScholarPubMed
Calzavarini, E., Cencini, M., Lohse, D. & Toschi, F. 2008 Quantifying turbulence-induced segregation of inertial particles. Phys. Rev. Lett. 101 (8), 084504.CrossRefGoogle ScholarPubMed
Colin, C., Fabre, J. & Kamp, A. 2012 Turbulent bubbly flow in pipe under gravity and microgravity conditions. J. Fluid Mech. 711, 469–515.CrossRefGoogle Scholar
Costa, P., Picano, F., Brandt, L. & Breugem, W.-P. 2016 Universal scaling laws for dense particle suspensions in turbulent wall-bounded flows. Phys. Rev. Lett. 117, 134501.CrossRefGoogle ScholarPubMed
Cristancho, D.M., Delgado, D.R., Martinez, F., Abolghassemi Fakhree, M.A. & Jouyban, A. 2011 Volumetric properties of glycerol+ water mixtures at several temperatures and correlation with the Jouyban-Acree model. Rev. Colomb. Cienc. Quim. Farm. 40 (1), 92–115.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2000 Scaling of global momentum transport in Taylor–Couette and pipe flow. Eur. Phys. J. B 18 (3), 541–544.CrossRefGoogle Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52 (4), 309–329.CrossRefGoogle Scholar
Ezeta, R., Bakhuis, D., Huisman, S.G., Sun, C. & Lohse, D. 2019 Drag reduction in boiling Taylor–Couette turbulence. J. Fluid Mech. 881, 104–118.CrossRefGoogle Scholar
Fall, A., Lemaitre, A., Bertrand, F., Bonn, D. & Ovarlez, G. 2010 Shear thickening and migration in granular suspensions. Phys. Rev. Lett. 105 (26), 268303.CrossRefGoogle ScholarPubMed
Fornari, W., Formenti, A., Picano, F. & Brandt, L. 2016 The effect of particle density in turbulent channel flow laden with finite size particles in semi-dilute conditions. Phys. Fluids 28 (3), 033301.CrossRefGoogle Scholar
Frankel, A., Pouransari, H., Coletti, F. & Mani, A. 2016 Settling of heated particles in homogeneous turbulence. J. Fluid Mech. 792, 869–893.CrossRefGoogle Scholar
van Gils, D.P.M., Guzman, D.N., Sun, C. & Lohse, D. 2013 The importance of bubble deformability for strong drag reduction in bubbly turbulent Taylor–Couette flow. J. Fluid Mech. 722, 317–347.CrossRefGoogle Scholar
van Gils, D.P.M., Huisman, S.G., Bruggert, G.-W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counterrotating cylinders. Phys. Rev. Lett. 106 (2), 024502.CrossRefGoogle ScholarPubMed
Greidanus, A.J., Delfos, R. & Westerweel, J. 2011 Drag reduction by surface treatment in turbulent Taylor–Couette flow. J. Phys.: Conf. Ser. 318 (8), 082016.Google Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High-Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.CrossRefGoogle Scholar
Guazzelli, É. & Pouliquen, O. 2018 Rheology of dense granular suspensions. J. Fluid Mech. 852, P1.CrossRefGoogle Scholar
Herschel, W.H. & Bulkley, R. 1926 Konsistenzmessungen von gummi-benzollösungen. Kolloidn. Z. 39 (4), 291–300.CrossRefGoogle Scholar
Hu, H., et al. 2017 Significant and stable drag reduction with air rings confined by alternated superhydrophobic and hydrophilic strips. Sci. Adv. 3 (9), e1603288.CrossRefGoogle ScholarPubMed
Huisman, S.G., Van Der Veen, R.C., Sun, C. & Lohse, D. 2014 Multiple states in highly turbulent Taylor–Couette flow. Nat. Commun. 5 (1), 3820.CrossRefGoogle ScholarPubMed
Hunt, M.L., Zenit, R., Campbell, C.S. & Brennen, C.E. 2002 Revisiting the 1954 suspension experiments of R. A. Bagnold. J. Fluid Mech. 452, 1–24.CrossRefGoogle Scholar
Jiang, L., Calzavarini, E. & Sun, C. 2020 Rotation of anisotropic particles in Rayleigh–Bénard turbulence. J. Fluid Mech. 901, A8.CrossRefGoogle Scholar
Krieger, I.M. & Dougherty, T.J. 1959 A mechanism for non-newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 3 (1), 137–152.CrossRefGoogle Scholar
Lashgari, I., Picano, F., Breugem, W.-P. & Brandt, L. 2014 Laminar, turbulent, and inertial shear-thickening regimes in channel flow of neutrally buoyant particle suspensions. Phys. Rev. Lett. 113 (25), 254502.CrossRefGoogle ScholarPubMed
Lathrop, D.P., Fineberg, J. & Swinney, H.L. 1992 Transition to shear-driven turbulence in Couette-Taylor flow. Phys. Rev. A 46 (10), 6390.CrossRefGoogle ScholarPubMed
Lohse, D. 2018 Bubble puzzles: from fundamentals to applications. Phys. Rev. Fluids 3 (11), 110504.CrossRefGoogle Scholar
Lovecchio, S., Climent, E., Stocker, R. & Durham, W.M. 2019 Chain formation can enhance the vertical migration of phytoplankton through turbulence. Sci. Adv. 5 (10), eaaw7879.CrossRefGoogle Scholar
Lu, C., Xia, S., Shao, M. & Fu, Y. 2020 Arc-support line segments revisited: an efficient high-quality ellipse detection. IEEE Trans. Image Process. 29, 768–781.CrossRefGoogle Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32 (1), 659–708.CrossRefGoogle Scholar
Maryami, R., Farahat, S., Javad Poor, M. & Mayam, M.H.S. 2014 Bubbly drag reduction in a vertical Couette-Taylor system with superimposed axial flow. Fluid Dyn. Res. 46 (5), 055504.CrossRefGoogle Scholar
Mathai, V., Huisman, S.G., Sun, C., Lohse, D. & Bourgoin, M. 2018 Dispersion of air bubbles in isotropic turbulence. Phys. Rev. Lett. 121 (5), 054501.CrossRefGoogle ScholarPubMed
Mathai, V., Lohse, D. & Sun, C. 2020 Bubbly and buoyant particle-laden turbulent flows. Annu. Rev. Condens. Matter Phys. 11, 529–559.CrossRefGoogle Scholar
Mittal, R., Ni, R. & Seo, J.-H. 2020 The flow physics of Covid-19. J. Fluid Mech. 894, F2.CrossRefGoogle Scholar
Olivucci, P., Wise, D.J. & Ricco, P. 2021 Reduction of turbulent skin-friction drag by passively rotating discs. J. Fluid Mech. 923, A8.CrossRefGoogle Scholar
Park, H.J., O'Keefe, K. & Richter, D.H. 2018 Rayleigh-Bénard turbulence modified by two-way coupled inertial, nonisothermal particles. Phys. Rev. Fluids 3 (3), 034307.CrossRefGoogle Scholar
Pedley, T.J. & Kessler, J.O. 1992 Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24 (1), 313–358.CrossRefGoogle Scholar
Peskin, C.S. 2002 The immersed boundary method. Acta Numer. 11, 479–517.CrossRefGoogle Scholar
Picano, F., Breugem, W.-P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.CrossRefGoogle Scholar
Picano, F., Breugem, W.-P., Mitra, D. & Brandt, L. 2013 Shear thickening in non-brownian suspensions: an excluded volume effect. Phys. Rev. Lett. 111 (9), 098302.CrossRefGoogle Scholar
Rosti, M.E. & Takagi, S. 2021 Shear-thinning and shear-thickening emulsions in shear flows. Phys. Fluids 33 (8), 083319.CrossRefGoogle Scholar
Rusconi, R., Guasto, J.S. & Stocker, R. 2014 Bacterial transport suppressed by fluid shear. Nat. Phys. 10 (3), 212–217.CrossRefGoogle Scholar
Sanders, W.C., Winkel, E.S., Dowling, D.R., Perlin, M. & Ceccio, S.L. 2006 Bubble friction drag reduction in a high-Reynolds-number flat-plate turbulent boundary layer. J. Fluid Mech. 552, 353–380.CrossRefGoogle Scholar
Saw, E.W., Shaw, R.A., Ayyalasomayajula, S., Chuang, P.Y. & Gylfason, A. 2008 Inertial clustering of particles in high-Reynolds-number turbulence. Phys. Rev. Lett. 100 (21), 214501.CrossRefGoogle ScholarPubMed
Stickel, J.J. & Powell, R.L. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149.CrossRefGoogle Scholar
Tagawa, Y., Roghair, I., Prakash, V.N., van Sint Annaland, M., Kuipers, H., Sun, C. & Lohse, D. 2013 The clustering morphology of freely rising deformable bubbles. J. Fluid Mech. 721, A2.CrossRefGoogle Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.CrossRefGoogle Scholar
Uhlmann, M. 2008 Interface-resolved direct numerical simulation of vertical particulate channel flow in the turbulent regime. Phys. Fluids 20 (5), 053305.CrossRefGoogle Scholar
Verschoof, R.A., Van Der Veen, R.C.A., Sun, C. & Lohse, D. 2016 Bubble drag reduction requires large bubbles. Phys. Rev. Lett. 117 (10), 104502.CrossRefGoogle ScholarPubMed
Voth, G.A. & Soldati, A. 2017 Anisotropic particles in turbulence. Annu. Rev. Fluid Mech. 49, 249–276.CrossRefGoogle Scholar
Wang, G., Abbas, M. & Climent, É. 2017 a Modulation of large-scale structures by neutrally buoyant and inertial finite-size particles in turbulent couette flow. Phys. Rev. Fluids 2 (8), 084302.CrossRefGoogle Scholar
Wang, Y., Sierakowski, A.J. & Prosperetti, A. 2017 b Fully-resolved simulation of particulate flows with particles-fluid heat transfer. J. Comput. Phys. 350, 638–656.CrossRefGoogle Scholar
Wang, Z., Mathai, V. & Sun, C. 2019 Self-sustained biphasic catalytic particle turbulence. Nat. Commun. 10 (1), 3333.CrossRefGoogle ScholarPubMed
Wang, Z., Mathai, V. & Sun, C. 2020 Experimental study of the heat transfer properties of self-sustained biphasic thermally driven turbulence. Intl J. Heat Mass Transfer 152, 119515.CrossRefGoogle Scholar
Will, J.B., Mathai, V., Huisman, S.G., Lohse, D., Sun, C. & Krug, D. 2021 Kinematics and dynamics of freely rising spheroids at high-Reynolds-numbers. J. Fluid Mech. 912, A16.CrossRefGoogle Scholar
Yi, L., Toschi, F. & Sun, C. 2021 Global and local statistics in turbulent emulsions. J. Fluid Mech. 912, A13.CrossRefGoogle Scholar
Zade, S., Costa, P., Fornari, W., Lundell, F. & Brandt, L. 2018 Experimental investigation of turbulent suspensions of spherical particles in a square duct. J. Fluid Mech. 857, 748–783.CrossRefGoogle Scholar
Zhang, Q. & Prosperetti, A. 2010 Physics-based analysis of the hydrodynamic stress in a fluid-particle system. Phys. Fluids 22 (3), 033306.CrossRefGoogle Scholar