Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T06:49:46.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Homogeneous swarm of high-Reynolds-number bubbles rising within a thin gap. Part 2. Liquid dynamics

Published online by Cambridge University Press:  09 October 2014

Emmanuella Bouche ,
Véronique Roig ,
Frédéric Risso  and
Anne-Marie Billet
Emmanuella Bouche
Affiliation:
Institut de Mécanique des Fluides de Toulouse, Université de Toulouse (INPT, UPS) and CNRS, Allée C. Soula, 31400 Toulouse, France Fédération de Recherche FERMaT, CNRS, Allée C. Soula, 31400 Toulouse, France
Véronique Roig*
Affiliation:
Institut de Mécanique des Fluides de Toulouse, Université de Toulouse (INPT, UPS) and CNRS, Allée C. Soula, 31400 Toulouse, France Fédération de Recherche FERMaT, CNRS, Allée C. Soula, 31400 Toulouse, France
Frédéric Risso*
Affiliation:
Institut de Mécanique des Fluides de Toulouse, Université de Toulouse (INPT, UPS) and CNRS, Allée C. Soula, 31400 Toulouse, France Fédération de Recherche FERMaT, CNRS, Allée C. Soula, 31400 Toulouse, France
Anne-Marie Billet
Affiliation:
Laboratoire de Génie Chimique, Université de Toulouse (INPT, UPS) and CNRS, 4 Allée E. Monso, BP 74233, 31432 Toulouse CEDEX 4, France Fédération de Recherche FERMaT, CNRS, Allée C. Soula, 31400 Toulouse, France
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The agitation of the liquid phase has been investigated experimentally in a homogeneous swarm of bubbles rising at high Reynolds number within a thin gap. Owing to the wall friction, the bubble wakes are strongly attenuated. Consequently, liquid fluctuations result from disturbances localized near the bubbles and direct interactions between them. The signature of the average wake rapidly fades and the probability density function of the fluctuations becomes Gaussian as the gas volume fraction $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\alpha $ increases. The energy of the fluctuations scales differently with $\alpha $ depending on the direction, indicating that hydrodynamic interactions are different in the horizontal and vertical directions. 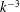The spatial spectrum shows that the length scales of the fluctuations are independent of $\alpha $ and exhibits a $k^{-3}$ subrange, which results from localized random flow disturbances of various sizes. Comparisons with the dynamics of the gas phase show that liquid and bubble agitations are driven by the same mechanism in the vertical direction, whereas they turn out to be almost uncoupled in the horizontal direction. Comparisons with unconfined flows show that the generation of liquid fluctuations is very different. However, the cause of the 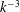$k^{-3}$ spectral subrange is the same for confined flows as for the spatial fluctuation of unconfined flows.

JFM classification

Drops and Bubbles: Drops and Bubbles Multiphase and Particle-laden Flows: Gas/liquid flow Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , pp. 508 - 521
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: CNRS, UMR 6614 CORIA, Université et INSA de Rouen, Avenue de l’Université, 76801 Saint Etienne du Rouvray, France.

References

Adrian, R. J. 1991 Particle imaging techniques for experimental fluid mechanics. Annu. Rev. Fluid Mech. 23, 261–304.Google Scholar
Bouche, E., Cazin, S., Roig, V. & Risso, F. 2013 Mixing in a swarm of bubbles rising in a confined cell measured by mean of PLIF with two different dyes. Exp. Fluids 54, 1552.Google Scholar
Bouche, E., Roig, V., Risso, F. & Billet, A. M. 2012 Homogeneous swarm of high-Reynolds-number bubbles rising within a thin gap. Part 1. Bubble dynamics. J. Fluid Mech. 704, 211–231.Google Scholar
Lance, M. & Bataille, J. 1991 Turbulence in the liquid phase of a uniform bubbly air–water flow. J. Fluid Mech. 222, 95–118.Google Scholar
Martinez Mercado, J., Chehata Gomez, D., van Gils, D., Sun, C. & Lohse, D. 2010 On bubble clustering and energy spectra in pseudo-turbulence. J. Fluid Mech. 650, 287–306.Google Scholar
Mendez-Diaz, S., Serrano-García, J. C. & Zenit, R. 2013 Power spectral distributions of pseudo-turbulent bubbly flows. Phys. Fluids 25, 043303.Google Scholar
Resen, J., Luther, S. & Lohse, D. 2005 The effect of bubbles on developed turbulence. J. Fluid Mech. 538, 153–187.Google Scholar
Riboux, G., Legendre, D. & Risso, F. 2013 A model of bubble-induced turbulence based on large-scale wake interactions. J. Fluid Mech. 719, 362–387.Google Scholar
Riboux, G., Risso, F. & Legendre, D. 2010 Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J. Fluid Mech. 643, 509–559.Google Scholar
Risso, F. 2011 Theoretical model for $k^{-3}$ spectra in dispersed multiphase flows. Phys. Fluids 23, 011701.Google Scholar
Risso, F. & Ellingsen, K. 2002 Velocity fluctuations in a homogeneous dilute dispersion of high-Reynolds-number rising bubbles. J. Fluid Mech. 453, 395–410.Google Scholar
Risso, F., Roig, V., Amoura, Z. & Billet, A.-M.2010 The dual nature of pseudo-turbulence analyzed from spatial and time averagings of a flow through random obstacles. In Proceedings of the 7th International Conference on Multiphase Flows (ICMF) 2010, Tampa, FL, 30 May–4 June.Google Scholar
Risso, F., Roig, V., Amoura, Z., Riboux, G. & Billet, A.-M. 2008 Wake attenuation in large Reynolds number dispersed two-phase flows. Phil. Trans. R. Soc. Lond. A 366, 2177–2190.Google Scholar
Roig, V. & Larue de Tournemine, A. 2007 Measurement of interstitial velocity of homogeneous bubble flows at low to moderate void fraction. J. Fluid Mech. 572, 87–110.Google Scholar
Roig, V., Roudet, M., Risso, F. & Billet, A.-M. 2011 Dynamics of a high-Reynolds-number bubble rising within a thin gap. J. Fluid Mech. 707, 444–466.Google Scholar
Roudet, M., Billet, A.-M., Risso, F. & Roig, V. 2011 PIV with volume lighting in a narrow cell: an efficient method to measure large velocity fields of rapidly varying flows. Exp. Therm. Fluid Sci. 35, 1030–1037.Google Scholar
Spicka, P., Dias, M. M. & Lopes, J. C. B. 2001 Gas–liquid flow in a 2D column: comparison between experimental data and CFD modelling. Chem. Engng Sci. 56, 6367–6383.Google Scholar
Tsao, H.-K. & Koch, D. L. 1994 Collisions of slightly deformable, high Reynolds number bubbles with short-range repulsive forces. Phys. Fluids 6, 2591–2625.Google Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39, 1096–1100.Google Scholar