Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T18:48:26.610Z Has data issue: false hasContentIssue false
  • English
  • Français

High spatial and temporal resolution study of shock wave reflection over a coupled convex–concave cylindrical surface

Published online by Cambridge University Press:  04 March 2015

O. Ram ,
M. Geva  and
O. Sadot
O. Ram
Affiliation:
Pearlstone Center for Aeronautical Engineering Studies, Department of Mechanical Engineering, Faculty of Engineering Sciences, Ben-Gurion University of the Negev, Beer Sheva, 8410501, Israel
M. Geva
Affiliation:
Pearlstone Center for Aeronautical Engineering Studies, Department of Mechanical Engineering, Faculty of Engineering Sciences, Ben-Gurion University of the Negev, Beer Sheva, 8410501, Israel
O. Sadot*
Affiliation:
Pearlstone Center for Aeronautical Engineering Studies, Department of Mechanical Engineering, Faculty of Engineering Sciences, Ben-Gurion University of the Negev, Beer Sheva, 8410501, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Studying the nature of transient reflections of shock waves from surfaces is important in many engineering fields, e.g. blast protection, supersonic flights, shock focusing, medical and industrial applications and more. The recent advancements in this field reveal that the major obstacle in better understanding this phenomenon by means of experimental investigations is the limited temporal and spatial resolution. An alternative approach to commonly used high-speed photography is based on the use of a single-lens reflex (SLR) camera that captures only one image per experiment. Using this method to study a transient reflection process necessitates repeating each experiment many times while retaining extremely high repeatability. In the present study, we present a solution to this obstacle by means of a fully automated shock tube facility, which has been developed in the course of this study. A typical experiment can be executed a few hundred times with a repeatability of less than 0.01 in the incident-shock-wave Mach number at moderate shock strengths (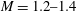$M=1.2{-}1.4$). The system offers a very high spatial and temporal resolution description of the transient reflection process of a shock wave over a coupled convex–concave surface. The study of this complex configuration using a fully automated shock tube enables one to observe, in greater detail than ever before, both the transient transition from regular reflection, RR, to Mach reflection, MR, and the reverse transient transition from MR to RR. The geometry studied can also be found in blunt leading-edge reflectors in which higher pressures were recorded, and the results presented also describe in detail the shock reflection process inside such a reflector. The results highlight and strengthen the recent understanding of the importance of high spatial and temporal resolution in determining the transition process from RR to MR over a coupled concave–convex surface. However, despite achieving very high statistical certainty in the experimental measurements, the question of the difference between the pseudo-steady transition criterion and the experimental results remains unresolved.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 768 , 10 April 2015 , pp. 219 - 239
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Equally contributed authors.

References

Babinsky, H., Onodera, O., Takayama, K., Saito, T., Voinovich, P. & Timofeev, E. 1998 The influence of entrance geometry of circular reflectors on the shock wave focusing. Comput. Fluids 27 (5–6), 611–618.CrossRefGoogle Scholar
Babinsky, H., Onodera, O., Takayama, K., Timofeev, E. & Voinovich, P. 1995 The influence of geometric variations on shock focusing in cylindrical cavities. In Proceedings of the 20th International Symposium on Shock Waves, Pasadena, California, USA, pp. 495–500. World Scientific Publishing Company Inc.Google Scholar
Ben-Dor, G. 2007 Shock Wave Reflection Phenomena. Springer.Google Scholar
Ben-Dor, G., Dewey, J. M., Mcmillian, D. J. & Takayama, K. 1988 Experimental investigation of the asymptotically approached Mach reflection over the second surface in a double wedge reflection. Exp. Fluids 6, 429–434.CrossRefGoogle Scholar
Ben-Dor, G., Dewey, J. M. & Takayama, K. 1987 The reflection of a plane shock wave over a double wedge. J. Fluid Mech. 176, 483–520.CrossRefGoogle Scholar
Ben-Dor, G. & Takayama, K. 1981 Streak camera photography with curved slits for the precise determination of shock wave transition phenomena. Can. Aeronaut. Space J. 27, 128–134.Google Scholar
Ben-Dor, G. & Takayama, K. 1986/1987 The dynamics of the transition from Mach to regular reflection over concave cylinders. Isr. J. Technol. 23, 71–74.Google Scholar
Ben-Dor, G., Takayama, K. & Kawauchi, T. 1980 The transition from regular to Mach reflexion and from Mach to regular reflexion in truly non-stationary flows. J. Fluid Mech. 100, 147–160.CrossRefGoogle Scholar
Bond, C., Hill, D. J., Meiron, D. I. & Dimotakis, P. E. 2009 Shock focusing in a planar convergent geometry: experiment and simulation. J. Fluid Mech. 641, 297–333.CrossRefGoogle Scholar
Britan, A., Elperin, T., Igra, O. & Jiang, J. P. 1995 Acceleration of a sphere behind planar shock waves. Exp. Fluids 20, 84–90.CrossRefGoogle Scholar
Geva, M., Ram, O. & Sadot, O. 2013 The non-stationary hysteresis phenomenon in shock wave reflections. J. Fluid Mech. 732, R1.CrossRefGoogle Scholar
Glazer, E., Sadot, O., Hadjadj, A. & Chaudhuri, A. 2011 Velocity scaling of a shock wave reflected off a circular cylinder. Phys. Rev. E 83, 066317.CrossRefGoogle Scholar
Gruber, S. & Skews, B. 2013 Weak shock wave reflection from concave surfaces. Exp. Fluids 54, 1–14.CrossRefGoogle Scholar
Gvozdeva, L. G., Lagutov, Y. P. & Fokeev, V. P. 1982 Transition from mach reflection to regular reflection when strong shock waves interact with cylindrical surfaces. Fluid Dyn. 17, 273–278.CrossRefGoogle Scholar
Hornung, H. G., Oertel, H. Jr. & Sandeman, R. J. 1979 Transition to Mach reflection of shock waves in steady and pseudo steady flow with and without relaxation. J. Fluid Mech. 90, 541–560.CrossRefGoogle Scholar
Itoh, S., Okazaki, N. & Itaya, M. 1981 On the transition between regular and Mach reflection in truly non-stationary flows. J. Fluid Mech. 108, 383–400.CrossRefGoogle Scholar
Johansson, B., Apazidis, N. & Lesser, M. B. 1999 On shock waves in a confined reflector. Wear 233–235, 79–85.CrossRefGoogle Scholar
Kjellander, M., Tillmark, N. & Apazidis, N. 2012 Energy concentration by spherical converging shocks generated in a shock tube. Phys. Fluids 24, 126103.CrossRefGoogle Scholar
Kleine, H., Timofeev, E., Hakkaki-Fard, A. & Skews, B. 2014 The influence of Reynolds number on the triple point trajectories at shock reflection off cylindrical surfaces. J. Fluid Mech. 740, 47–60.CrossRefGoogle Scholar
Naidoo, K.2011 Dynamic shock wave reflection phenomena. PhD thesis, University of Witwatersrand, Johannesburg, South Africa.Google Scholar
Naidoo, K. & Skews, B. W. 2011 Dynamic effects on the transition between two-dimensional regular and Mach reflection of shock waves in an ideal, steady supersonic free stream. J. Fluid Mech. 676, 432–460.CrossRefGoogle Scholar
Skews, B. 2005 Shock wave interaction with porous plates. Exp. Fluids 39, 875–884.CrossRefGoogle Scholar
Skews, B. W. 2008 A fresh look at unsteady shock wave reflection using high-speed imaging. In Proceedings SPIE 7126, 28th International Congress on High-Speed Imaging and Photonics, Canberra, Australia, Nov. 2008.Google Scholar
Skews, B. W. & Blitterswijk, A. 2011 Shock wave reflection off coupled surfaces. Shock Waves 21, 491–498.CrossRefGoogle Scholar
Skews, B. W. & Kleine, H. 2007 Flow features resulting from shock wave impact on a cylindrical cavity. J. Fluid Mech. 580, 481–493.CrossRefGoogle Scholar
Skews, B. & Kleine, H. 2009 Unsteady flow diagnostics using weak perturbations. Exp. Fluids 46, 65–76.CrossRefGoogle Scholar
Skews, B. W. & Kleine, H. 2010 Shock wave interaction with convex circular cylindrical surfaces. J. Fluid Mech. 654, 195–205.CrossRefGoogle Scholar
Sturtevant, B. & Kulkarny, V. A. 1976 The focusing of weak shock waves. J. Fluid Mech. 73, 651–671.CrossRefGoogle Scholar
Sun, M., Yada, K., Jagadeesh, G., Onodera, O., Ogawa, T. & Takayama, K. 2003 A study of shock wave interaction with a rotating cylinder. Shock Waves 12, 479–485.CrossRefGoogle Scholar
Takayama, K. & Ben-Dor, G. 1985 The inverse Mach reflection. AIAA J. 23 (12), 1853–1859.CrossRefGoogle Scholar
Takayama, K. & Sasaki, M. 1983 Effects of radius of curvature and initial angle on the shock transition over concave and convex walls. Rep. Inst. High Speed Mech. 46, 1–30.Google Scholar
Tanno, H., Itoh, K., Saito, T., Abe, A. & Takayama, K. 2003 Interaction of a shock with a sphere suspended in a vertical shock tube. Shock Waves 13, 191–200.CrossRefGoogle Scholar