Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-29T07:48:34.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat/mass transport in shear flow over a heterogeneous surface with first-order surface-reactive domains

Published online by Cambridge University Press:  08 October 2015

Preyas N. Shah Open the ORCID record for Preyas N. Shah [Opens in a new window]  and
Eric S. G. Shaqfeh
Preyas N. Shah
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA
Eric S. G. Shaqfeh*
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA Department of Chemical Engineering, Stanford University, Stanford, CA 94305, USA Institute of Computational and Mathematical Engineering, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Surfaces that include heterogeneous mass transfer at the microscale are ubiquitous in nature and engineering. Many such media are modelled via an effective surface reaction rate or mass transfer coefficient employing the conventional ansatz of kinetically limited transport at the microscale. However, this assumption is not always valid, particularly when there is strong flow. We are interested in modelling reactive and/or porous surfaces that occur in systems where the effective Damköhler number at the microscale can be 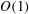$O(1)$ and the local Péclet number may be large. In order to expand the range of the effective mass transfer surface coefficient, we study transport from a uniform bath of species in an unbounded shear flow over a flat surface. This surface has a heterogeneous distribution of first-order surface-reactive circular patches (or pores). To understand the physics at the length scale of the patch size, we first analyse the flux to a single reactive patch. We use both analytic and boundary element simulations for this purpose. The shear flow induces a 3-D concentration wake structure downstream of the patch. When two patches are aligned in the shear direction, the wakes interact to reduce the per patch flux compared with the single-patch case. Having determined the length scale of the interaction between two patches, we study the transport to a periodic and disordered distribution of patches again using analytic and boundary integral techniques. We obtain, up to non-dilute patch area fraction, an effective boundary condition for the transport to the patches that depends on the local mass transfer coefficient (or reaction rate) and shear rate. We demonstrate that this boundary condition replaces the details of the heterogeneous surfaces at a wall-normal effective slip distance also determined for non-dilute patch area fractions. The slip distance again depends on the shear rate, and weakly on the reaction rate, and scales with the patch size. These effective boundary conditions can be used directly in large-scale physics simulations as long as the local shear rate, reaction rate and patch area fraction are known.

JFM classification

Low-Reynolds-number flows: Boundary integral methods Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 782 , 10 November 2015 , pp. 260 - 299
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartholomew, C. H. & Farrauto, R. J. 2011 Fundamentals of Industrial Catalytic Processes. John Wiley & Sons.Google Scholar
Bender, M. A. & Stone, H. A. 1993 An integral equation approach to the study of the steady state current at surface microelectrodes. J. Electroanalyt. Chem. 351 (1), 29–55.Google Scholar
Churchill, S. W. & Usagi, R. 1972 A general expression for the correlation of rates of transfer and other phenomena. AIChE J. 18 (6), 1121–1128.Google Scholar
Córdoba, A. 1989 Dirac comb. Lett. Math. Phys. 17 (3), 191–196.Google Scholar
Dudukovic, M. P. & Mills, P. L. 1985 A correction factor for mass transfer coefficients for transport to partially impenetrable or nonadsorbing surfaces. AIChE J. 31 (3), 491–494.CrossRefGoogle Scholar
Gupta, N., Gattrell, M. & MacDougall, B. 2006 Calculation for the cathode surface concentrations in the electrochemical reduction of $\text{CO}_{2}$ in $\text{KHCO}_{3}$ solutions. J. Appl. Electrochem. 36 (2), 161–172.Google Scholar
Hasimoto, H. 1959 On the periodic fundamental solutions of the Stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5 (02), 317–328.Google Scholar
Heinze, J. 1993 Ultramicroelectrodes in electrochemistry. Angew. Chem., Int. Ed. Engl. 32 (9), 1268–1288.CrossRefGoogle Scholar
Herskowitz, M., Carbonell, R. G. & Smith, J. M. 1979 Effectiveness factors and mass transfer in trickle-bed reactors. AIChE J. 25 (2), 272–283.CrossRefGoogle Scholar
Hill, R. J., Koch, D. L. & Ladd, A. J. C. 2001 The first effects of fluid inertia on flows in ordered and random arrays of spheres. J. Fluid Mech. 448, 213–241.CrossRefGoogle Scholar
Introini, C., Quintard, M. & Duval, F. 2011 Effective surface modeling for momentum and heat transfer over rough surfaces: application to a natural convection problem. Intl J. Heat Mass Transfer 54 (15), 3622–3641.Google Scholar
Juhasz, N. M. & Deen, W. M. 1991 Effect of local Peclet number on mass transfer to a heterogeneous surface. Ind. Engng Chem. Res. 30 (3), 556–562.Google Scholar
Juhasz, N. M. & Deen, W. M. 1993 Electrochemical measurements of mass transfer at surfaces with discrete reactive areas. AIChE J. 39 (10), 1708–1715.Google Scholar
Lambert, M. A. & Fletcher, L. S. 1993 Review of the thermal contact conductance of junctions with metallic coatings and films. J. Thermophys. Heat Transfer 7 (4), 547–554.CrossRefGoogle Scholar
Lévêque, M. A. 1928 The laws of heat transmission by convection. Les Annales des Mines: Memoires 12 (13), 201–299.Google Scholar
Lucas, S. K., Sipcic, R. & Stone, H. A. 1997 An integral equation solution for the steady-state current at a periodic array of surface microelectrodes. SIAM J. Appl. Maths 57 (6), 1615–1638.Google Scholar
Nanis, L. & Kesselman, W. 1971 Engineering applications of current and potential distributions in disk electrode systems. J. Electrochem. Soc. 118 (3), 454–461.Google Scholar
Phillips, C. G. 1990 Heat and mass transfer from a film into steady shear flow. Q. J. Mech. Appl. Maths 43 (1), 135–159.CrossRefGoogle Scholar
Reiss, L. P. & Hanratty, T. J. 1963 An experimental study of the unsteady nature of the viscous sublayer. AIChE J. 9 (2), 154–160.Google Scholar
Reller, H., Kirowa-Eisner, F. & Gileadi, E. 1982 Ensembles of microelectrodes: a digital-simulation. J. Electroanalyt. Chem. Interfacial Electrochem. 138 (1), 65–77.Google Scholar
Roberts, G. W. 1976 The influence of mass and heat transfer on the performance of heterogeneous catalysts in gas/liquid/solid systems. In Catalysis in Organic Synthesis (ed. Rylander, P. N. & Greenfield, H.), Academic Press.Google Scholar
Sadhal, S. S. & Tio, K. 1991 Analysis of thermal constriction resistance with adiabatic circular gaps. J. Thermophys. Heat Transfer 5 (4), 550–559.Google Scholar
Sangani, A. S. & Behl, S. 1989 The planar singular solutions of Stokes and Laplace equations and their application to transport processes near porous surfaces. Phys. Fluids A 1 (1), 21–37.CrossRefGoogle Scholar
Shah, P., Fitzgibbon, S., Narsimhan, V. & Shaqfeh, E. S. G. 2014 Singular perturbation theory for predicting extravasation of Brownian particles. J. Engng Maths 84 (1), 155–171.CrossRefGoogle ScholarPubMed
Smith, B. R., Kempen, P., Bouley, D., Xu, A., Liu, Z., Melosh, N., Dai, H., Sinclair, R. & Gambhir, S. S. 2012 Shape matters: intravital microscopy reveals surprising geometrical dependence for nanoparticles in tumor models of extravasation. Nano Lett. 12 (7), 3369–3377.Google Scholar
Stone, H. A. 1989 Heat/mass transfer from surface films to shear flows at arbitrary Peclet numbers. Phys. Fluids A 1 (7), 1112–1122.Google Scholar
Tio, K. & Sadhal, S. S. 1992 Thermal constriction resistance: effects of boundary conditions and contact geometries. Intl J. Heat Mass Transfer 35 (6), 1533–1544.Google Scholar
Veran, S., Aspa, Y. & Quintard, M. 2009 Effective boundary conditions for rough reactive walls in laminar boundary layers. Intl J. Heat Mass Transfer 52 (15), 3712–3725.Google Scholar
Wightman, R. M. & Wipf, D. O. 1989 Voltammetry at ultramicroelectrodes. Electroanalyt. Chem. 15, 267–353.Google Scholar
Xiang, C., Meng, A. C. & Lewis, N. S. 2012 Evaluation and optimization of mass transport of redox species in silicon microwire-array photoelectrodes. Proc. Natl Acad. Sci. USA 109 (39), 15622–15627.Google Scholar
Zhao, H. & Shaqfeh, E. S. G. 2011 Shear-induced platelet margination in a microchannel. Phys. Rev. E 83, 061924.Google Scholar