Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-22T14:04:51.801Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat transfer by rapidly rotating Rayleigh–Bénard convection

Published online by Cambridge University Press:  10 January 2012

E. M. King ,
S. Stellmach  and
J. M. Aurnou
E. M. King*
Affiliation:
Department of Earth and Planetary Science, University of California, Berkeley, CA 94720-4767, USA
S. Stellmach
Affiliation:
Institut für Geophysik, Westfälische Wilhelms-Universität Münster, Arbeitsgruppe Geodynamik, Corrensstraße 24, 48149 Münster, Germany
J. M. Aurnou
Affiliation:
Department of Earth and Space Sciences, University of California, Los Angeles, CA 90095-1567, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

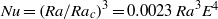Turbulent, rapidly rotating convection has been of interest for decades, yet there exists no generally accepted scaling law for heat transfer behaviour in this system. Here, we develop an exact scaling law for heat transfer by geostrophic convection, , by considering the stability of the thermal boundary layers, where , 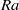and 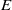are the Nusselt, Rayleigh and Ekman numbers, respectively, and 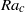is the critical Rayleigh number for the onset of convection. Furthermore, we use the scaling behaviour of the thermal and Ekman boundary layer thicknesses to quantify the necessary conditions for geostrophic convection: 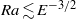. Interestingly, the predictions of both heat flux and regime transition do not depend on the total height of the fluid layer. We test these scaling arguments with data from laboratory and numerical experiments. Adequate agreement is found between theory and experiment, although there is a paucity of convection data for low .

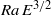JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 691 , 25 January 2012 , pp. 568 - 582
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
2. Amati, G., Koal, K., Massaioli, F., Sreenivasan, K. R. & Verzicco, R. 2005 Turbulent thermal convection at high Rayleigh numbers for a Boussinesq fluid of constant Prandtl number. Phys. Fluids 17, 121701.Google Scholar
3. Aurnou, J. 2007 Planetary core dynamics and convective heat transfer scaling. Geophys. Astrophys. Fluid Dyn. 101 (5–6), 327–345.Google Scholar
4. Belmonte, A., Tilgner, A. & Libchaber, A. 1993 Boundary layer length scales in thermal turbulence. Phys. Rev. Lett. 70 (26), 4067–4070.CrossRefGoogle ScholarPubMed
5. Belmonte, A., Tilgner, A. & Libchaber, A. 1994 Temperature and velocity boundary layers in turbulent convection. Phys. Rev. E 50 (1), 269–280.Google Scholar
6. Boubnov, B. & Golitsyn, G. 1990 Temperature and velocity-field regimes of convective motions in a rotating plane fluid layer. J. Fluid Mech. 219, 215–239.CrossRefGoogle Scholar
7. Canuto, V. & Dubovikov, M. 1998 Two scaling regimes for rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 80 (2), 281–284.CrossRefGoogle Scholar
8. Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X. Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
9. Chan, S.-K. 1974 Investigation of turbulent convection under a rotational constraint. J. Fluid Mech. 64 (3), 477–506.Google Scholar
10. Chandrasekhar, S. 1953 The instability of a layer of fluid heated below and subject to Coriolis forces. Proc. R. Soc. Lond. A 217 (1130), 306–327.Google Scholar
11. Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon Press.Google Scholar
12. Chilla, F., Ciliberto, S., Innocenti, C. & Pampaloni, E. 1993 Boundary layer and scaling properties in turbulent thermal convection. Il Nuovo Cimento D 15D (9), 1229–1249.Google Scholar
13. Christensen, U. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Intl 166 (1), 97–114.CrossRefGoogle Scholar
14. Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.Google Scholar
15. Glazier, J., Segawa, T., Naert, A. & Sano, M. 1999 Evidence against ‘ultrahard’ thermal turbulence at very high Rayleigh numbers. Nature 398, 307–310.CrossRefGoogle Scholar
16. Greenspan, H. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
17. Hartlep, T. 2004 Strukturbildung und Turbulenz. Eine numerische Studie zur turbulenten Rayleigh–Bénard Konvektion. PhD thesis, Mathematisch-Naturwissenschaftliche Fakultät, Universität Göttingen.Google Scholar
18. Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.Google Scholar
19. King, E., Soderlund, K., Christensen, U. R., Wicht, J. & Aurnou, J. M. 2010 Convective heat transfer in planetary dynamo models. Geochem. Geophys. Geosyst. 11 (6), Q06016.Google Scholar
20. King, E., Stellmach, S., Noir, J., Hansen, U. & Aurnou, J. 2009 Boundary layer control of rotating convection systems. Nature 457 (7227), 301–304.Google Scholar
21. Kunnen, R. P. J., Geurts, B. J. & Clercx, H. J. H. 2006 Direct numerical simulation of turbulent rotating Rayleigh–Bénard convection. In Direct and Large-Eddy Simulation VI, 12–14 September 2005, Poitiers, France, ERCOFTAC Ser. , 10. pp. 233–240. Springer.Google Scholar
22. Liu, Y. M. & Ecke, R. E. 1997 Heat transport scaling in turbulent Rayleigh–Bénard convection: effects of rotation and Prandtl number. Phys. Rev. Lett. 79 (12), 2257–2260.Google Scholar
23. Liu, Y. & Ecke, R. E. 1999 Nonlinear travelling waves in rotating Rayleigh–Bénard convection: stability boundaries and phase diffusion. Phys. Rev. E 59 (4), 4091–4105.Google Scholar
24. Liu, Y. & Ecke, R. 2009 Heat transport measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 80 (3), 6314–6325.CrossRefGoogle ScholarPubMed
25. Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225 (1161), 196–212.Google Scholar
26. Niemela, J. J. & Sreenivasan, K. R. 2006 Turbulent convection at high Rayleigh numbers and aspect ratio 4. J. Fluid Mech. 557, 411–422.CrossRefGoogle Scholar
27. Pellew, A. & Southwell, R. 1940 On maintained convective motion in a fluid heated from below. Proc. R. Soc. Lond. A 176, 312–343.Google Scholar
28. Priestley, C. 1954 Convection from a large horizontal surface. Austral. J. Phys. 7, 176–202.Google Scholar
29. Riahi, N. 1977 Upper-bound problem for a rotating system. J. Fluid Mech. 81 (3), 523–528.Google Scholar
30. Rossby, H. 1969 A study of Bénard convection with and without rotation. J. Fluid Mech. 36 (2), 309–335.Google Scholar
31. Sakai, S. 1997 The horizontal scale of rotating convection in the geostrophic regime. J. Fluid Mech. 333, 85–95.Google Scholar
32. Schmitz, S. & Tilgner, A. 2009 Heat transport in rotating convection without Ekman layers. Phys. Rev. E 80 (1), 5305–5307.Google Scholar
33. Schmitz, S. & Tilgner, A. 2010 Transitions in turbulent rotating Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 104 (5–6), 481–489.CrossRefGoogle Scholar
34. Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.CrossRefGoogle Scholar
35. Spiegel, E. 1971 Convection in stars. I. Basic Boussinesq convection. Annu. Rev. Astron. Astrophys. 9, 323–352.Google Scholar
36. Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.Google Scholar
37. Stellmach, S. & Hansen, U. 2004 Cartesian convection-driven dynamos at low Ekman number. Phys. Rev. E 70, 056312.CrossRefGoogle ScholarPubMed
38. Sun, C., Cheung, Y. H & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
39. Zhong, F., Ecke, R. E. & Steinberg, V. 1993 Rotating Rayleigh–Bénard convection: asymmetric modes and vortex states. J. Fluid Mech. 249, 135–159.Google Scholar
40. Zhong, J., Stevens, R. & Clercx, H. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.Google Scholar
Supplementary material: PDF

King et al. supplementary material

Supplementary material

Download King et al. supplementary material(PDF)
PDF 1.5 MB