Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T21:10:06.422Z Has data issue: false hasContentIssue false
  • English
  • Français

Group resonant interactions between surface and internal gravity waves in a two-layer system

Published online by Cambridge University Press:  02 April 2020

Tore Magnus A. Taklo  and
Wooyoung Choi Open the ORCID record for Wooyoung Choi [Opens in a new window]
Tore Magnus A. Taklo
Affiliation:
Department of Mathematical Sciences, New Jersey Institute of Technology, Newark,NJ 07102-1982, USA
Wooyoung Choi*
Affiliation:
Department of Mathematical Sciences, New Jersey Institute of Technology, Newark,NJ 07102-1982, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

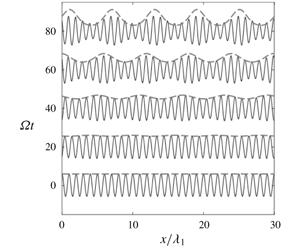
Nonlinear interactions between surface and internal gravity waves in a two-layer system are studied using explicit second-order nonlinear evolution equations in Hamiltonian form. Motivated by the detailed experiment of Lewis, Lake & Ko (J. Fluid Mech., vol. 63, 1974, pp. 773–800), our focus is on surface wave modulation by the group resonance mechanism that corresponds to near-resonant triad interactions between a long internal wave and short surface waves. Our numerical solutions show good agreement with laboratory measurements of the local wave amplitude and slope, and confirm that the surface modulation becomes significant when the group velocity of the surface waves matches the phase speed of the internal wave, as the linear modulation theory predicts. It is shown, however, that, after the envelope amplitude is increased sufficiently, the surface and internal waves start to exchange energy through near-resonant triad interactions, which is found to be crucial to accurately describe the long-term surface wave modulation by an internal wave. The reduced amplitude equations are also adopted to validate this observation. For oceanic applications, numerical solutions are presented for a density ratio close to one and it is found that significant energy exchanges occur through primary and successive resonant triad interactions.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows Waves/Free-surface Flows: Surface gravity waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 892 , 10 June 2020 , A14
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M.-R. 2012 A new triad resonance between co-propagating surface and interfacial waves. J. Fluid Mech. 691, 267–278.CrossRefGoogle Scholar
Alam, M.-R., Liu, Y. & Yue, D. K. P. 2009 Bragg resonance of waves in a two-layer fluid propagating over bottom ripples. Part II. Numerical simulation. J. Fluid Mech. 624, 225–253.CrossRefGoogle Scholar
Alpers, W. 1985 Theory of radar imaging of internal waves. Nature 314, 245–247.CrossRefGoogle Scholar
Ball, F. K. 1964 Energy transfer between external and internal gravity waves. J. Fluid Mech. 19, 465–478.CrossRefGoogle Scholar
Benjamin, T. B. & Bridges, T. J. 1997 Reappraisal of the Kelvin-Helmholtz problem. Part 1. Hamiltonian structure. J. Fluid Mech. 333, 301–325.CrossRefGoogle Scholar
Benney, D. J. 1977 A general theory for interactions between short and long waves. Stud. Appl. Maths 56, 81–94.CrossRefGoogle Scholar
Bretherton, F. P. & Garrett, C. J. R. 1969 Wavetrains in inhomogeneous moving media. Proc. R. Soc. Lond. A 302, 529–554.Google Scholar
Choi, W. 1995 Nonlinear evolution equations for two-dimensional surface waves in a fluid of finite depth. J. Fluid Mech. 295, 381–394.CrossRefGoogle Scholar
Choi, W., Chabane, M. & Taklo, T. M. A. 2020 Two-dimensional resonant triad interactions in a two-layer system. J. Fluid Mech. (submitted).Google Scholar
Choi, W. & Lyzenga, D. R. 2006 Nonlinear surface wave dynamics in slowly varying ocean environments. In Proceedings of the 26th Symposium on Naval Hydrodynamics, Rome, Italy, pp. 1–9.Google Scholar
Craig, W., Guyenne, P. & Kalisch, H. 2005 Hamiltonian long-wave expansions for free surfaces and interfaces. Commun. Pure Appl. Maths 58, 1587–1641.CrossRefGoogle Scholar
Craig, W., Guyenne, P. & Sulem, C. 2012 The surface signature of internal waves. J. Fluid Mech. 710, 277–303.CrossRefGoogle Scholar
Ewing, G. 1950 Slicks, surface films and internal waves. J. Mar. Res. 9, 161–187.Google Scholar
Funakoshi, M. & Oikawa, M. 1983 The resonant interaction between a long internal gravity wave and a surface gravity wave packet. J. Phys. Soc. Japan 52, 1982–1995.CrossRefGoogle Scholar
Gargett, A. E. & Hughes, B. A. 1972 On the interaction of surface and internal waves. J. Fluid Mech. 52, 179–191.CrossRefGoogle Scholar
Gasparovic, R. F., Apel, J. R. & Kasischke, E. S. 1988 An overview of the SAR internal wave experiment. J. Geophys. Res. 93, 12304–12315.CrossRefGoogle Scholar
Hill, D. F. & Foda, M. A. 1996 Subharmonic resonance of short internal standing waves by progressive surface waves. J. Fluid Mech. 321, 217–233.CrossRefGoogle Scholar
Hughes, B. A. 1978 The effect of internal waves on surface wind waves 2. Theoretical analysis. J. Geophys. Res. 83, 455–465.CrossRefGoogle Scholar
Hughes, B. A. & Grant, H. L. 1978 The effect of internal waves on surface wind waves 1. Experimental measurements. J. Geophys. Res. 83, 443–454.CrossRefGoogle Scholar
Hwung, H.-H., Yang, R.-Y. & Shugan, I. V. 2009 Exposure of internal waves on the sea surface. J. Fluid Mech. 626, 1–20.CrossRefGoogle Scholar
Jiang, S. W., Kovacic, G., Zhou, D. & Cai, D. 2019 Modulation-resonance mechanism for surface waves in a two-layer fluid system. J. Fluid Mech. 875, 807–841.CrossRefGoogle Scholar
Jo, T.-C. & Choi, W. 2008 On stabilizing the strongly nonlinear internal wave model. Stud. Appl. Maths 120, 65–85.CrossRefGoogle Scholar
Kawahara, T., Sugimoto, N. & Kakutani, T. 1975 Nonlinear interaction between short and long capillary-gravity waves. J. Phys. Soc. Japan 39, 1379–1386.CrossRefGoogle Scholar
Kodaira, T., Waseda, T., Miyata, M. & Choi, W. 2016 Internal solitary waves in a two-fluid system with a free surface. J. Fluid Mech. 804, 201–223.CrossRefGoogle Scholar
LaFond, E. C. 1962 Internal waves, Part I in N. M. Hill, The Sea. Interscience 1, 731–751.Google Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Dover.Google Scholar
Lewis, J. E., Lake, B. M. & Ko, D. R. S. 1974 On the interaction of internal waves and surface gravity waves. J. Fluid Mech. 63, 773–800.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Stewart, R. W. 1960 Changes in the form of short gravity waves on long waves and tidal currents. J. Fluid Mech. 8, 565–583.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Stewart, R. W. 1961 The change in amplitude of short gravity waves on steady non-uniform currents. J. Fluid Mech. 10, 529–549.CrossRefGoogle Scholar
McGoldrick, L. F. 1965 Resonant interactions among capillary-gravity waves. J. Fluid Mech. 21, 305–331.CrossRefGoogle Scholar
Osborne, A. R. & Burch, T. L. 1980 Internal solitons in the Andaman sea. Science 208, 451–460.CrossRefGoogle ScholarPubMed
Phillips, O. M. 1960 On the dynamics of unsteady gravity waves of finite amplitude. Part 1. The elementary interactions. J. Fluid Mech. 9, 193–217.CrossRefGoogle Scholar
Phillips, O. M. 1977 Dynamics of the Upper Ocean Layer. John Wiley & Sons.Google Scholar
Segur, H. 1980 Resonant interactions of surface and internal gravity waves. Phys. Fluids Res. Notes 23, 2556–2557.CrossRefGoogle Scholar
Tanaka, M. & Wakayama, K. 2015 A numerical study on the energy transfer from surface waves to interfacial waves in a two-layer fluid system. J. Fluid Mech. 763, 202–217.CrossRefGoogle Scholar
Thorpe, S. A. 1968 On the shape of progressive internal waves. Phil. Trans. R. Soc. Lond. A 263, 563–614.Google Scholar
Watson, G. & Robinson, I. S. 1990 A study of internal wave propagation in the strait of Gibraltar using shore-based marine radar images. J. Phys. Oceanogr. 20, 374–395.2.0.CO;2>CrossRefGoogle Scholar
Wen, F. 1995 Resonant generation of internal waves on the soft sea bed by a surface water wave. Phys. Fluids 7, 1915–1922.CrossRefGoogle Scholar
Whitham, G. B. 1962 Mass, momentum and energy flux in water waves. J. Fluid Mech. 12, 135–147.CrossRefGoogle Scholar