Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T16:25:22.547Z Has data issue: false hasContentIssue false
  • English
  • Français

Geostrophic adjustment in a closed basin with islands

Published online by Cambridge University Press:  05 December 2013

E. R. Johnson  and
R. H. J. Grimshaw
E. R. Johnson*
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK
R. H. J. Grimshaw
Affiliation:
Department of Mathematical Sciences, Loughborough University, LE11 3TU, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the geostrophic adjustment of a density-stratified fluid in a basin of constant depth on an 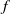$f$-plane in the context of linearized theory. For a single vertical mode, the equations are equivalent to those for a linearized shallow-water theory for a homogeneous fluid. Associated with any initial state there is a unique steady geostrophically adjusted component of the flow compatible with the initial conditions. This steady component gives the time average of the flow and is analogous to the adjusted flow in an unbounded domain without islands. The remainder of the response consists of superinertial Poincaré and subinertial Kelvin wave modes and expressions for the energy partition between the modes in arbitrary basins again follow directly from the initial conditions. The solution for an arbitrary initial density distribution released from rest in a circular domain is found in closed form. When the Rossby radius is much smaller than the basin radius, appropriate for the baroclinic modes, the interior adjusted solution is close to that of the initial state, except for small-amplitude trapped Poincaré waves, while Kelvin waves propagate around the boundaries, carrying, without change of form, the deviation of the initial height field from its average.

JFM classification

Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Topographic effects Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 738 , 10 January 2014 , pp. 358 - 377
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Fornberg, B. 1995 A pseudospectral approach for polar and spherical geometries. SIAM J. Sci. Comput. 16, 1071–1081.Google Scholar
Gill, A. E. 1976 Adjustment under gravity in a rotating channel. J. Fluid Mech. 77, 603–621.Google Scholar
Gill, A. E. 1982 Atmosphere–Ocean Dynamics. Academic.Google Scholar
Goldstein, S. 1929 Tidal motion in a rotating elliptic basin of constant depth. Mon. Not. R. Astron. Soc. Geophys. Suppl. 2, 213–231.Google Scholar
Gomez-Giraldo, A., Imberger, J. & Antenucci, J. P. 2006 Spatial structure of the dominant basin-scale internal waves in Lake Kinneret. Limnol. Oceanogr. 51, 229–246.Google Scholar
Greenspan, H. P. 1965 On the general theory of contained rotating fluid motions. J. Fluid Mech. 22, 449–462.Google Scholar
Hermann, A. J., Rhines, P. B. & Johnson, E. R. 1989 Nonlinear Rossby adjustment in a channel – beyond Kelvin waves. J. Fluid Mech. 205, 469–502.Google Scholar
Hughes, C. W., Meredith, M. P. & Heywood, K. J. 1999 Wind-driven transport fluctuations through Drake Passage: a southern mode. J. Phys. Oceanogr. 29, 1971–1992.Google Scholar
Johnson, E. R. 1989 Scattering of shelf waves by islands. J. Phys. Oceanogr. 19, 1311–1316.Google Scholar
Kamenkovich, V. M. 1961 The integration of the marine current theory equations in multiply connected regions. Dokl. – Acad. Sci. USSR Earth Sci. Sec. 138, 629–631.Google Scholar
Kusahara, K. & Ohshima, K. I. 2009 Dynamics of the wind-driven sea level variation around Antarctica. J. Phys. Oceanogr. 39, 658–674.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Lin, C. C. 1941 On the motion of vortices in two-dimensions. I. Existence of the Kirchhoff–Routh function. Proc. Natl Acad. Sci. 27, 570–577.Google Scholar
Luneva, M. V., Willmott, A. J. & Maqueda, M. A. M. 2012 Geostrophic adjustment problems in a polar basin. Atmos.-Ocean 50, 134–155.Google Scholar
Meredith, M. P., Woodworth, P. L., Chereskin, T. K., Marshall, D. P., Allison, L. C., Bigg, G. R., Donohue, K., Heywood, K. J., Hughes, C. W., Hibbert, A., Hogg, A. McC., Johnson, H. L., Jullion, L., King, B. A., Leach, H., Lenn, Y.-D., Morales Maqueda, M. A., Munday, D. R., Naveira Garabato, A. C., Provost, C., Sallée, J.-B. & Sprintall, J. 2011 Sustained monitoring of the southern ocean at Drake Passage: past achievements and future priorities. Rev. Geophys. 49, RG4005.Google Scholar
Meredith, M. P., Woodworth, P. L., Hughes, C. W. & Stepanov, V. 2004 Changes in the ocean transport through Drake Passage during the 1980s and 1990s, forced by changes in the Southern Annular Mode. Geophys. Res. Lett. 31, L21305.Google Scholar
Peterson, R. G. 1988 On the transport of the Antarctic Circumpolar Current through Drake Passage and its relation to wind. J. Geophys. Res.-Oceans 93, 13993–14004.Google Scholar
Platzman, G. W. 1972 Two-dimensional free oscillations in natural basins. J. Phys. Oceanogr. 2, 117–138.Google Scholar
Proudman, J. 1929 On a general expansion in the theory of the tides. Proc. Lond. Math. Soc. 29, 527–536.CrossRefGoogle Scholar
Rhines, P. B. 1969 Slow oscillations in an ocean of varying depth. 2. Islands and seamounts. J. Fluid Mech. 37, 191–205.Google Scholar
Rossby, C. G. 1938 On the mutual adjustment of pressure and velocity distributions in certain simple current systems, II. J. Mar. Res. 1, 239–263.Google Scholar
Stocker, R. & Imberger, J. 2003 Energy partitioning and horizontal dispersion in the surface layer of a stratified lake. J. Phys. Ocean. 33, 512–529.Google Scholar
Timmermans, M. L., Rainville, L., Thomas, L. & Proshutinsky, A. 2010 Moored observations of bottom-intensified motions in the deep Canada Basin, Arctic Ocean. J. Mar. Res. 68, 625–641.Google Scholar
Wake, G. W., Hopfinger, E. J. & Ivey, G. N. 2007 Experimental study on resonantly forced interfacial waves in a stratified circular cylindrical basin. J. Fluid Mech. 582, 203–222.CrossRefGoogle Scholar
Wake, G. W., Ivey, G. N., Imberger, J. & McDonald, N. R. 2005 The temporal evolution of a geostrophic flow in a rotating stratified basin. Dyn. Atmos. Oceans 39, 189–210.Google Scholar
Wake, G. W., Ivey, G. N., Imberger, J., McDonald, N. R. & Stocker, R. 2004 Baroclinic adjustment in a rotating circular basin. J. Fluid Mech. 515, 63–86.CrossRefGoogle Scholar
Weijer, W. & Gille, S. T. 2005 Adjustment of the Southern Ocean to wind forcing on synoptic time scales. J. Phys. Oceanogr. 35, 2076–2089.Google Scholar

Johnson supplementary movie

The two-dimensional surface elevation evolution corresponding to figure 5 of the main text. The Chebyshev computational grid is marked on the surface.

Download Johnson supplementary movie(Video)
Video 9.9 MB
Supplementary material: PDF

Johnson supplementary material

Figures

Download Johnson supplementary material(PDF)
PDF 4.4 MB