Published online by Cambridge University Press: 21 July 2017
Cauchy invariants are now viewed as a powerful tool for investigating the Lagrangian structure of three-dimensional (3D) ideal flow (Frisch & Zheligovsky, Commun. Math. Phys., vol. 326, 2014, pp. 499–505; Podvigina et al., J. Comput. Phys., vol. 306, 2016, pp. 320–342). Looking at such invariants with the modern tools of differential geometry and of geodesic flow on the space SDiff of volume-preserving transformations (Arnold, Ann. Inst. Fourier, vol. 16, 1966, pp. 319–361), all manners of generalisations are here derived. The Cauchy invariants equation and the Cauchy formula, relating the vorticity and the Jacobian of the Lagrangian map, are shown to be two expressions of this Lie-advection invariance, which are duals of each other (specifically, Hodge dual). Actually, this is shown to be an instance of a general result which holds for flow both in flat (Euclidean) space and in a curved Riemannian space: any Lie-advection invariant 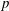 $p$-form which is exact (i.e. is a differential of a
$p$-form which is exact (i.e. is a differential of a 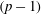 $(p-1)$-form) has an associated Cauchy invariants equation and a Cauchy formula. This constitutes a new fundamental result in linear transport theory, providing a Lagrangian formulation of Lie advection for some classes of differential forms. The result has a broad applicability: examples include the magnetohydrodynamics (MHD) equations and various extensions thereof, discussed by Lingam et al. (Phys. Lett. A, vol. 380, 2016, pp. 2400–2406), and include also the equations of Tao (2016, arXiv:1606.08481 [math.AP]), Euler equations with modified Biot–Savart law, displaying finite-time blow-up. Our main result is also used for new derivations, and several new results, concerning local helicity-type invariants for fluids and MHD flow in flat or curved spaces of arbitrary dimension.
$(p-1)$-form) has an associated Cauchy invariants equation and a Cauchy formula. This constitutes a new fundamental result in linear transport theory, providing a Lagrangian formulation of Lie advection for some classes of differential forms. The result has a broad applicability: examples include the magnetohydrodynamics (MHD) equations and various extensions thereof, discussed by Lingam et al. (Phys. Lett. A, vol. 380, 2016, pp. 2400–2406), and include also the equations of Tao (2016, arXiv:1606.08481 [math.AP]), Euler equations with modified Biot–Savart law, displaying finite-time blow-up. Our main result is also used for new derivations, and several new results, concerning local helicity-type invariants for fluids and MHD flow in flat or curved spaces of arbitrary dimension.