Article contents
A general self-preservation analysis for decaying homogeneous isotropic turbulence
Published online by Cambridge University Press: 21 May 2015
Abstract
A general framework of self-preservation (SP) is established, based on the transport equation of the second-order longitudinal velocity structure function in decaying homogeneous isotropic turbulence (HIT). The analysis introduces the skewness of the longitudinal velocity increment, 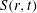 $S(r,t)$ (
$S(r,t)$ ( $r$ and
$r$ and  $t$ are space increment and time), as an SP controlling parameter. The present SP framework allows a critical appraisal of the specific assumptions that have been made in previous SP analyses. It is shown that SP is achieved when
$t$ are space increment and time), as an SP controlling parameter. The present SP framework allows a critical appraisal of the specific assumptions that have been made in previous SP analyses. It is shown that SP is achieved when 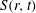 $S(r,t)$ varies in a self-similar manner, i.e.
$S(r,t)$ varies in a self-similar manner, i.e. 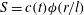 $S=c(t){\it\phi}(r/l)$ where
$S=c(t){\it\phi}(r/l)$ where 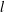 $l$ is a scaling length, and
$l$ is a scaling length, and 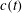 $c(t)$ and
$c(t)$ and 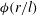 ${\it\phi}(r/l)$ are dimensionless functions of time and
${\it\phi}(r/l)$ are dimensionless functions of time and 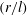 $(r/l)$, respectively. When
$(r/l)$, respectively. When 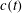 $c(t)$ is constant,
$c(t)$ is constant, 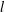 $l$ can be identified with the Kolmogorov length scale
$l$ can be identified with the Kolmogorov length scale 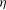 ${\it\eta}$, even when the Reynolds number is relatively small. On the other hand, the Taylor microscale
${\it\eta}$, even when the Reynolds number is relatively small. On the other hand, the Taylor microscale 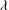 ${\it\lambda}$ is a relevant SP length scale only when certain conditions are met. The decay law for the turbulent kinetic energy (
${\it\lambda}$ is a relevant SP length scale only when certain conditions are met. The decay law for the turbulent kinetic energy (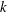 $k$) ensuing from the present SP is a generalization of the existing laws and can be expressed as
$k$) ensuing from the present SP is a generalization of the existing laws and can be expressed as 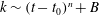 $k\sim (t-t_{0})^{n}+B$, where
$k\sim (t-t_{0})^{n}+B$, where  $B$ is a constant representing the energy of the motions whose scales are excluded from the SP range of scales. When
$B$ is a constant representing the energy of the motions whose scales are excluded from the SP range of scales. When 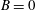 $B=0$, SP is achieved at all scales of motion and
$B=0$, SP is achieved at all scales of motion and 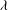 ${\it\lambda}$ becomes a relevant scaling length together with
${\it\lambda}$ becomes a relevant scaling length together with 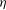 ${\it\eta}$. The analysis underlines the relation between the initial conditions and the power-law exponent
${\it\eta}$. The analysis underlines the relation between the initial conditions and the power-law exponent  $n$ and also provides a link between them. In particular, an expression relating
$n$ and also provides a link between them. In particular, an expression relating  $n$ to the initial values of the scaling length and velocity is developed. Finally, the present SP analysis is consistent with both experimental grid turbulence data and the eddy-damped quasi-normal Markovian numerical simulation of decaying HIT by Meldi & Sagaut (J. Turbul., vol. 14, 2013, pp. 24–53).
$n$ to the initial values of the scaling length and velocity is developed. Finally, the present SP analysis is consistent with both experimental grid turbulence data and the eddy-damped quasi-normal Markovian numerical simulation of decaying HIT by Meldi & Sagaut (J. Turbul., vol. 14, 2013, pp. 24–53).
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 18
- Cited by



