Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T14:12:59.290Z Has data issue: false hasContentIssue false
  • English
  • Français

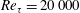Fully resolved measurements of turbulent boundary layer flows up to $Re_{\unicode[STIX]{x1D70F}}=20\,000$

Published online by Cambridge University Press:  20 July 2018

M. Samie Open the ORCID record for M. Samie [Opens in a new window] ,
I. Marusic ,
N. Hutchins ,
M. K. Fu Open the ORCID record for M. K. Fu [Opens in a new window] ,
Y. Fan ,
M. Hultmark  and
A. J. Smits
M. Samie*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
I. Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
N. Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
M. K. Fu
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Y. Fan
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
M. Hultmark
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
A. J. Smits
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

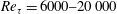Fully resolved measurements of turbulent boundary layers are reported for the Reynolds number range $Re_{\unicode[STIX]{x1D70F}}=6000{-}20\,000$. Despite several decades of research in wall-bounded turbulence there is still controversy over the behaviour of streamwise turbulence intensities near the wall, especially at high Reynolds numbers. Much of it stems from the uncertainty in measurement due to finite spatial resolution. Conventional hot-wire anemometry is limited for high Reynolds number measurements due to limited spatial resolution issues that cause attenuation in the streamwise turbulence intensity profile near the wall. To address this issue we use the nano-scale thermal anemometry probe (NSTAP), developed at Princeton University to conduct velocity measurements in the high Reynolds number boundary layer facility at the University of Melbourne. The NSTAP has a sensing length almost one order of magnitude smaller than conventional hot-wires. This enables us to acquire fully resolved velocity measurements of turbulent boundary layers up to 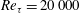$Re_{\unicode[STIX]{x1D70F}}=20\,000$. Results show that in the near-wall region, the viscous-scaled streamwise turbulence intensity grows with 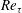$Re_{\unicode[STIX]{x1D70F}}$ in the Reynolds number range of the experiments. A second outer peak in the streamwise turbulence intensity is also shown to emerge at the highest Reynolds numbers. Moreover, the energy spectra in the near-wall region show excellent inner scaling over the small to moderate wavelength range, followed by a large-scale influence that increases with Reynolds number. Outer scaling in the outer region is found to collapse the energy spectra over high wavelengths across various Reynolds numbers.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 391 - 415
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfredsson, P. H., Segalini, A. & Örlü, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the ‘outer’ peak. Phys. Fluids 23 (4), 041702.Google Scholar
Baars, W. J., Squire, D. T., Talluru, K. M., Abbassi, M. R., Hutchins, N. & Marusic, I. 2016 Wall-drag measurements of smooth- and rough-wall turbulent boundary layers using a floating element. Exp. Fluids 57 (5), 90.Google Scholar
Bailey, S. C. C., Kunkel, G. J., Hultmark, M., Vallikivi, M., Hill, J. P., Meyer, K. A., Tsay, C., Arnold, C. B. & Smits, A. J. 2010 Turbulence measurements using a nanoscale thermal anemometry probe. J. Fluid Mech. 663, 160–179.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.Google Scholar
Chin, C. C., Hutchins, N., Ooi, A. & Marusic, I. 2009 Use of direct numerical simulation (DNS) data to investigate spatial resolution issues in measurements of wall-bounded turbulence. Meas. Sci. Technol. 20 (11), 115401.Google Scholar
Chin, C. C., Hutchins, N., Ooi, A. & Marusic, I. 2011 Spatial resolution correction for hot-wire anemometry in wall turbulence. Exp. Fluids 50 (5), 1443–1453.Google Scholar
Chin, C. C., Monty, J. P. & Ooi, A. 2014 Reynolds number effects in DNS of pipe flow and comparison with channels and boundary layers. Intl J. Heat Fluid Flow 45, 33–40.Google Scholar
Coleman, H. W & Steele, W. G. 2009 Experimentation, Validation, and Uncertainty Analysis for Engineers. Wiley.Google Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Fernholz, H. H. & Finley, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32 (4), 245–311.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.Google Scholar
Hultmark, M. & Smits, A. J. 2010 Temperature corrections for constant temperature and constant current hot-wire anemometers. Meas. Sci. Technol. 21 (10), 105404.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 094501.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. P. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Klewicki, J. C. & Falco, R. E. 1990 On accurately measuring statistics associated with small-scale structure in turbulent boundary layers using hot-wire probes. J. Fluid Mech. 219, 119–142.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5 (6), 407–417.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26 (1), 011702.Google Scholar
Marusic, I., Baars, W. J. & Hutchins, N. 2017 Scaling of the streamwise turbulence intensity in the context of inner–outer interactions in wall turbulence. Phys. Rev. Fluids 2 (10), 100502.Google Scholar
Marusic, I., Chauhan, K. A., Kulandaivelu, V. & Hutchins, N. 2015 Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 783, 379–411.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010b Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2010 Scaling of inner and outer regions for flat plate boundary layers. In Proceedings of the 17th Australasian Fluid Mechanics Conference, Auckland, New Zealand, pp. 5–9.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13 (3), 692–701.Google Scholar
Metzger, M. M., Klewicki, J. C., Bradshaw, K. L. & Sadr, R. 2001 Scaling the near-wall axial turbulent stress in the zero pressure gradient boundary layer. Phys. Fluids 13 (6), 1819–1821.Google Scholar
Metzger, M. M., McKeon, B. J. & Holmes, H. 2007 The near-neutral atmospheric surface layer: turbulence and non-stationarity. Phil. Trans. R. Soc. Lond. A 365 (1852), 859–876.Google Scholar
Miller, M. A., Estejab, B. & Bailey, S. C. C. 2014 Evaluation of hot-wire spatial filtering corrections for wall turbulence and correction for end-conduction effects. Exp. Fluids 55 (5), 1735.Google Scholar
Mochizuki, S. & Nieuwstadt, F. T. M. 1996 Reynolds-number-dependence of the maximum in the streamwise velocity fluctuations in wall turbulence. Exp. Fluids 21 (3), 218–226.Google Scholar
Monkewitz, P. A., Duncan, R. D. & Nagib, H. M. 2010 Correcting hot-wire measurements of stream-wise turbulence intensity in boundary layers. Phys. Fluids 22 (9), 091701.Google Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k 1 -1 law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95 (7), 074501.Google Scholar
Örlü, R., Fiorini, T., Segalini, A., Bellani, G., Talamelli, A. & Alfredsson, P. H. 2017 Reynolds stress scaling in pipe flow turbulence: first results from CICLoPE. Phil. Trans. R. Soc. Lond. A 375 (2089), 20160187.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Philip, J., Hutchins, N., Monty, J. P. & Marusic, I. 2013 Spatial averaging of velocity measurements in wall-bounded turbulence: single hot-wires. Meas. Sci. Technol. 24 (11), 115301.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34 (1), 349–374.Google Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Segalini, A., Örlü, R., Schlatter, P., Alfredsson, P. H., Rüedi, J.-D. & Talamelli, A. 2011 A method to estimate turbulence intensity and transverse Taylor microscale in turbulent flows from spatially averaged hot-wire data. Exp. Fluids 51 (3), 693.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25 (10), 105102.Google Scholar
Smits, A. J., Monty, J. P., Hultmark, M., Bailey, S. C. C., Hutchins, N. & Marusic, I. 2011 Spatial resolution correction for wall-bounded turbulence measurements. J. Fluid Mech. 676, 41–53.Google Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7 (11), 2778–2784.Google Scholar
Talamelli, A., Persiani, F., Fransson, J. H. M., Alfredsson, P. H., Johansson, A. V., Nagib, H. M., Rüedi, J.-D., Sreenivasan, K. R. & Monkewitz, P. A. 2009 CICLoPE: a response to the need for high Reynolds number experiments. Fluid Dyn. Res. 41 (2), 021407.Google Scholar
Talamelli, A., Segalini, A., Örlü, R., Schlatter, P. & Alfredsson, P. H. 2013 Correcting hot-wire spatial resolution effects in third- and fourth-order velocity moments in wall-bounded turbulence. Exp. Fluids 54 (4), 1496.Google Scholar
Talluru, K. M., Kulandaivelu, V., Hutchins, N. & Marusic, I. 2014 A calibration technique to correct sensor drift issues in hot-wire anemometry. Meas. Sci. Technol. 25 (10), 105304.Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. A 164, 476–490.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vallikivi, M., Ganapathisubramani, B. & Smits, A. J. 2015a Spectral scaling in boundary layers and pipes at very high Reynolds numbers. J. Fluid Mech. 771, 303–326.Google Scholar
Vallikivi, M., Hultmark, M. & Smits, A. J. 2015b Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 779, 371–389.Google Scholar
Vallikivi, M. & Smits, A. J. 2014 Fabrication and characterization of a novel nanoscale thermal anemometry probe. J. Microelectromech. Syst. 23 (4), 899–907.Google Scholar
Vincenti, P., Klewicki, J., Morrill-Winter, C., White, C. M. & Wosnik, M. 2013 Streamwise velocity statistics in turbulent boundary layers that spatially develop to high Reynolds number. Exp. Fluids 54 (12), 1–13.Google Scholar
Willert, C. E., Soria, J., Stanislas, M., Klinner, J., Amili, O., Eisfelder, M., Cuvier, C., Bellani, G., Fiorini, T. & Talamelli, A. 2017 Near-wall statistics of a turbulent pipe flow at shear Reynolds numbers up to 40 000. J. Fluid Mech. 826, R5.Google Scholar