Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T04:55:24.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Fully developed and transient concentration profiles of particulate suspensions sheared in a cylindrical Couette cell

Published online by Cambridge University Press:  15 January 2019

Mohammad Sarabian ,
Mohammadhossein Firouznia Open the ORCID record for Mohammadhossein Firouznia [Opens in a new window] ,
Bloen Metzger Open the ORCID record for Bloen Metzger [Opens in a new window]  and
Sarah Hormozi Open the ORCID record for Sarah Hormozi [Opens in a new window]
Mohammad Sarabian
Affiliation:
Department of Mechanical Engineering, Ohio University, 251 Stocker Center, Athens, OH 45701, USA
Mohammadhossein Firouznia
Affiliation:
Department of Mechanical Engineering, Ohio University, 251 Stocker Center, Athens, OH 45701, USA
Bloen Metzger
Affiliation:
Aix-Marseille Université, CNRS, IUSTI UMR 7343, 13453 Marseille, France
Sarah Hormozi*
Affiliation:
Department of Mechanical Engineering, Ohio University, 251 Stocker Center, Athens, OH 45701, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

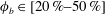We experimentally investigate particle migration in a non-Brownian suspension sheared in a Taylor–Couette configuration and in the limit of vanishing Reynolds number. Highly resolved index-matching techniques are used to measure the local particulate volume fraction. In this wide-gap Taylor–Couette configuration, we find that for a large range of bulk volume fraction, $\unicode[STIX]{x1D719}_{b}\in [20\,\%{-}50\,\%]$, the fully developed concentration profiles are well predicted by the suspension balance model of Nott & Brady (J. Fluid Mech., vol. 275, 1994, pp. 157–199). Moreover, we provide systematic measurements of the migration strain scale and of the migration amplitude which highlight the limits of the suspension balance model predictions.

JFM classification

Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 659 - 671
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbott, J. R., Tetlow, N., Graham, A. L., Altobelli, S. A., Fukushima, E., Mondy, L. A. & Stephens, T. S 1991 Experimental observations of particle migration in concentrated suspensions: Couette flow. J. Rheol. 35 (5), 773–795.Google Scholar
Alghalibi, D., Lashgari, I., Brandt, L. & Hormozi, S. 2018 Interface-resolved simulations of particle suspensions in Newtonian, shear thinning and shear thickening carrier fluids. J. Fluid Mech. 852, 329–357.Google Scholar
Boyer, F., Guazzelli, E. & Pouliquen, O. 2011 Unifying suspension and granular rheology. Phys. Rev. Lett. 107 (18), 188301.Google Scholar
Chow, A. W., Sinton, S. W., Iwamiya, J. H. & Stephens, T. S. 1994 Shear-induced particle migration in Couette and parallel-plate viscometers: NMR imaging and stress measurements. Phys. Fluids 6 (8), 2561–2576.Google Scholar
Corbett, A. M., Phillips, R. J., Kauten, R. J. & McCarthy, K. L. 1995 Magnetic resonance imaging of concentration and velocity profiles of pure fluids and solid suspensions in rotating geometries. J. Rheol. 39 (5), 907–924.Google Scholar
Dbouk, T., Lemaire, E., Lobry, L. & Moukalled, F. 2013 Shear-induced particle migration: predictions from experimental evaluation of the particle stress tensor. J. Non-Newtonian Fluid Mech. 198, 78–95.Google Scholar
Deshpande, K. V. & Shapley, N. C. 2010 Particle migration in oscillatory torsional flows of concentrated suspensions. J. Rheol. 54 (3), 663–686.Google Scholar
Duda, R. O. & Hart, P. E. 1972 Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 15 (1), 11–15.Google Scholar
Gallier, S., Lemaire, E., Lobry, L. & Peters, F. 2016 Effect of confinement in wall-bounded non-colloidal suspensions. J. Fluid Mech. 799, 100–127.Google Scholar
Gholami, M., Rashedi, A., Lenoir, N., Hautemayou, D., Ovarlez, G. & Hormozi, S. 2018 Time-resolved 2D concentration maps in flowing suspensions using X-ray. J. Rheol. 62 (4), 955–974.Google Scholar
Graham, A. L., Altobelli, S. A., Fukushima, E., Mondy, L. A. & Stephens, T. S. 1991 Note: NMR imaging of shear-induced diffusion and structure in concentrated suspensions undergoing Couette flow. J. Rheol. 35 (1), 191–201.Google Scholar
Hampton, R. E., Mammoli, A. A., Graham, A. L., Tetlow, N. & Altobelli, S. A. 1997 Migration of particles undergoing pressure-driven flow in a circular conduit. J. Rheol. 41 (3), 621–640.Google Scholar
Karnis, A., Goldsmith, H. L. & Mason, S. G. 1966 The kinetics of flowing dispersions: I. Concentrated suspensions of rigid particles. J. Colloid Interface Sci. 22 (6), 531–553.Google Scholar
Koh, C. J., Hookham, P. & Leal, L. G. 1994 An experimental investigation of concentrated suspension flows in a rectangular channel. J. Fluid Mech. 266, 1–32.Google Scholar
Leighton, D. & Acrivos, A. 1987 The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.Google Scholar
Lyon, M. K. & Leal, L. G. 1998 An experimental study of the motion of concentrated suspensions in two-dimensional channel flow. Part 1. Monodisperse systems. J. Fluid Mech. 363, 25–56.Google Scholar
Maxey, M. R. 2017 Simulation methods for particulate flows and concentrated suspensions. Annu. Rev. Fluid Mech. 49, 171–193.Google Scholar
Meek, P. C. & Norbury, J. 1982 Two-stage, two-level finite difference schemes for non-linear parabolic equations. IMA J. Numer. Anal. 2 (3), 335–356.Google Scholar
Metzger, B., Rahli, O. & Yin, X. 2013 Heat transfer across sheared suspensions: role of the shear-induced diffusion. J. Fluid Mech. 724, 527–552.Google Scholar
Morris, J. F. & Boulay, F. 1999 Curvilinear flows of noncolloidal suspensions: the role of normal stresses. J. Rheol. 43 (5), 1213–1237.Google Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven flow of suspensions: simulation and theory. J. Fluid Mech. 275, 157–199.Google Scholar
Oh, S., Song, Y. Q., Garagash, D. I., Lecampion, B. & Desroches, J. 2015 Pressure-driven suspension flow near jamming. Phys. Rev. Lett. 114 (8), 088301.Google Scholar
Ovarlez, G., Bertrand, F. & Rodts, S. 2006 Local determination of the constitutive law of a dense suspension of noncolloidal particles through magnetic resonance imaging. J. Rheol. 50 (3), 259–292.Google Scholar
Pham, P.2016 Origin of shear-induced diffusion in particulate suspensions: crucial role of solid contacts between particles. Doctoral dissertation, Aix-Marseille.Google Scholar
Phillips, R. J., Armstrong, R. C., Brown, R. A., Graham, A. L. & Abbott, J. R. 1992 A constitutive equation for concentrated suspensions that accounts for shear induced particle migration. Phys. Fluids A 4 (1), 30–40.Google Scholar
Richardson, J. & Zaki, W. 1954 Fluidization and sedimentation. Part I. Trans. Am. Inst. Chem. Engng 32, 38–58.Google Scholar
Snook, B., Butler, J. E. & Guazzelli, E. 2016 Dynamics of shear-induced migration of spherical particles in oscillatory pipe flow. J. Fluid Mech. 786, 128–153.Google Scholar
Stickel, J. J. & Powell, R. L. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149.Google Scholar