Article contents
Frontal instabilities and waves in a differentially rotating fluid
Published online by Cambridge University Press: 22 September 2011
Abstract
We present an experimental investigation of the stability of a baroclinic front in a rotating two-layer salt-stratified fluid. A front is generated by the spin-up of a differentially rotating lid at the fluid surface. In the parameter space set by rotational Froude number, 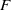 , dissipation number,
, dissipation number, 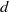 (i.e. the ratio between disk rotation time and Ekman spin-down time) and flow Rossby number, a new instability is observed that occurs for Burger numbers larger than the critical Burger number for baroclinic instability. This instability has a much smaller wavelength than the baroclinic instability, and saturates at a relatively small amplitude. The experimental results for the instability regime and the phase speed show overall a reasonable agreement with the numerical results of Gula, Zeitlin & Plougonven (J. Fluid Mech., vol. 638, 2009, pp. 27–47), suggesting that this instability is the Rossby–Kelvin instability that is due to the resonance between Rossby and Kelvin waves. Comparison with the results of Williams, Haines & Read (J. Fluid Mech., vol. 528, 2005, pp. 1–22) and Hart (Geophys. Fluid Dyn., vol. 3, 1972, pp. 181–209) for immiscible fluid layers in a small experimental configuration shows continuity in stability regimes in
(i.e. the ratio between disk rotation time and Ekman spin-down time) and flow Rossby number, a new instability is observed that occurs for Burger numbers larger than the critical Burger number for baroclinic instability. This instability has a much smaller wavelength than the baroclinic instability, and saturates at a relatively small amplitude. The experimental results for the instability regime and the phase speed show overall a reasonable agreement with the numerical results of Gula, Zeitlin & Plougonven (J. Fluid Mech., vol. 638, 2009, pp. 27–47), suggesting that this instability is the Rossby–Kelvin instability that is due to the resonance between Rossby and Kelvin waves. Comparison with the results of Williams, Haines & Read (J. Fluid Mech., vol. 528, 2005, pp. 1–22) and Hart (Geophys. Fluid Dyn., vol. 3, 1972, pp. 181–209) for immiscible fluid layers in a small experimental configuration shows continuity in stability regimes in  space, but the baroclinic instability occurs at a higher Burger number than predicted according to linear theory. Small-scale perturbations are observed in almost all regimes, either locally or globally. Their non-zero phase speed with respect to the mean flow, cusped-shaped appearance in the density field and the high values of the Richardson number for the observed wavelengths suggest that these perturbations are in many cases due to Hölmböe instability.
space, but the baroclinic instability occurs at a higher Burger number than predicted according to linear theory. Small-scale perturbations are observed in almost all regimes, either locally or globally. Their non-zero phase speed with respect to the mean flow, cusped-shaped appearance in the density field and the high values of the Richardson number for the observed wavelengths suggest that these perturbations are in many cases due to Hölmböe instability.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
Footnotes
Present address: University of Toronto, Department of Physics, Toronto, Canada
References
- 15
- Cited by


