Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T17:42:56.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Frequency lock-in mechanism in flow-induced acoustic resonance of a cylinder in a flow duct

Published online by Cambridge University Press:  17 December 2019

Zhiliang Hong Open the ORCID record for Zhiliang Hong [Opens in a new window] ,
Xiaoyu Wang ,
Xiaodong Jing Open the ORCID record for Xiaodong Jing [Opens in a new window]  and
Xiaofeng Sun Open the ORCID record for Xiaofeng Sun [Opens in a new window]
Zhiliang Hong
Affiliation:
College of Airworthiness, Civil Aviation University of China, Tianjin300300, China
Xiaoyu Wang
Affiliation:
School of Energy and Power Engineering, Beihang University, Beijing100191, China
Xiaodong Jing
Affiliation:
School of Energy and Power Engineering, Beihang University, Beijing100191, China
Xiaofeng Sun*
Affiliation:
School of Energy and Power Engineering, Beihang University, Beijing100191, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The vortex sound interaction in acoustic resonance induced by vortex shedding from a cylinder in a flow duct is numerically studied based on a nonlinear physical model, which consists of three meshless sub-models describing the vortex shedding, sound generation and propagation within the duct. In addition, the acoustic particle velocity near the separation point of the shear layer is solved and added onto the Kutta condition of the vortex shedding, which takes the acoustic feedback effect into consideration and makes the vortex sound interaction bi-directional. The predicted results of resonant frequency and amplitude are found to be in conformity with previous experiment data, especially, a continuous description of the onset–sustain–cease of lock-in phenomenon is well captured. 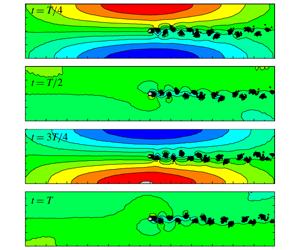The lock-in phenomenon is depicted as a vigorous competition between the vortex shedding frequency $(f_{s})$ and the inherent frequency of the acoustic $\unicode[STIX]{x1D6FD}$-mode $(f_{a})$. The mutual capturing behaviour of these two frequencies is dominated by $f_{a}$. Moreover, $f_{s}$ cannot always be locked onto $f_{a}$ within the whole lock-in region, which is in marked contrast to the previous understanding. In this aspect, two lock-in regions, the synchronous region and the $\unicode[STIX]{x1D6FD}$-mode dominant region, are defined according to the relevance of $f_{s}$ and $f_{a}$. The maximum resonant sound appears at the end of the synchronous region. The present model not only predicts the proper characteristics of frequency lock-in as observed in experiments, but also helps to provide a more detailed understanding of the underlying lock-in mechanism.

JFM classification

Acoustics: Aeroacoustics Nonlinear Dynamical Systems: Low-dimensional models Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A42
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliabadi, M. H. & Wen, P. H. 2010 Boundary Element Methods in Engineering and Sciences. Imperial College Press.CrossRefGoogle Scholar
Arafa, N. & Mohany, A. 2019 Wake structures and acoustic resonance excitation of a single finned cylinder in cross-flow. J. Fluids Struct. 86, 70–93.CrossRefGoogle Scholar
Blevins, R. D. 1984 Review of sound induced by vortex shedding from cylinders. J. Sound Vib. 92 (4), 455–470.CrossRefGoogle Scholar
Blevins, R. D. 1985 The effect of sound on vortex shedding from cylinders. J. Fluid Mech. 161, 217–237.CrossRefGoogle Scholar
Carrer, J. A. M., Pereira, W. L. A. & Mansur, W. J. 2012 Two-dimensional elastodynamics by the time-domain boundary element method: lagrange interpolation strategy in time integration. Engng Anal. Bound. Elem. 36 (7), 1164–1172.CrossRefGoogle Scholar
Crighton, D. G. 1985 The Kutta condition in unsteady flow. Annu. Rev. Fluid Mech. 17 (1), 411–445.CrossRefGoogle Scholar
Dai, X., Jing, X. & Sun, X. 2012 Discrete vortex model of a Helmholtz resonator subjected to high-intensity sound and grazing flow. J. Acoust. Soc. Am. 132 (5), 2988–2996.CrossRefGoogle ScholarPubMed
Dai, X., Jing, X. & Sun, X. 2015 Flow-excited acoustic resonance of a Helmholtz resonator: discrete vortex model compared to experiments. Phys. Fluids 27 (5), 057102.CrossRefGoogle Scholar
Dai, X. 2016 Vortex convection in the flow-excited Helmholtz resonator. J. Sound Vib. 370, 82–93.CrossRefGoogle Scholar
Ewert, R., Appel, C., Dierke, J. & Herr, M.2009 RANS/CAA based prediction of NACA0012 broadband trailing edge noise and experimental validation. AIAA 2009-3269.CrossRefGoogle Scholar
Hong, Z., Dai, X., Zhou, N., Sun, X. & Jing, X. 2014 Suppression of Helmholtz resonance using inside acoustic liner. J. Sound Vib. 333 (16), 3585–3597.CrossRefGoogle Scholar
Howe, M. S. 2003 Theory of Vortex Sound. Cambridge University Press.Google Scholar
Inoue, O. & Hatakeyama, N. 2002 Sound generation by a two-dimensional circular cylinder in a uniform flow. J. Fluid Mech. 471, 285–314.CrossRefGoogle Scholar
Jang, H. W. & Ih, J. G. 2012 Stabilization of time domain acoustic boundary element method for the interior problem with impedance boundary conditions. J. Acoust. Soc. Am. 131 (4), 2742–2752.CrossRefGoogle ScholarPubMed
Karthik, B., Chakravarthy, S. R. & Sujith, R. I. 2008 Mechanism of pipe-tone excitation by flow through an orifice in a duct. Intl J. Aeroacoust. 7, 321–347.CrossRefGoogle Scholar
Katasonov, M. M., Sung, H. J. & Bardakhanov, S. P. 2015 Wake flow-induced acoustic resonance around a long flat plate in a duct. J. Engng Thermophys-Rus 24 (1), 36–56.CrossRefGoogle Scholar
Kiya, M., Sasaki, K. & Arie, M. 1982 Discrete-vortex simulation of a turbulent separation bubble. J. Fluid Mech. 120, 219–244.CrossRefGoogle Scholar
Koch, W. 2009 Acoustic resonances and trapped modes in annular plate cascades. J. Fluid Mech. 628, 155–180.CrossRefGoogle Scholar
Liu, X., Willeke, T., Herbst, F., Yang, J. & Sume, J. 2018 A theory on the onset of acoustic resonance in a multistage compressor. Trans. ASME J. Turbomach. 140 (8), 081003.CrossRefGoogle Scholar
Langthjem, M. A. & Nakano, M. 2005 A numerical simulation of the hole-tone feedback cycle based on an axisymmetric discrete vortex method and Curle’s equation. J. Sound Vib. 288, 133–176.CrossRefGoogle Scholar
Langthjem, M. A. & Nakano, M. 2013 Application of the time-domain boundary element method to analysis of flow-acoustic interaction in a hole-tone feedback system with a tailpipe. CMES-Comput. Model. Engng 96 (4), 227–241.Google Scholar
Mills, R., Sheridan, J. & Hourigan, K. 2005 Wake of forced flow around elliptical leading edge plates. J. Fluids Struct. 20 (2), 157–176.CrossRefGoogle Scholar
Mohany, A. & Ziada, S. 2009 Numerical simulation of the flow-sound interaction mechanisms of a single and two-tandem cylinders in cross-flow. Trans. ASME J: J. Press. Vessel Technol. 131 (3), 031306.Google Scholar
Mohany, A. & Ziada, S. 2011 Measurements of the dynamic lift force acting on a circular cylinder in cross-flow and exposed to acoustic resonance. J. Fluids Struct. 27 (8), 1149–1164.CrossRefGoogle Scholar
Mohany, A. 2013 Self-excited acoustic resonance of isolated cylinders in cross-flow. AECL Nucl. Rev. 1 (1), 45–55.CrossRefGoogle Scholar
Mohany, A., Arthurs, D., Bolduc, M., Hassan, M. & Ziada, S. 2014 Numerical and experimental investigation of flow-acoustic resonance of side-by-side cylinders in a duct. J. Fluids Struct. 48, 316–331.CrossRefGoogle Scholar
Norberg, C. 2003 Fluctuating lift on a circular cylinder: review and new measurements. J. Fluids Struct. 17 (1), 57–96.CrossRefGoogle Scholar
Oberai, A., Roknaldin, F. & Hughes, T. J. R. 2002 Computation of trailing-edge noise due to turbulent flow over an airfoil. AIAA J. 40, 2206–2216.CrossRefGoogle Scholar
Parker, R. 1968 An investigation of acoustic resonance effects in an axial flow compressor stage. J. Sound Vib. 8 (2), 281–297.CrossRefGoogle Scholar
Pikovsky, A., Rosenblum, M. & Kurths, J. 2001 Synchronization: A Universal Concept in Nonlinear Science. Cambridge University Press.CrossRefGoogle Scholar
Ramos-García, N., Sarlak, H., Andersen, S. J. & Sørensen, J. N. 2017 Simulation of the flow past a circular cylinder using an unsteady panel method. Appl. Math. Model. 44, 206–222.CrossRefGoogle Scholar
Sarpkaya, T. & Schoaff, R. L. 1979 Inviscid model of two-dimensional vortex shedding by a circular cylinder. AIAA J. 17, 1193–1200.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2017 Boundary Layer Theory, 9th edn. Springer.CrossRefGoogle Scholar
Shaaban, M. & Mohany, A. 2018 Flow-induced vibration of three unevenly spaced in-line cylinders in cross-flow. J. Fluids Struct. 76, 367–383.CrossRefGoogle Scholar
Shaaban, M. & Mohany, A. 2019 Phase-resolved PIV measurements of flow over three unevenly spaced cylinders and its coupling with acoustic resonance. Exp. Fluids 60, 71.CrossRefGoogle Scholar
Seo, J. H. & Moon, Y. J. 2007 Aerodynamic noise prediction for long-span bodies. J. Sound Vib. 306, 564–579.CrossRefGoogle Scholar
Tan, B. T., Thompson, M. C. & Hourigan, K. 2004 Flow past rectangular cylinders: receptivity to transverse forcing. J. Fluid Mech. 515, 33–62.CrossRefGoogle Scholar
Wu, L., Jing, X. & Sun, X. 2017 Prediction of vortex-shedding noise from the blunt trailing edge of a flat plate. J. Sound Vib. 408, 20–30.CrossRefGoogle Scholar
Yokoyama, H., Kitamiya, K. & Iida, A. 2013 Flows around a cascade of flat plates with acoustic resonance. Phys. Fluids 25 (10), 106104.CrossRefGoogle Scholar
Zhang, W., Li, X., Ye, Z. & Jiang, Y. 2015 Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers. J. Fluid Mech. 783, 72–102.CrossRefGoogle Scholar
Ziada, S. & Lafon, P. 2013 Flow-excited acoustic resonance excitation mechanism, design guidelines, and counter measures. Appl. Mech. Rev. 66, 010802.Google Scholar