Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T16:28:13.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Free-surface gravity currents propagating in an open channel containing a porous layer at the free surface

Published online by Cambridge University Press:  15 November 2016

Ayse Yuksel-Ozan ,
George Constantinescu  and
Heidi Nepf
Ayse Yuksel-Ozan
Affiliation:
Department of Civil and Environmental Engineering & IIHR-Hydroscience and Engineering, The University of Iowa, Iowa City, IA 52242, USA Department of Civil Engineering, Adnan Menderes University, Main Campus, 09100, Aydin, Turkey
George Constantinescu*
Affiliation:
Department of Civil and Environmental Engineering & IIHR-Hydroscience and Engineering, The University of Iowa, Iowa City, IA 52242, USA
Heidi Nepf
Affiliation:
Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Large eddy simulation (LES) is used to study the evolution and structure of a lock-exchange, Boussinesq gravity current forming in a channel partially blocked by a porous layer. This configuration is used to understand how the characteristics of a surface layer containing floating vegetation affects the generation of thermally driven convective water exchange in a long shallow channel. The porous layer, which represents the roots of the floating vegetation, contains a staggered array of rigid square cylinders of edge length 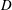$D$ with solid volume fraction 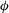$\unicode[STIX]{x1D719}$. The cylinders extend over a depth 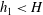$h_{1}<H$ below the free surface, where 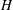$H$ is the channel depth. The surface current of lighter fluid splits into two layers, one propagating slowly inside the porous layer and the other flowing beneath the porous layer. The main geometrical parameters of the porous layer, 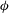$\unicode[STIX]{x1D719}$ and 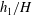$h_{1}/H$, have a large effect on the dynamics and structure of the surface current and the temporal variation of the front position. For cases with sufficiently large values of 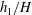$h_{1}/H$ and 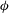$\unicode[STIX]{x1D719}$, the front within the porous layer approaches the triangular shape observed for low Reynolds number lock-exchange currents propagating in a channel containing cylinders over its whole volume (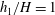$h_{1}/H=1$), and the surface current transitions to a drag-dominated regime in which the front velocity is proportional to 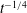$t^{-1/4}$, where $t$ is the time since the current is initiated. For sufficiently high values of 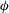$\unicode[STIX]{x1D719}$, the velocity of the fluid inside the porous layer is close to zero at all locations except for those situated close to the lock gate and for some distance behind the front. Close to the front, lighter fluid from below penetrates into the porous layer due to unstable stratification at the bottom of the porous layer. Simulation results are also used to assess how $\unicode[STIX]{x1D719},h_{1}/H$ and the Reynolds number affect the rate at which the heavier fluid situated initially inside the porous layer is removed by the advancing surface current and the main mixing mechanisms. Based on the estimated time scales for flushing the porous (root) layer, we show that flushing can significantly enhance the overall rate of nutrient removal by the floating vegetation by maintaining a higher concentration of nutrients within the root layer.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents
Type
Papers
Information
Journal of Fluid Mechanics , Volume 809 , 25 December 2016 , pp. 601 - 627
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, C. S., Boar, R., Hubble, D. S., Gikundgu, M., Harper, D. M., Hickley, P. & Tarras-Wahlberg, N. 2002 The dynamics and ecology of exotic tropical species in floating plant mats: Lake Naivasha, Kenya. Hydrobiologia 488, 115–122.Google Scholar
Andradottir, A. & Nepf, H. 2001 Impact of exchange flows on wetland flushing. Water Resour. Res. 37 (12), 3265–3274.Google Scholar
Azza, N., Denny, P., van de Koppel, J. & Kansiime, F. 2006 Floating mats: their occurrence and influence on shoreline distribution of emergent vegetation. Freshwat. Biol. 51 (7), 1286–1297.CrossRefGoogle Scholar
Chang, K. S., Constantinescu, G. & Park, S. O. 2006 Analysis of the flow and mass transfer processes for the incompressible flow past an open cavity with a laminar and a fully turbulent incoming boundary layer. J. Fluid Mech. 561, 113–145.CrossRefGoogle Scholar
Chang, K., Constantinescu, G. & Park, S. O. 2007 The purging of a neutrally buoyant or a dense miscible contaminant from a rectangular cavity. Part II: the case of an incoming fully turbulent overflow. ASCE J. Hydraul. Engng 133 (4), 373–385.CrossRefGoogle Scholar
Chang, K. S. & Constantinescu, G. 2015 Numerical investigation of flow and turbulence structure through and around a circular array of rigid cylinders. J. Fluid Mech. 776, 161–199.CrossRefGoogle Scholar
Chimney, M. J., Wenkert, L. & Pietro, K. C. 2006 Patterns of vertical stratification in a subtropical constructed wetland in south Florida (USA). Ecol. Engng 27, 322–330.CrossRefGoogle Scholar
Coates, M. & Paterson, J. C. 1993 Unsteady natural convection in a cavity with non-uniform absorption of radiation. J. Fluid Mech. 256, 133–161.CrossRefGoogle Scholar
Constantinescu, G. 2014 LES of lock-exchange compositional gravity currents: a brief review of some recent results. Environ. Fluid Mech. 14, 295–317.CrossRefGoogle Scholar
Downing-Kunz, M. A. & Stacey, M. 2012 Observations of mean and turbulent flow structure in a free floating macrophyte root canopy. Limnol. Oceanogr. 2 (1), 67–79.Google Scholar
Edwards, A. M., Wright, D. G. & Platt, T. 2004 Biological heating effects of a band of phytoplankton. J. Mar. Syst. 49, 89–103.Google Scholar
Gonzalez-Juez, E., Meiburg, E., Tokyay, T. & Constantinescu, G. 2010 Gravity current flow past a circular cylinder: forces and wall shear stresses and implications for scour. J. Fluid Mech. 649, 69–102.CrossRefGoogle Scholar
Hartel, C., Meiburg, E. & Necker, F. 2000 Analysis and direct numerical simulation of the flow at a gravity-current head. Part 1. Flow topology and front speed for slip and no-slip boundaries. J. Fluid Mech. 418, 189–212.Google Scholar
Hatcher, L., Hogg, A. J. & Woods, A. W. 2000 The effects of drag on turbulent gravity currents. J. Fluid Mech. 416, 297–314.Google Scholar
Hill, R., Webb, G. & Smith, A. 1987 Floating vegetation mats on a floodplain billalong in the Northern Territory of Australia. Hydrobiologia 150, 153–164.Google Scholar
Imaoka, T. & Teranishi, S. 1988 Rates of nutrient uptake and growth of the water hyacinth [Eichhornia Crassipes (MART.) Solms]. Water Resour. Res. 22 (8), 943–951.Google Scholar
Jamali, M., Zhang, X. & Nepf, H. 2008 Exchange flow between a canopy and open water. J. Fluid Mech. 611, 237–254.CrossRefGoogle Scholar
James, W. F. & Barko, J. W. 1991 Estimation of phosphorus exchange between littoral and pelagic zones during nighttime convection circulation. Limnol. Oceanogr. 36 (1), 179–187.CrossRefGoogle Scholar
James, W. F., Barko, J. W. & Eakin, H. L. 1994 Convective water exchanges during differential cooling and heating: implications for dissolved constituent transport. Hydrobiologia 394, 167–176.Google Scholar
King, A. T., Tinoco, R. O. & Cowen, E. A. 2012 A 𝜅–𝜀 turbulence model based on the scales of vertical shear and stem wakes valid for emergent and submerged vegetated flows. J. Fluid Mech. 701, 1–39.CrossRefGoogle Scholar
Lightbody, A., Avener, M. & Nepf, H. 2008 Observations of short- circuiting flow paths within a free-surface wetland in Augusta, Georgia, USA. Limnol. Oceanogr. 53 (3), 1040–1053.Google Scholar
Lovstedt, C. & Bengtsson, L. 2008 Density-driven current between reed belts and open water of a shallow lake. Water Resour. Res. 44, W10413.CrossRefGoogle Scholar
Necker, F., Härtel, C., Kleiser, L. & Meiburg, E. 2005 Mixing and dissipation in particle-drive gravity currents. J. Fluid Mech. 545, 339–372.Google Scholar
Ooi, S. K., Constantinescu, G. & Weber, L. J. 2007a 2D Large Eddy Simulation of lock-exchange gravity current flows. ASCE J. Hydraul. Engng 133 (4), 361–372.Google Scholar
Ooi, S. K., Constantinescu, S. G. & Weber, L. 2007b A numerical study of intrusive compositional gravity currents. Phys. Fluids 19, 076602.Google Scholar
Ooi, S. K., Constantinescu, S. G. & Weber, L. 2009 Numerical simulations of lock exchange compositional gravity currents. J. Fluid Mech. 635, 361–388.Google Scholar
Ozan, A. Y., Constantinescu, G. & Hogg, A. J. 2015 Lock-exchange gravity currents propagating in a channel containing an array of obstacles. J. Fluid Mech. 765, 544–575.Google Scholar
Padial, A. A., Thomas, S. M. & Agostinho, A. 2009 Effects of structural heterogeneity provided by the floating macrophyte Eichhornia azurea on the predation efficiency and habitat use of the small Neotropical fish Moenkhausia sanctaefilomenae. Hydrobiologia 624, 161–170.Google Scholar
Pierce, C. D. & Moin, P.2001 Progress-variable approach for large-eddy simulation of turbulent combustion. Mech. Eng. Dept. Rep. TF-80, Stanford University, California, USA.Google Scholar
Pierce, C. D. & Moin, P. 2004 Progress-variable approach for large-eddy simulation of nonpremixed turbulent combustion. J. Fluid Mech. 504, 73–97.Google Scholar
Rodi, W., Constantinescu, G. & Stoesser, T. 2013 Large Eddy Simulation in Hydraulics. CRC Press, Taylor & Francis Group.Google Scholar
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.Google Scholar
Tanino, Y., Nepf, H. M. & Kulis, P. S. 2005 Gravity currents in aquatic canopies. Water Resour. Res. 41, W12402.CrossRefGoogle Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2011 Lock exchange gravity currents with a high volume of release propagating over an array of obstacles. J. Fluid Mech. 672, 570–605.CrossRefGoogle Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2012 Tail structure and bed friction velocity distribution of gravity currents propagating over an array of obstacles. J. Fluid Mech. 694, 252–291.Google Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2014 Lock exchange gravity currents with a low volume of release propagating over an array of obstacles. J. Geophys. Res. Ocean 119, 2752–2768.Google Scholar
Tokyay, T. & Constantinescu, G. 2015 The effects of a submerged non-erodible triangular obstacle on bottom propagating gravity currents. Phys. Fluids 27 (5), 056601.CrossRefGoogle Scholar
Ultsch, G. 1973 The effect of water hyacinth (Eichhornia crassipes) on the microenvironment of aquatic communities. Arch. Hydrobiol. 72, 460–473.Google Scholar
Wang, C. Y. & Sample, D. J. 2014 Assessment of the nutrient removal effectiveness of floating treatment wetlands applied to urban retention ponds. J. Environ. Manage. 137, 23–35.Google Scholar
Zhang, X. & Nepf, H. 2008 Density-driven exchange flow between open water and an aquatic canopy. Water Resour. Res. 44, W08417.Google Scholar
Zhang, X. & Nepf, H. 2011 Exchange flow between open water and floating vegetation. Environ. Fluid Mech. doi:10.1007/s10652-011-9213-4.Google Scholar

Yuksel-Ozan Movie 1

Effect of solid volume fraction. Current is visualized based on nondimensional density (top three frames φ=8%, 16% and 24%) and spanwise vorticity fields (next three frames). Bottom two frames shows a zoom of the concentration field.

Download Yuksel-Ozan Movie 1(Video)
Video 5.2 MB

Yuksel-Ozan Movie 2

Effect of depth of porous layer. Current is visualized based on nondimensional density (top three frames corresponding to a relative height of the porous layer h1/H=0.1, 0.27 and 0.5) and spanwise vorticity (next three frames) fields. The bottom frames show a detailed view of the concentration field

Download Yuksel-Ozan Movie 2(Video)
Video 6.6 MB

Yuksel-Ozan Movie 3

Effect of Reynolds number. Current is visualized based on nondimensional density (top two frames showing Re=5,700 and Re=500,000 cases) and spanwise vorticity fields (next two frames). The bottom 4 frames show a detailed view of the concentration and vorticity fields.

Download Yuksel-Ozan Movie 3(Video)
Video 4.3 MB