Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T11:27:18.187Z Has data issue: false hasContentIssue false
  • English
  • Français

A free flexible flap in channel flow

Published online by Cambridge University Press:  25 April 2022

Chang Xu Open the ORCID record for Chang Xu [Opens in a new window] ,
Xuechao Liu ,
Kui Liu Open the ORCID record for Kui Liu [Opens in a new window] ,
Yongfeng Xiong  and
Haibo Huang Open the ORCID record for Haibo Huang [Opens in a new window]
Chang Xu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Xuechao Liu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Kui Liu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Yongfeng Xiong
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Haibo Huang*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

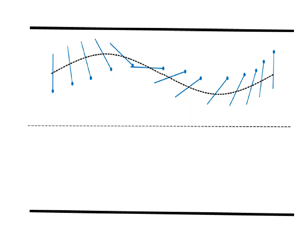
Fine fibre immersed in different flows is ubiquitous. For a fibre in shear flows, most motion modes appear in the flow-gradient plane. Here the two-dimensional behaviours of an individual flexible flap in channel flows are studied. The nonlinear coupling of the fluid inertia ($\textit {Re}$), flexibility of the flap ($K$) and channel width ($W$) is discovered. Inside a wide channel (e.g. $W=4$), as $K$ decreases, the flap adopts rigid motion, springy motion, snake turn and complex mode in sequence. It is found that the fluid inertia tends to straighten the flap. Moreover, $\textit {Re}$ significantly affects the lateral equilibrium location $y_{eq}$, therefore affecting the local shear rate and the tumbling period $T$. For a rigid flap in a wide channel, when $\textit {Re}$ exceeds a threshold, the flap stays inclined instead of tumbling. As $\textit {Re}$ further increases, the flap adopts swinging mode. In addition, there is a scaling law between $T$ and $\textit {Re}$. For the effect of $K$, through the analysis of the torque generated by surrounding fluid, we found that a smaller $K$ slows down the tumbling of the flap even if $y_{eq}$ is comparable. As $W$ decreases, the wall confinement effect makes the flap easier to deform and closer to the centreline. The tumbling period would increase and the swinging mode would be more common. When $W$ further decreases, the flaps are constrained to stay inclined, parabolic-like or one-end bending configurations moving along with the flow. Our study may shed some light on the behaviours of a free fibre in flows.

JFM classification

Aerodynamics: Flow-structure interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 941 , 25 June 2022 , A12
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aidun, C.K., Lu, Y. & Ding, E.-J. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.CrossRefGoogle Scholar
Banaei, A.A., Rosti, M.E. & Brandt, L. 2020 Numerical study of filament suspensions at finite inertia. J. Fluid Mech. 882, A5.CrossRefGoogle Scholar
Becker, L.E. & Shelley, M.J. 2001 Instability of elastic filaments in shear flow yields first-normal-stress differences. Phys. Rev. Lett. 87 (19), 198301.CrossRefGoogle ScholarPubMed
Bretherton, F.P. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14, 284–304.CrossRefGoogle Scholar
Chelakkot, R., Winkler, R.G. & Gompper, G. 2010 Migration of semiflexible polymers in microcapillary flow. Europhys. Lett. 91, 14001.CrossRefGoogle Scholar
Chen, S. & Doolen, G.D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30 (1), 329–364.CrossRefGoogle Scholar
Chen, S.-D., Pan, T.-W. & Chang, C.-C. 2012 The motion of a single and multiple neutrally buoyant elliptical cylinders in plane Poiseuille flow. Phys. Fluids 24 (10), 103302.CrossRefGoogle Scholar
Cox, R.G. 1971 The motion of long slender bodies in a viscous fluid. Part 2. Shear flow. J. Fluid Mech. 45, 625–657.CrossRefGoogle Scholar
Ding, E. & Aidun, C.K. 2000 The dynamics and scaling law for particles suspended in shear flow with inertia. J. Fluid Mech. 423, 317–344.CrossRefGoogle Scholar
Doyle, J.F. 2013 Nonlinear Analysis of Thin-Walled Structures: Statics, Dynamics, and Stability. Springer.Google Scholar
Du Roure, O., Lindner, A., Nazockdast, E.N. & Shelley, M.J. 2019 Dynamics of flexible fibers in viscous flows and fluids. Annu. Rev. Fluid Mech. 51, 539–572.CrossRefGoogle Scholar
Eldredge, J. 2007 Numerical simulation of the fluid dynamics of 2D rigid body motion with the vortex particle method. J. Comput. Phys. 221 (2), 626–648.CrossRefGoogle Scholar
Farutin, A., Piasecki, T., Słowicka, A.M., Misbah, C., Wajnryb, E. & Ekiel-Jeżewska, M.L. 2016 Dynamics of flexible fibers and vesicles in Poiseuille flow at low Reynolds number. Soft Matt. 12 (35), 7307–7323.CrossRefGoogle ScholarPubMed
Fauci, L.J. & Dillon, R. 2006 Biofluidmechanics of reproduction. Annu. Rev. Fluid Mech. 38, 371–394.CrossRefGoogle Scholar
Favier, J., Li, C., Kamps, L., Revell, A., O'Connor, J. & Brücker, C. 2017 The PELskin project–Part I: fluid–structure interaction for a row of flexible flaps: a reference study in oscillating channel flow. Meccanica 52 (8), 1767–1780.CrossRefGoogle Scholar
Forgacs, O.L. & Mason, S.G. 1959 Particle motions in sheared suspensions: X. Orbits of flexible threadlike particles. J. Colloid Sci. 14 (5), 473–491.CrossRefGoogle Scholar
Goldstein, D., Handler, R. & Sirovich, L. 1993 Modeling a no-slip flow boundary with an external force field. J. Comput. Phys. 105 (2), 354–366.CrossRefGoogle Scholar
Guo, Z., Zheng, C. & Shi, B. 2002 Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 65, 046308.CrossRefGoogle ScholarPubMed
Harasim, M., Wunderlich, B., Peleg, O., Kröger, M. & Bausch, A.R. 2013 Direct observation of the dynamics of semiflexible polymers in shear flow. Phys. Rev. Lett. 110 (10), 108302.CrossRefGoogle ScholarPubMed
Hinch, E.J. 1976 The distortion of a flexible inextensible thread in a shearing flow. J. Fluid Mech. 74 (2), 317–333.CrossRefGoogle Scholar
Huang, H., Wei, H. & Lu, X.-Y. 2018 Coupling performance of tandem flexible inverted flags in a uniform flow. J. Fluid Mech. 837, 461–476.CrossRefGoogle Scholar
Huang, W.-X., Chang, C.B. & Sung, H.J. 2011 An improved penalty immersed boundary method for fluid–flexible body interaction. J. Comput. Phys. 230, 5061–5079.CrossRefGoogle Scholar
Jeffery, G.B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102 (715), 161–179.Google Scholar
Karnis, A., Goldsmith, H.L. & Mason, S.G. 1966 The flow of suspensions through tubes: V. Inertial effects. Can. J. Chem. Engng 44 (4), 181–193.CrossRefGoogle Scholar
Kuei, S., Słowicka, A.M., Ekiel-Jeżewska, M.L., Wajnryb, E. & Stone, H.A. 2015 Dynamics and topology of a flexible chain: knots in steady shear flow. New J. Phys. 17 (5), 053009.CrossRefGoogle Scholar
LaGrone, J., Cortez, R., Yan, W. & Fauci, L. 2019 Complex dynamics of long, flexible fibers in shear. J. Non-Newtonian Fluid Mech. 269, 73–81.CrossRefGoogle Scholar
Lindner, A. & Shelley, M. 2015 Elastic fibers in flows. In Fluid-Structure Interactions in Low-Reynolds-Number Flows (ed. C. Duprat & H.A. Stone), pp. 168–189. Royal Society of Chemistry.CrossRefGoogle Scholar
Lindström, S.B. & Uesaka, T. 2007 Simulation of the motion of flexible fibers in viscous fluid flow. Phys. Fluids 19, 113307.CrossRefGoogle Scholar
Liu, Y., Chakrabarti, B., Saintillan, D., Lindner, A. & Du Roure, O. 2018 Morphological transitions of elastic filaments in shear flow. Proc. Natl Acad. Sci. USA 115 (38), 9438–9443.CrossRefGoogle ScholarPubMed
Lundell, F., Söderberg, L.D. & Alfredsson, P.H. 2011 Fluid mechanics of papermaking. Annu. Rev. Fluid Mech. 43, 195–217.CrossRefGoogle Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261.CrossRefGoogle Scholar
Nagel, M., Brun, P.-T., Berthet, H., Lindner, A., Gallaire, F. & Duprat, C. 2018 Oscillations of confined fibres transported in microchannels. J. Fluid Mech. 835, 444–470.CrossRefGoogle Scholar
Nepf, H. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.CrossRefGoogle Scholar
Nguyen, H. & Fauci, L. 2014 Hydrodynamics of diatom chains and semiflexible fibres. J. R. Soc. Interface 11 (96), 20140314.CrossRefGoogle ScholarPubMed
O'Connor, J. & Revell, A. 2019 Dynamic interactions of multiple wall-mounted flexible flaps. J. Fluid Mech. 870, 189–216.CrossRefGoogle Scholar
Peng, Z.-R., Huang, H. & Lu, X.-Y. 2018 Hydrodynamic schooling of multiple self-propelled flapping plates. J. Fluid Mech. 853, 587–600.CrossRefGoogle Scholar
Peskin, C.S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.CrossRefGoogle Scholar
Reddig, S. & Stark, H. 2011 Cross-streamline migration of a semiflexible polymer in a pressure driven flow. J. Chem. Phys. 135, 165101.CrossRefGoogle Scholar
Sierou, A. & Brady, J.F. 2004 Shear-induced self-diffusion in non-colloidal suspensions. J. Fluid mech. 506, 285–314.CrossRefGoogle Scholar
Skjetne, P., Ross, R.F. & Klingenberg, D.J. 1997 Simulation of single fiber dynamics. J. Chem. Phys. 107 (6), 2108–2121.CrossRefGoogle Scholar
Słowicka, A.M., Ekiel-Jeżewska, M.L., Sadlej, K. & Wajnryb, E. 2012 Dynamics of fibers in a wide microchannel. J. Chem. Phys. 136 (4), 044904.CrossRefGoogle Scholar
Słowicka, A.M., Stone, H.A. & Ekiel-Jeżewska, M.L. 2020 Flexible fibers in shear flow approach attracting periodic solutions. Phys. Rev. E 101 (2), 023104.CrossRefGoogle ScholarPubMed
Słowicka, A.M., Wajnryb, E. & Ekiel-Jeżewska, M.L. 2013 Lateral migration of flexible fibers in Poiseuille flow between two parallel planar solid walls. Eur. Phys. J. E 36 (3), 31.CrossRefGoogle ScholarPubMed
Smith, D.E., Babcock, H.P. & Chu, S. 1999 Single-polymer dynamics in steady shear flow. Science 283 (5408), 1724–1727.CrossRefGoogle ScholarPubMed
Steinhauser, D., Köster, S. & Pfohl, T. 2012 Mobility gradient induces cross-streamline migration of semiflexible polymers. ACS Macro Lett. 1, 541–545.CrossRefGoogle Scholar
Subramanian, G. & Koch, D.L. 2005 Inertial effects on fibre motion in simple shear flow. J. Fluid Mech. 535, 383–414.CrossRefGoogle Scholar
Thiébaud, M., Shen, Z., Harting, J. & Misbah, C. 2014 Prediction of anomalous blood viscosity in confined shear flow. Phys. Rev. Lett. 112 (23), 238304.CrossRefGoogle ScholarPubMed
Trevelyan, B.J. & Mason, S.G. 1951 Particle motions in sheared suspensions. I. Rotations. J. Colloid Sci. 6 (4), 354–367.CrossRefGoogle Scholar
Wang, Z., Birch, J. & Dickinson, M. 2004 Unsteady forces and flows in low Reynolds number hovering flight: two-dimensional computations vs robotic wing experiments. J. Expl Biol. 207 (3), 449–460.CrossRefGoogle ScholarPubMed
Wu, J. & Aidun, C.K. 2010 A method for direct simulation of flexible fiber suspensions using lattice Boltzmann equation with external boundary force. Intl J. Multiphase Flow 36, 202–209.CrossRefGoogle Scholar
Yin, B. & Luo, H. 2010 Effect of wing inertia on hovering performance of flexible flapping wings. Phys. Fluids 22 (11), 111902.CrossRefGoogle Scholar
Zhang, C., Huang, H. & Lu, X.-Y. 2020 Effect of trailing-edge shape on the self-propulsive performance of heaving flexible plates. J. Fluid Mech. 887, A7.CrossRefGoogle Scholar