Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Peters, Ivo R.
Madonia, Matteo
Lohse, Detlef
and
van der Meer, Devaraj
2016.
Volume entrained in the wake of a disk intruding into an oil-water interface.
Physical Review Fluids,
Vol. 1,
Issue. 3,
Piumsuwan, T
Seesomboon, E
and
Pussadee, N
2018.
Investigation of Half-Ring Vortices Generated by Half-Submerged Thin Circular Plate Using Digital Particle Image Velocimetry Method.
Journal of Physics: Conference Series,
Vol. 1144,
Issue. ,
p.
012172.
Qin, Suyang
Liu, Hong
and
Xiang, Yang
2018.
On the formation modes in vortex interaction for multiple co-axial co-rotating vortex rings.
Physics of Fluids,
Vol. 30,
Issue. 1,
David, M. Jimreeves
Mathur, Manikandan
Govardhan, R. N.
and
Arakeri, J. H.
2018.
The kinematic genesis of vortex formation due to finite rotation of a plate in still fluid.
Journal of Fluid Mechanics,
Vol. 839,
Issue. ,
p.
489.
Yu, W.
Ferreira, C.
and
van Kuik, G.A.M.
2019.
The dynamic wake of an actuator disc undergoing transient load: A numerical and experimental study.
Renewable Energy,
Vol. 132,
Issue. ,
p.
1402.
Xing, Boyang
Li, Dongdong
Zhang, Bin
Xu, Hui
and
Liu, Hong
2021.
Vortex structures evolution in supersonic mixing layers with different inlet Reynolds numbers based on the Lagrangian method.
AIP Advances,
Vol. 11,
Issue. 12,
Lin, Shujia
Wang, Fuxin
Li, Zhuoqi
and
Xiang, Yang
2021.
Proceedings of the International Conference on Aerospace System Science and Engineering 2020.
Vol. 680,
Issue. ,
p.
153.
Xiang, Yang
Li, Zhuoqi
Qin, Suyang
and
Liu, Hong
2021.
Formation number and pinch-off signals of disc vortex ring based on a Lagrangian analysis.
Experimental Thermal and Fluid Science,
Vol. 129,
Issue. ,
p.
110452.
de Guyon, Guillaume
and
Mulleners, Karen
2021.
Scaling of the translational velocity of vortex rings behind conical objects.
Physical Review Fluids,
Vol. 6,
Issue. 2,
Wu, Xiaoyu
Wu, Hengtian
Zhang, Ning
and
Dai, Hongcai
2022.
A Comprehensive Evaluation Method of Integrated Energy System based on Hierarchical Decomposition.
p.
290.
Li, Zhuoqi
Xiang, Yang
Qin, Suyang
Liu, Hong
and
Wang, Fuxin
2022.
Two models and the generation mechanisms of the drag on an accelerating starting disk.
Physics of Fluids,
Vol. 34,
Issue. 8,
de Guyon, Guillaume
and
Mulleners, Karen
2022.
Estimating the non-dimensional energy of vortex rings by modelling their roll-up.
Journal of Fluid Mechanics,
Vol. 940,
Issue. ,
Steiner, Joanne
Morize, Cyprien
Delbende, Ivan
Sauret, Alban
and
Gondret, Philippe
2023.
Vortex rings generated by a translating disk from start to stop.
Physical Review Fluids,
Vol. 8,
Issue. 6,
Li, Zhuoqi
Chen, Lunbing
Xiang, Yang
Liu, Hong
and
Wang, Fuxin
2024.
Two independent mechanisms with distinct laws for the generation of drag force on accelerating plates.
Physics of Fluids,
Vol. 36,
Issue. 10,
Chao, Li-Ming
Couzin, Iain D.
and
Li, Liang
2024.
On turning maneuverability in self-propelled burst-and-coast swimming.
Physics of Fluids,
Vol. 36,
Issue. 11,
Chao, Li-Ming
Jia, Laibing
Wang, Siyuan
Liberzon, Alexander
Ravi, Sridhar
Couzin, Iain D
Li, Liang
and
Grest, Gary
2024.
Tailbeat perturbations improve swimming efficiency by reducing the phase lag between body motion and the resulting fluid response.
PNAS Nexus,
Vol. 3,
Issue. 3,
Zhu, Jianwei
Zhang, Guoqing
Yu, S.C.M.
Gao, Lei
and
Zhao, Ruijia
2024.
Formation and development of the stopping vortex ring in starting jets.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Turkevich, Leonid A.
Chen, Hongyu
and
Jog, Milind A.
2025.
Dust resuspension from the splash of a falling powder: A numerical aerodynamic simulation of a pellet falling onto a powder monolayer.
Aerosol Science and Technology,
Vol. 59,
Issue. 1,
p.
49.
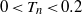 $0\lt {T}_{n} \lt 0. 2$) during which Taylor’s inviscid estimation is valid, the circulation of the vortex ring grows and the translational velocity of the vortex ring decreases. In the stable growth phase (
$0\lt {T}_{n} \lt 0. 2$) during which Taylor’s inviscid estimation is valid, the circulation of the vortex ring grows and the translational velocity of the vortex ring decreases. In the stable growth phase (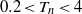 $0. 2\lt {T}_{n} \lt 4$), the growth rate of the circulation decreases gradually. In the non-axisymmetric phase (
$0. 2\lt {T}_{n} \lt 4$), the growth rate of the circulation decreases gradually. In the non-axisymmetric phase (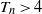 ${T}_{n} \gt 4$), the ring loses axisymmetry due to instability. Compared with the vortex ring generated by the laminar flow from an orifice, the one generated by a circular disc always moves with the disc, and the entrained fluid decreases and the saturated circulation increases. The temporal impulse exerted by the moving disc on the fluid is estimated by DPIV measurements and is calculated using the direct momentum conservation method. The momentum of the control volume enclosing the LCS is found to occupy 64–68 % of the entire impulse exerted by the disc on the fluid.
${T}_{n} \gt 4$), the ring loses axisymmetry due to instability. Compared with the vortex ring generated by the laminar flow from an orifice, the one generated by a circular disc always moves with the disc, and the entrained fluid decreases and the saturated circulation increases. The temporal impulse exerted by the moving disc on the fluid is estimated by DPIV measurements and is calculated using the direct momentum conservation method. The momentum of the control volume enclosing the LCS is found to occupy 64–68 % of the entire impulse exerted by the disc on the fluid.

