Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T13:49:20.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Formation of particle clouds

Published online by Cambridge University Press:  31 March 2014

B. Zhao ,
A. W. K. Law ,
E. E. Adams  and
J. W. Er
B. Zhao
Affiliation:
School of Civil and Environmental Engineering, Nanyang Technological University, 50 Nanyang Avenue, 639798, Republic of Singapore DHI-NTU Centre, Nanyang Environment and Water Research Institute, Nanyang Technological University, 1 Cleantech Loop, 637141, Republic of Singapore
A. W. K. Law*
Affiliation:
School of Civil and Environmental Engineering, Nanyang Technological University, 50 Nanyang Avenue, 639798, Republic of Singapore DHI-NTU Centre, Nanyang Environment and Water Research Institute, Nanyang Technological University, 1 Cleantech Loop, 637141, Republic of Singapore
E. E. Adams
Affiliation:
Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
J. W. Er
Affiliation:
School of Civil and Environmental Engineering, Nanyang Technological University, 50 Nanyang Avenue, 639798, Republic of Singapore
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the literature, it has been conceptualized that a group of dense particles released instantaneously into homogeneous stagnant water would form a circulating vortex cloud and descend through the water column as a thermal. However, Wen & Nacamuli (Hydrodynamics: Theory and Applications, 1996, pp. 1275–1280) observed the formation of particle clumps characterized by a narrow, fast-moving core shedding particles into the wake. They found clump formation to be possible even for particles in the non-cohesive range as long as the source Rayleigh number was large ($\mathit{Ra} > {10^3}$) or, equivalently, the source cloud number was small (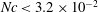$\mathit{Nc} < 3.2 \times 10^{-2}$). This physical phenomenon has not been investigated further since the experiments of Wen and Nacamuli. In the present study, the relationship between Nc and the formation process is examined more systematically. The theoretical support for cloud number dependence is explored by considering flows passing a porous sphere. Here 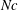$\mathit{Nc}$ values ranging from 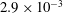$2.9 \times 10^{-3}$ to 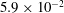$5.9 \times 10^{-2}$ are tested experimentally using particles with different initial masses and grain sizes, from non-cohesive to marginally cohesive. The formation processes are categorized into cloud formation, a transitional regime and clump formation, and their distinct features are presented through qualitative description of the flow patterns and quantitative assessment of the gross characteristics.

JFM classification

Convection: Convection Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 746 , 10 May 2014 , pp. 193 - 213
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bühler, J. & Papantoniou, D. A. 2001 On the motion of suspension thermals and particle swarms. J. Hydraul. Res. 39 (6), 643–653.CrossRefGoogle Scholar
Burridge, H. C. & Hunt, G. R. 2012 The rise heights of low- and high-Froude-number turbulent axisymmetric fountains. J. Fluid Mech. 691, 392–416.Google Scholar
Bush, J. W. M., Thurber, B. A. & Blanchette, F. 2003 Particle clouds in homogeneous and stratified environments. J. Fluid Mech. 489, 29–54.Google Scholar
Cheng, N. S. 2003 Application of Ergun equation to computation of critical shear velocity subject to seepage. J. Irrig. Drain. Engng ASCE 129 (4), 278–283.Google Scholar
Deguen, R., Olson, P. & Cardin, P. 2011 Experiments on turbulent metal-silicate mixing in a magma ocean. Earth Planet. Sci. Lett. 310 (3–4), 303–313.CrossRefGoogle Scholar
Dietrich, W. E. 1982 Settling velocity of natural particles. Water Resour. Res. 18 (6), 1615–1626.CrossRefGoogle Scholar
Ergun, S. 1952 Fluid flow through packed columns. Chem. Engng Prog. 48, 89–94.Google Scholar
Gensheimer, R. J., Adams, E. E. & Law, A. W. K. 2013 Dynamics of particle clouds in ambient currents with application to open-water sediment disposal. J. Hydraul. Engng 139 (2), 114–123.CrossRefGoogle Scholar
Gu, J. & Li, C. W. 2004 Modelling instantaneous discharge of unsorted particle cloud in ambient water by an Eulerian–Lagrangian method. J. Hydraul. Res. 42 (4), 399–405.Google Scholar
Lai, A. C. H., Zhao, B., Law, A. W. K. & Adams, E. E. 2013 Two-phase modelling of sediment clouds. Environ. Fluid Mech. 13, 435–463.CrossRefGoogle Scholar
Lamb, H. 1993 Hydrodynamics. Cambridge University Press.Google Scholar
Li, C. W. 1997 Convection of particle thermals. J. Hydraul. Res. 35 (3), 363–376.Google Scholar
Lundgren, T. S., Yao, J. & Mansour, N. N. 1992 Microburst modelling and scaling. J. Fluid Mech. 239, 461–488.CrossRefGoogle Scholar
Niven, R. K. 2002 Physical insight into the Ergun and Wen & Yu equations for fluid flow in packed and fluidised beds. Chem. Engng Sci. 57, 527–534.CrossRefGoogle Scholar
Rahimipour, H. & Wilkinson, D. 1992 Dynamic behaviour of particle clouds. In Eleventh Australasian Fluid Mechanics Conference, University of Tasmania, Hobart, 14–18 December, vol. 1 and 2, pp. 743–746.Google Scholar
Ruggaber, G. J.2000 The dynamics of particle clouds related to open-water sediment disposal. PhD thesis, Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA.Google Scholar
Scorer, R. S. 1957 Experiments on convection of isolated masses of buoyant fluid. J. Fluid Mech. 2 (6), 583–594.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Wen, F. & Nacamuli, A. 1996 The effect of the Rayleigh number on a particle cloud. In Hydrodynamics: Theory and Applications, vol. 1 and 2, pp. 1275–1280. Balkema.Google Scholar
Yang, C. T.2006 Erosion and sedimentation manual. Tech. Rep. Technical Service Center, US Bureau of Reclamation.Google Scholar
Zhao, B., Law, A. W. K., Adams, E. E., Shao, D. & Huang, Z. 2012 Effect of air release height on the formation of sediment thermal in water. J. Hydraul. Res. 50 (5), 532–540.Google Scholar
Zhao, B., Law, A. W. K., Huang, Z., Adams, E. E. & Lai, A. C. H. 2013a Behaviour of sediment clouds in waves. ASCE J. Waterway Port Coast. Ocean Engng 139 (1), 24–33.Google Scholar
Zhao, B., Law, A. W. K., Lai, A. C. H. & Adams, E. E. 2013b On the internal vorticity and density structures of miscible thermals. J. Fluid Mech 722, R5.Google Scholar