Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T16:48:08.310Z Has data issue: false hasContentIssue false
  • English
  • Français

Focusing deep-water surface gravity wave packets: wave breaking criterion in a simplified model

Published online by Cambridge University Press:  24 June 2019

Nick Pizzo Open the ORCID record for Nick Pizzo [Opens in a new window]  and
W. Kendall Melville
Nick Pizzo*
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 92037, USA
W. Kendall Melville
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 92037, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Geometric, kinematic and dynamic properties of focusing deep-water surface gravity wave packets are examined in a simplified model with the intent of deriving a wave breaking threshold parameter. The model is based on the spatial modified nonlinear Schrödinger equation of Dysthe (Proc. R. Soc. Lond. A, vol. 369 (1736), 1979, pp. 105–114). The evolution of initially narrow-banded and weakly nonlinear chirped Gaussian wave packets are examined, by means of a trial function and a variational procedure, yielding analytic solutions describing the approximate evolution of the packet width, amplitude, asymmetry and phase during focusing. A model for the maximum free surface gradient, as a function of $\unicode[STIX]{x1D716}$ and 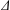$\unicode[STIX]{x1D6E5}$, for $\unicode[STIX]{x1D716}$ the linear prediction of the maximum slope at focusing and 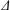$\unicode[STIX]{x1D6E5}$ the non-dimensional packet bandwidth, is proposed and numerically examined, indicating a quasi-self-similarity of these focusing events. The equations of motion for the fully nonlinear potential flow equations are then integrated to further investigate these predictions. It is found that a model of this form can characterize the bulk partitioning of 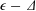$\unicode[STIX]{x1D716}-\unicode[STIX]{x1D6E5}$ phase space, between non-breaking and breaking waves, serving as a breaking criterion. Application of this result to better understanding air–sea interaction processes is discussed.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave breaking
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 238 - 259
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agrawal, G. P. 2007 Nonlinear Fiber Optics. Academic Press.Google Scholar
Akylas, T. R. 1989 Higher-order modulation effects on solitary wave envelopes in deep water. J. Fluid Mech. 198, 387–397.10.1017/S0022112089000182Google Scholar
Alber, I. E. 1978 The effects of randomness on the stability of two-dimensional surface wavetrains. Proc. R. Soc. Lond. A 363 (1715), 525–546.Google Scholar
Anderson, D. 1983 Variational approach to nonlinear pulse propagation in optical fibers. Phys. Rev. A 27 (6), 3135–3145.10.1103/PhysRevA.27.3135Google Scholar
Barthelemy, X., Banner, M. L., Peirson, W. L., Fedele, F., Allis, M. & Dias, F. 2018 On a unified breaking onset threshold for gravity waves in deep and intermediate depth water. J. Fluid Mech. 841, 463–488.10.1017/jfm.2018.93Google Scholar
Benjamin, T. B. & Feir, J. E. 1967 The disintegration of wave trains on deep water part 1. Theory. J. Fluid Mech. 27 (03), 417–430.10.1017/S002211206700045XGoogle Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods. Courier Corporation.Google Scholar
Bridges, T. J. 2004 Superharmonic instability, homoclinic torus bifurcation and water-wave breaking. J. Fluid Mech. 505, 153–162.10.1017/S0022112004008432Google Scholar
Camassa, R. & Holm, D. D. 1993 An integrable shallow water equation with peaked solitons. Phys. Rev. Lett. 71 (11), 1661.10.1103/PhysRevLett.71.1661Google Scholar
Cavaleri, L., Fox-Kemper, B. & Hemer, M. 2012 Wind waves in the coupled climate system. Bull. Am. Meteorol. Soc. 93 (11), 1651–1661.10.1175/BAMS-D-11-00170.1Google Scholar
Chandrasekhar, S. 2013 Hydrodynamic and Hydromagnetic Stability. Courier Corporation.Google Scholar
Chu, V. H. & Mei, C. C. 1970 On slowly-varying Stokes waves. J. Fluid Mech. 41 (04), 873–887.10.1017/S0022112070000988Google Scholar
Clamond, D., Francius, M., Grue, J. & Kharif, C. 2006 Long time interaction of envelope solitons and freak wave formations. Eur. J. Mech. (B/Fluids) 25 (5), 536–553.10.1016/j.euromechflu.2006.02.007Google Scholar
Craik, A. D. D. 2005 George Gabriel stokes on water wave theory. Annu. Rev. Fluid Mech. 37, 23–42.10.1146/annurev.fluid.37.061903.175836Google Scholar
Deike, L., Melville, W. K. & Popinet, S. 2016 Air entrainment and bubble statistics in breaking waves. J. Fluid Mech. 801, 91–129.10.1017/jfm.2016.372Google Scholar
Deike, L., Pizzo, N. E. & Melville, W. K. 2017 Lagrangian transport by breaking surface waves. J. Fluid Mech. 829, 364–391.10.1017/jfm.2017.548Google Scholar
Deike, L., Popinet, S. & Melville, W. K. 2015 Capillary effects on wave breaking. J. Fluid Mech. 769, 541–569.10.1017/jfm.2015.103Google Scholar
Derakhti, M., Banner, M. L. & Kirby, J. T. 2018 Predicting the breaking strength of gravity water waves in deep and intermediate depth. J. Fluid Mech. 848, R2-1–R2-12.10.1017/jfm.2018.352Google Scholar
Derakhti, M. & Kirby, J. T. 2016 Breaking-onset, energy and momentum flux in unsteady focused wave packets. J. Fluid Mech. 790, 553–581.10.1017/jfm.2016.17Google Scholar
Dold, J. W. 1992 An efficient surface-integral algorithm applied to unsteady gravity waves. J. Comput. Phys. 103 (1), 90–115.10.1016/0021-9991(92)90327-UGoogle Scholar
Dold, J. W. & Peregrine, D. H. 1986 Water-wave modulation. Coast. Engng Proc. 1 (20), 671–679.Google Scholar
Drazen, D. A., Melville, W. K. & Lenain, L. 2008 Inertial scaling of dissipation in unsteady breaking waves. J. Fluid Mech. 611, 307–332.10.1017/S0022112008002826Google Scholar
Duncan, J. H. 1981 An experimental investigation of breaking waves produced by a towed hydrofoil. Proc. R. Soc. Lond. A 377 (1770), 331–348.Google Scholar
Dyachenko, A. I., Kachulin, D. I. & Zakharov, V. E. 2017 Super compact equation for water waves. J. Fluid Mech. 828, 661–679.10.1017/jfm.2017.529Google Scholar
Dyachenko, A. I. & Zakharov, V. E. 2011 Compact equation for gravity waves on deep water. JETP Lett. 93 (12), 701.10.1134/S0021364011120058Google Scholar
Dysthe, K. B. 1979 Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. A 369 (1736), 105–114.Google Scholar
Fedele, F. 2014 On certain properties of the compact Zakharov equation. J. Fluid Mech. 748, 692–711.10.1017/jfm.2014.192Google Scholar
Gramstad, O. & Trulsen, K. 2011 Hamiltonian form of the modified nonlinear Schrödinger equation for gravity waves on arbitrary depth. J. Fluid Mech. 670, 404–426.10.1017/S0022112010005355Google Scholar
Janssen, P. A. E. M. 1983 On a fourth-order envelope equation for deep-water waves. J. Fluid Mech. 126, 1–11.10.1017/S0022112083000014Google Scholar
Janssen, P. A. E. M. 2003 Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 33 (4), 863–884.10.1175/1520-0485(2003)33<863:NFIAFW>2.0.CO;22.0.CO;2>Google Scholar
Khait, A. & Shemer, L. 2018 On the kinematic criterion for the inception of breaking in surface gravity waves: fully nonlinear numerical simulations and experimental verification. Phys. Fluids 30 (5), 057103.10.1063/1.5026394Google Scholar
Kit, E. & Shemer, L. 2002 Spatial versions of the Zakharov and Dysthe evolution equations for deep-water gravity waves. J. Fluid Mech. 450, 201–205.10.1017/S0022112001006498Google Scholar
Lo, E. & Mei, C. C. 1985 A numerical study of water-wave modulation based on a higher-order nonlinear Schrödinger equation. J. Fluid Mech. 150, 395–416.10.1017/S0022112085000180Google Scholar
Longuet-Higgins, M. S. 1974 Breaking waves in deep or shallow water. In Proceedings of the 10th Conference on Naval Hydrodynamics, vol. 597. Massachusetts Institute of Technology.Google Scholar
Longuet-Higgins, M. S. 1978 The instabilities of gravity waves of finite amplitude in deep water. I. Superharmonics. Proc. R. Soc. Lond. A 360 (1703), 471–488.Google Scholar
Longuet-Higgins, M. S. & Dommermuth, D. G. 1997 Crest instabilities of gravity waves. Part 3. Nonlinear development and breaking. J. Fluid Mech. 336, 33–50.10.1017/S002211209600403XGoogle Scholar
Longuet-Higgins, M. S. & Stewart, R. W. 1964 Radiation stresses in water waves; a physical discussion, with applications. Deep-Sea Res. Oceanogr. Abstracts 11 (4), 529–562.10.1016/0011-7471(64)90001-4Google Scholar
Luke, J. C. 1967 A variational principle for a fluid with a free surface. J. Fluid Mech. 27 (02), 395–397.10.1017/S0022112067000412Google Scholar
Lushnikov, P. M., Dyachenko, S. A. & Silantyev, D. A. 2017 New conformal mapping for adaptive resolving of the complex singularities of Stokes wave. Proc. R. Soc. Lond. A 473 (2202), 20170198.Google Scholar
McIntyre, M. E. 1981 On the wave momentum myth. J. Fluid Mech. 106, 331–347.10.1017/S0022112081001626Google Scholar
McLean, J. W., Ma, Y. C., Martin, D. U., Saffman, P. G. & Yuen, H. C. 1981 Three-dimensional instability of finite-amplitude water waves. Phys. Rev. Lett. 46 (13), 817.10.1103/PhysRevLett.46.817Google Scholar
Melville, W. K. 1982 The instability and breaking of deep-water waves. J. Fluid Mech. 115, 165–185.10.1017/S0022112082000706Google Scholar
Melville, W. K. 1983 Wave modulation and breakdown. J. Fluid Mech. 128, 489–506.10.1017/S0022112083000579Google Scholar
Melville, W. K. 1996 The role of surface wave breaking in air–sea interaction. Annu. Rev. Fluid Mech. 28, 279–321.10.1146/annurev.fl.28.010196.001431Google Scholar
Melville, W. K. & Rapp, R. J. 1985 Momentum flux in breaking waves. Nature 317 (6037), 514–516.10.1038/317514a0Google Scholar
Miles, J. W. 1977 On Hamilton’s principle for surface waves. J. Fluid Mech. 83 (01), 153–158.10.1017/S0022112077001104Google Scholar
Onorato, M., Osborne, A. R., Serio, M. & Bertone, S. 2001 Freak waves in random oceanic sea states. Phys. Rev. Lett. 86 (25), 5831.10.1103/PhysRevLett.86.5831Google Scholar
Perlin, M., Choi, W. & Tian, Z. 2013 Breaking waves in deep and intermediate waters. Annu. Rev. Fluid Mech. 45, 115–145.10.1146/annurev-fluid-011212-140721Google Scholar
Phillips, O. M. 1977 The Dynamics of The Upper Ocean. Cambridge University Press.Google Scholar
Phillips, O. M. 1981 Wave interactions-the evolution of an idea. J. Fluid Mech. 106, 215–227.10.1017/S0022112081001572Google Scholar
Phillips, O. M. 1985 Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J. Fluid Mech. 156 (1), 505–531.10.1017/S0022112085002221Google Scholar
Pizzo, N. E. 2017 Surfing surface gravity waves. J. Fluid Mech. 823, 316–328.10.1017/jfm.2017.314Google Scholar
Pizzo, N. E. & Melville, W. K. 2013 Vortex generation by deep-water breaking waves. J. Fluid Mech. 734, 198–218.10.1017/jfm.2013.453Google Scholar
Pizzo, N. E. & Melville, W. K. 2016 Wave modulation: the geometry, kinematics, and dynamics of surface-wave packets. J. Fluid Mech. 803, 275–291.10.1017/jfm.2016.469Google Scholar
Pizzo, N. E., Melville, W. K. & Deike, L. 2016 Current generation by deep-water wave breaking. J. Fluid Mech. 803, 292–312.10.1017/jfm.2016.473Google Scholar
Pizzo, N. E., Melville, W. K. & Deike, L. 2019 Lagrangian transport by non-breaking and breaking deep-water waves at the ocean surface. J. Phys. Oceanogr. 49 (4), 983–992.10.1175/JPO-D-18-0227.1Google Scholar
Pomeau, Y., Le Berre, M., Guyenne, P. & Grilli, S. 2008 Wave-breaking and generic singularities of nonlinear hyperbolic equations. Nonlinearity 21 (5), T61.10.1088/0951-7715/21/5/T01Google Scholar
Rapp, R. J. & Melville, W. K. 1990 Laboratory measurements of deep-water breaking waves. Phil. Trans. R. Soc. Lond. A 331, 735–800.Google Scholar
Romero, L., Melville, W. K. & Kleiss, J. M. 2012 Spectral energy dissipation due to surface wave breaking. J. Phys. Oceanogr. 42 (9), 1421–1444.10.1175/JPO-D-11-072.1Google Scholar
Saket, A., Peirson, W. L., Banner, M. L., Barthelemy, X. & Allis, M. J. 2017 On the threshold for wave breaking of two-dimensional deep water wave groups in the absence and presence of wind. J. Fluid Mech. 811, 642–658.10.1017/jfm.2016.776Google Scholar
Seliger, R. L. 1968 A note on the breaking of waves. Proc. R. Soc. Lond. A 303 (1475), 493–496.Google Scholar
Shemer, L., Kit, E. & Jiao, H. 2002 An experimental and numerical study of the spatial evolution of unidirectional nonlinear water-wave groups. Phys. Fluids 14 (10), 3380–3390.10.1063/1.1501908Google Scholar
Stokes, G. G. 1880 On the Theory of Oscillatory Waves, Appendix B. Cambridge University Press.Google Scholar
Sulem, C. & Sulem, P.-L. 1999 The Nonlinear Schrödinger Equation: Self-Focusing and Wave Collapse, vol. 139. Springer.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Melville, W. K. 2007 Surface gravity wave effects in the oceanic boundary layer: large-eddy simulation with vortex force and stochastic breakers. J. Fluid Mech. 593, 405–452.10.1017/S002211200700897XGoogle Scholar
Sutherland, P. & Melville, W. K. 2013 Field measurements and scaling of ocean surface wave-breaking statistics. Geophys. Res. Lett. 40 (12), 3074–3079.10.1002/grl.50584Google Scholar
Sutherland, P. & Melville, W. K. 2015 Field measurements of surface and near-surface turbulence in the presence of breaking waves. J. Phys. Oceanogr. 45 (4), 943–965.10.1175/JPO-D-14-0133.1Google Scholar
Tanaka, M. 1983 The stability of steep gravity waves. J. Phys. Soc. Japan 52 (9), 3047–3055.10.1143/JPSJ.52.3047Google Scholar
Temme, N. M. 2010 Error functions, Dawson’s and Fresnel integrals. In NIST Handbook of Mathematical Functions, pp. 159–171. Cambridge University Press.Google Scholar
Tian, Z., Perlin, M. & Choi, W. 2010 Energy dissipation in two-dimensional unsteady plunging breakers and an eddy viscosity model. J. Fluid Mech. 655, 217–257.10.1017/S0022112010000832Google Scholar
Titchmarsh, E. C. 1948 Introduction to the Theory of Fourier Integrals. Clarendon Press.Google Scholar
Trulsen, K. 2006 Weakly Nonlinear and Stochastic Properties of Ocean Wave Fields. Application to An Extreme Wave Event, Springer.10.1007/978-3-211-69356-8_2Google Scholar
Trulsen, K. & Dysthe, K. B. 1997 Frequency downshift in three-dimensional wave trains in a deep basin. J. Fluid Mech. 352, 359–373.10.1017/S0022112097007416Google Scholar
Trulsen, K., Kliakhandler, I., Dysthe, K. B. & Velarde, M. G. 2000 On weakly nonlinear modulation of waves on deep water. Phys. Fluids 12 (10), 2432–2437.10.1063/1.1287856Google Scholar
Whitham, G. B. 1965 A general approach to linear and non-linear dispersive waves using a Lagrangian. J. Fluid Mech. 22 (02), 273–283.10.1017/S0022112065000745Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar
Yamada, H. 1957 Highest waves of permanent type on the surface of deep water. Report Res. Inst. Appl. Mech. Kyushu Univ. 5, 37–52.Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9 (2), 190–194.10.1007/BF00913182Google Scholar