Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T15:17:23.952Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow topology of helical vortices

Published online by Cambridge University Press:  12 March 2018

Oscar Velasco Fuentes Open the ORCID record for Oscar Velasco Fuentes [Opens in a new window]
Oscar Velasco Fuentes*
Affiliation:
Departamento de Oceanografía Física, CICESE, Ensenada, B.C. 22860, México
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Equal coaxial symmetrically located helical vortices translate and rotate steadily while preserving their shape and relative position if they move in an unbounded inviscid incompressible fluid. In this paper, the linear and angular velocities of this set of vortices (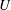$U$ and 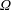$\unicode[STIX]{x1D6FA}$ respectively) are computed as the sum of the mutually induced velocities found by Okulov (J. Fluid Mech., vol. 521, 2004, pp. 319–342) and the self-induced velocities found by Velasco Fuentes (J. Fluid Mech., vol. 836 2018). Numerical computations of the velocities using the Helmholtz integral and the Biot–Savart law, as well as numerical simulations of the flow evolution under the Euler equations, are used to verify that the theoretical results are accurate for 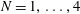$N=1,\ldots ,4$ vortices over a broad range of values of the pitch and radius of the vortices. An analysis of the flow topology in a reference system that translates with velocity 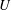$U$ and rotates with angular velocity 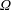$\unicode[STIX]{x1D6FA}$ serves to determine the capacity of the vortices to transport fluid.

JFM classification

Mathematical Foundations: Mathematical Foundations Mathematical Foundations: Topological fluid dynamics Vortex Flows: Vortex Flows
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , R2
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, M. & Brøns, M. 2014 Topology of helical fluid flow. Eur. J. Appl. Mech. 25, 275–396.Google Scholar
Boersma, J. & Wood, D. H. 1999 On the self-induced motion of a helical vortex. J. Fluid Mech. 384, 263–280.Google Scholar
Fitzgerald, G. F. 1899 On a hydro-dynamical hypothesis as to electro-magnetic actions. Sci. Proc. Dublin R. Soc. 9, 55–59.Google Scholar
Hardin, J. C. 1982 The velocity field induced by a helical vortex filament. Phys. Fluids 25, 1949–1952.CrossRefGoogle Scholar
Joukowsky, N. E. 1912 Vihrevaja teorija grebnogo vinta. Trudy Otdeleniya Fizicheskikh Nauk Obshchestva Lubitelei Estestvoznaniya 16, 1–31; French translation in Théorie tourbillonnaire de l’hélice propulsive (Gauthier-Villars, Paris, 1929) 1–47.Google Scholar
Kawada, S.1939 Calculation of Induced Velocity by Helical Vortices and Its Application to Propeller Theory. Report of the Aeronautical Research Institute 14. Aeronautical Research Institute, Tokyo Imperial University.Google Scholar
Lamb, H. 1923 The magnetic field of a helix. Proc. Camb. Phil. Soc. 21, 477–481.Google Scholar
Mezić, I., Leonard, A. & Wiggins, S. 1998 Regular and chaotic particle motion near a helical vortex filament. Physica D 111, 179–201.Google Scholar
Okulov, V. L. 2004 On the stability of multiple helical vortices. J. Fluid Mech. 521, 319–342.CrossRefGoogle Scholar
Okulov, V. L. & Sørensen, J. N. 2007 Stability of helical tip vortices in a rotor far wake. J. Fluid Mech. 576, 1–25.Google Scholar
Ricca, R. L. 1994 The effect of torsion on the motion of a helical vortex filament. J. Fluid Mech. 273, 241–259.Google Scholar
Saffman, P. G. 1995 Vortex Dynamics. Cambridge University Press.Google Scholar
Suaza Jaque, R. & Velasco Fuentes, O. 2017 Reconnection of orthogonal cylindrical vortices. Eur. J. Mech. (B/Fluids) 62, 51–56.Google Scholar
Thomson, W. (Lord Kelvin) 1875 Vortex statics. Proc. R. Soc. Edin. 9, 59–73.Google Scholar
Velasco Fuentes, O. 2010 Chaotic streamlines in the flow of knotted and unknotted vortices. Theor. Comput. Fluid Dyn. 24, 189–193.CrossRefGoogle Scholar
Velasco Fuentes, O. 2018 Motion of a helical vortex. J. Fluid Mech. 836, R1.Google Scholar
Velasco Fuentes, O. & Romero Arteaga, A. 2011 Quasi-steady linked vortices with chaotic streamlines. J. Fluid Mech. 687, 571–583.Google Scholar
Wood, D. H. & Boersma, J. 2001 On the motion of multiple helical vortices. J. Fluid Mech. 447, 149–171.Google Scholar