Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tang, Guoqiang
Cheng, Liang
Tong, Feifei
Lu, Lin
and
Zhao, Ming
2017.
Modes of synchronisation in the wake of a streamwise oscillatory cylinder.
Journal of Fluid Mechanics,
Vol. 832,
Issue. ,
p.
146.
Xiong, Chengwang
Cheng, Liang
Tong, Feifei
and
An, Hongwei
2018.
Oscillatory flow regimes for a circular cylinder near a plane boundary.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
127.
Ren, Chengjiao
Cheng, Liang
Tong, Feifei
Xiong, Chengwang
and
Chen, Tingguo
2019.
Oscillatory flow regimes around four cylinders in a diamond arrangement.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
955.
Huang, Zhenhua
Huang, Shijie
and
Xu, Conghao
2020.
Characteristics of the flow around a circular OWC-type wave energy converter supported by a bottom-sitting C-shaped structure.
Applied Ocean Research,
Vol. 101,
Issue. ,
p.
102228.
Zhang, Yuhang
Wang, Rui
Chen, Yaoran
Bao, Yan
Han, Zhaolong
Zhou, Dai
Ping, Huan
Fu, Shixiao
and
Zhao, Yongsheng
2020.
Three-dimensional wake transition in the flow over four square cylinders at low Reynolds numbers.
AIP Advances,
Vol. 10,
Issue. 1,
Li, Ming
Li, Qiusheng
and
Shi, Haoyun
2021.
Aerodynamic pressures on a 5:1 rectangular cylinder in sinusoidal streamwise oscillatory flows with non-zero mean velocities.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 208,
Issue. ,
p.
104440.
Li, Ang
Shi, Shengmin
and
Fan, Dixia
2022.
Fluid Forces and Vortex Patterns of an Oscillating Cylinder Pair in Still Water With Both Fixed Side-by-Side and Tandem Configurations.
Journal of Offshore Mechanics and Arctic Engineering,
Vol. 144,
Issue. 2,
Wright, Christopher Simon
Yoshimoto, Haruki
Wada, Ryota
and
Takagi, Ken
2022.
Surge slow drift viscous drag damping of an advanced spar: A numerical–experimental method for variable damping rates.
Ocean Engineering,
Vol. 266,
Issue. ,
p.
112696.
Li, Ming
Li, Qiusheng
Shi, Hao-Yun
and
Li, Ming-Shui
2022.
Large-Scale Gust Effect on Aerodynamic Pressures and Forces on a Square Cylinder.
SSRN Electronic Journal ,
Lu, Lin
Zhou, Zhongbing
and
Zhang, Cheng
2023.
Flow regime identification and flow instability analysis of oscillatory flows over twin circular cylinders.
Physics of Fluids,
Vol. 35,
Issue. 10,
Li, Ming
Li, Qiu-Sheng
Shi, Hao-Yun
and
Li, Ming-Shui
2023.
Large-scale sinusoidal gust effect on aerodynamic pressures and forces on a square cylinder.
Journal of Fluids and Structures,
Vol. 120,
Issue. ,
p.
103917.
Chang, Wen-Yi
and
Constantinescu, George
2023.
Oscillatory flow around a vertical circular cylinder placed in an open channel: coherent structures, sediment entrainment potential and drag forces.
Journal of Fluid Mechanics,
Vol. 964,
Issue. ,
Sun, Shuzheng
Yang, Wanqing
Liu, Shengnan
Li, Pei
and
Ong, Muk Chen
2024.
Computational fluid dynamics simulations of a near-wall rectangular cylinder in an oscillatory flow.
Ocean Engineering,
Vol. 304,
Issue. ,
p.
117776.
Wang, Xincong
Li, Qiusheng
Lu, Bin
and
Han, Xuliang
2024.
Aerodynamic characteristics of a square cylinder in streamwise sinusoidal flows.
Physics of Fluids,
Vol. 36,
Issue. 7,
Wang, Wen-Quan
Luo, Jia-Ling
and
Yan, Yan
2024.
Hydrodynamic characteristics of hyperbolic cylinder under periodic pulsating flow at moderately high Reynolds number (Re=3900).
Ocean Engineering,
Vol. 303,
Issue. ,
p.
117653.
Sun, Shuzheng
Li, Pei
Liu, Shengnan
and
Yang, Wanqing
2024.
Numerical simulations of the effects of KC number and entrapped water on the subsea cover hydrodynamic characteristics.
Ships and Offshore Structures,
p.
1.
Chang, Wen-Yi
and
Constantinescu, George
2025.
Flow structure around a vertical cylinder placed in an open channel under combined wave-current flows.
Physical Review Fluids,
Vol. 10,
Issue. 2,
Wang, Xinru
Zhu, Jianxun
Holmedal, Lars Erik
Myrhaug, Dag
and
Wang, Hong
2025.
Numerical investigation of oscillatory flow regimes around an elliptic cylinder at low Keulegan-Carpenter and Reynolds numbers.
Physical Review Fluids,
Vol. 10,
Issue. 2,
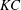 $KC$) and low Reynolds number (
$KC$) and low Reynolds number (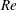 $Re$) for a square cross-section cylinder with its face normal to the oscillatory flow. Based on the numerical simulations a map of flow regimes is formed and compared to the map of flow around an oscillating circular cylinder by Tatsuno & Bearman (J. Fluid Mech., vol. 211, 1990, pp. 157–182). Two new flow regimes have been observed, namely A
$Re$) for a square cross-section cylinder with its face normal to the oscillatory flow. Based on the numerical simulations a map of flow regimes is formed and compared to the map of flow around an oscillating circular cylinder by Tatsuno & Bearman (J. Fluid Mech., vol. 211, 1990, pp. 157–182). Two new flow regimes have been observed, namely A $^{\prime }$ and F
$^{\prime }$ and F $^{\prime }$. The regime A
$^{\prime }$. The regime A $^{\prime }$ found at low
$^{\prime }$ found at low 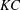 $KC$ is characterised by the transverse convection of fluid particles perpendicular to the motion; and the regime F
$KC$ is characterised by the transverse convection of fluid particles perpendicular to the motion; and the regime F $^{\prime }$ found at high
$^{\prime }$ found at high 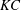 $KC$ shows a quasi-periodic feature with a well-defined secondary period, which is larger than the oscillation period. The Floquet analysis demonstrates that when the two-dimensional flow breaks the reflection symmetry about the axis of oscillation, the quasi-periodic instability and the synchronous instability with the imposed oscillation occur alternately for the square cylinder along the curve of marginal stability. This alternate pattern in instabilities leads to four distinct flow regimes. When compared to the vortex shedding in otherwise unidirectional flow, the two quasi-periodic flow regimes are observed when the oscillation frequency is close to the Strouhal frequency (or to half of it). Both the flow regimes and marginal stability curve shift in the
$KC$ shows a quasi-periodic feature with a well-defined secondary period, which is larger than the oscillation period. The Floquet analysis demonstrates that when the two-dimensional flow breaks the reflection symmetry about the axis of oscillation, the quasi-periodic instability and the synchronous instability with the imposed oscillation occur alternately for the square cylinder along the curve of marginal stability. This alternate pattern in instabilities leads to four distinct flow regimes. When compared to the vortex shedding in otherwise unidirectional flow, the two quasi-periodic flow regimes are observed when the oscillation frequency is close to the Strouhal frequency (or to half of it). Both the flow regimes and marginal stability curve shift in the 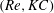 $(Re,KC)$-space compared to the oscillatory flow around a circular cylinder and this shift appears to be consistent with the change in vortex formation time associated with the lower Strouhal frequency of the square cylinder.
$(Re,KC)$-space compared to the oscillatory flow around a circular cylinder and this shift appears to be consistent with the change in vortex formation time associated with the lower Strouhal frequency of the square cylinder.


