Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T15:38:36.970Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow past finite cylinders of constant curvature

Published online by Cambridge University Press:  05 January 2018

Jessica K. Shang Open the ORCID record for Jessica K. Shang [Opens in a new window] ,
H. A. Stone  and
A. J. Smits
Jessica K. Shang*
Affiliation:
Department of Mechanical Engineering, University of Rochester, Rochester, NY 14627, USA
H. A. Stone
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
A. J. Smits
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Wake visualization experiments were conducted on a finite curved cylinder whose plane of curvature is aligned with the free stream. The stagnation face of the cylinder is oriented concave or convex to the flow at 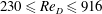$230\leqslant Re_{D}\leqslant 916$, where 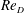$Re_{D}$ is the cylinder Reynolds number and the curvature is constant and ranges from a straight cylinder to a quarter-ring. While the magnitude of the local angle of incidence to the flow is the same for both orientations, the contrast in their wakes demonstrates a violation of a common approximation known as the ‘independence principle’ for curved cylinders. Vortex shedding always occurred for the convex-oriented cylinder for the Reynolds-number range investigated, along most of the cylinder span, at a constant vortex shedding angle. In contrast, a concave-oriented cylinder could exhibit multiple concurrent wake regimes along its span: two shedding regimes (oblique, normal) and two non-shedding regimes. The occurrence of these wake regimes depended on the curvature, aspect ratio and Reynolds number. In some cases, vortex shedding was entirely suppressed, particularly at higher curvatures. In the laminar wake regime, increasing the curvature or decreasing the aspect ratio restricts vortex shedding to smaller regions along the span of the cylinder. Furthermore, the local angle of incidence where vortex shedding occurs is self-similar across cylinders of the same aspect ratio and varying curvature. After the wake transitions to turbulence, the vortex shedding extends along most of the cylinder span. The difference in the wakes between the concave and convex orientations is attributed to the spanwise flow induced by the finite end conditions, which reduces the generation of spanwise vorticity and increases the incidence of non-shedding and obliquely shedding wakes for the concave cylinder.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Separated flows Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 837 , 25 February 2018 , pp. 896 - 915
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afghan, I., Moulinec, C. & Laurence, D. 2006 Large eddy simulation of flow over a vertically mounted finite cylinder on a flat plate. In Conference on Modeling Fluid Flow (CMFF’06) The 13th International Conference on Fluid Flow Technologies, Budapest, Hungary, pp. 193–200.Google Scholar
Ahmed, A. 2001 Flow field of a curved cylinder. In 39th Aerospace Sciences Meeting and Exhibit. American Institute of Aeronautics and Astronautics.Google Scholar
Degani, D. & Schiff, L. B. 1991 Numerical simulation of the effect of spatial disturbances on vortex asymmetry. AIAA J. 29 (3), 344–352.Google Scholar
Gallardo, J. P., Andersson, H. I. & Pettersen, B. 2014 Turbulent wake behind a curved circular cylinder. J. Fluid Mech. 742, 192–229.Google Scholar
Hammache, M. & Gharib, M. 1991 An experimental study of the parallel and oblique vortex shedding from circular cylinders. J. Fluid Mech. 232, 567–590.Google Scholar
Hanson, A. 1966 Vortex shedding from yawed cylinders. AIAA J. 4 (4), 738–740.Google Scholar
Hoang, N. & Telionis, D. 1991 The dynamic character of the wake of an axisymmetric body at an angle of attack. AIAA Paper 91-3268.Google Scholar
Hunt, B. 1982 Asymmetric vortex forces and wakes on slender bodies. AIAA Paper 82-1336.Google Scholar
Lamont, P. & Hunt, B. 1976 Pressure and force distributions on a sharp-nosed circular cylinder at large angles of inclination to a uniform subsonic stream. J. Fluid Mech. 76 (03), 519–559.Google Scholar
Lowson, M. & Ponton, A. 1992 Symmetry breaking in vortex flows on conical bodies. AIAA J. 30 (6), 1576–1583.Google Scholar
Miliou, A., De Vecchi, A., Sherwin, S. & Graham, J. 2007 Wake dynamics of external flow past a curved circular cylinder with the free stream aligned with the plane of curvature. J. Fluid Mech. 592, 89–115.Google Scholar
Montividas, R., Reisenthel, P. & Nagib, H. 1989 The scaling and control of vortex geometry behind pitching cylinders. In 2nd Shear Flow Conference, American Institute of Aeronautics and Astronautics.Google Scholar
Moskovitz, C. A., Hall, R. M. & DeJarnette, F. R. 1989 Effects of Nose Bluntness, Roughness and Surface Perturbations on the Symmetric Flow Past Slender Bodies at Large Angles of Attack. American Institute of Aeronautics and Astronautics.Google Scholar
Noack, B. R. & Eckelmann, H. 1994 A global stability analysis of the steady and periodic cylinder wake. J. Fluid Mech. 270, 297–330.Google Scholar
Park, C.-W. & Lee, S.-J. 2000 Free end effects on the near wake flow structure behind a finite circular cylinder. J. Wind Engng Ind. Aerodyn. 88, 231–246.Google Scholar
Ramberg, S. 1983 The effects of yaw and finite length upon the vortex wakes of stationary and vibrating circular cylinders. J. Fluid Mech. 128, 81–107.Google Scholar
Roshko, A.1954 On the development of turbulent wakes from vortex streets. NACA Rep. 1191.Google Scholar
Sirovich, L. & Kirby, M. 1987 Low-dimensional procedure for the characterization of human faces. J. Opt. Soc. Am. A 4 (3), 519–524.Google Scholar
Slaouti, A. & Gerrard, J. H. 1981 An experimental investigation of the end effects on the wake of a circular cylinder towed through water at low Reynolds numbers. J. Fluid Mech. 112, 297–314.Google Scholar
Smits, A. & Lim, T. 2000 Flow Visualization: Techniques and Examples. Imperial College Press.Google Scholar
Surry, J.1965 Experimental investigation of the characteristics of flow about curved circular cylinders. Tech. Rep. DTIC Document.Google Scholar
Van Atta, C. 1968 Experiments on vortex shedding from yawed circular cylinders. AIAA J. 6, 931–933.Google Scholar
Wang, H., Razali, S. M., Zhou, T., Zhou, Y. & Cheng, L. 2011 Streamwise evolution of an inclined cylinder wake. Exp. Fluids 51 (2), 553–570.Google Scholar
Williamson, C. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.Google Scholar
Williamson, C. 1996a Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Williamson, C. H. 1988 Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 31 (10), 2742–2744.Google Scholar
Williamson, C. H. K. 1996b Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Zeiger, M. D., Vlachos, P. P. & Telionis, D. P. 2001 The dynamic character of the vortical flow over a slender axisymmetric body. AIAA Paper 2001-1036.Google Scholar
Zhao, M., Cheng, L. & Zhou, T. 2009 Direct numerical simulation of three-dimensional flow past a yawed circular cylinder of infinite length. J. Fluids Struct. 25 (5), 831–847.Google Scholar
Zhou, T., Razali, S. M., Zhou, Y., Chua, L. & Cheng, L. 2009 Dependence of the wake on inclination of a stationary cylinder. Exp. Fluids 46 (6), 1125–1138.Google Scholar
Zhou, T., Wang, H., Razali, S., Zhou, Y. & Cheng, L. 2010 Three-dimensional vorticity measurements in the wake of a yawed circular cylinder. Phys. Fluids 22 (1), 015108.Google Scholar
Zilliac, G., Degani, D. & Tobak, M. 1991 Asymmetric vortices on a slender body of revolution. AIAA J. 29 (5), 667–675.Google Scholar

Shang et al. movie 1

Wake visualizations for a cylinder of α = 75○ and L/D=30 at ReD = 468 in a convex orientation. Flow is from left to right.

Download Shang et al. movie 1(Video)
Video 5.8 MB

Shang et al. movie 2

Wake visualizations for a cylinder of α = 75○ and L/D=30 at ReD = 468 in a concave orientation. Flow is from left to right.

Download Shang et al. movie 2(Video)
Video 5.5 MB