Article contents
Flapping dynamics of a flag in the presence of thermal convection
Published online by Cambridge University Press: 15 May 2020
Abstract
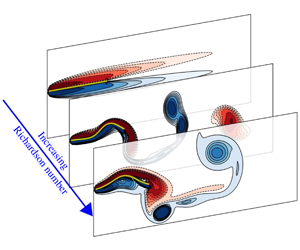
The flow-induced flapping dynamics of a flexible two-dimensional heated flag in the mixed convection regime is studied here. A linear stability analysis is first used to predict the flutter stability using three dimensionless parameters of reduced flow velocity, mass ratio and Richardson number. This is followed by fully coupled computational simulations to investigate the role of flapping motion on the flag’s thermal performance. The results show that an increase of Richardson number has a non-monotonic stabilizing effect on the flag response over the range of reduced velocities. The distinct flapping response regimes previously reported in the literature are recovered here and expanded upon by finding new flapping modes within the limit-cycle regime. It is found that mode switching is associated not only with the frequency response of the system but is also highly coupled to the flag’s thermal performance. The average Nusselt number over the structure attains the highest value when the flag vibrates in its higher fluttering mode, wherein it shows a higher sensitivity to Richardson number. We also report the correlations for the Nusselt number for the different flapping modes and identify an unexpected dependency of the modes on the flag inertia in the presence of the thermal effects.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 6
- Cited by


