Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T10:12:00.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Filling box flows in porous media

Published online by Cambridge University Press:  09 October 2015

Chunendra K. Sahu  and
M. R. Flynn
Chunendra K. Sahu*
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, AB, T6G 2G8, Canada
M. R. Flynn
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, AB, T6G 2G8, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report upon a theoretical and experimental investigation of a porous medium ‘filling box’ flow by specifically examining the details of the laminar descending plume and its outflow in a control volume having an impermeable bottom boundary and sidewalls. The plume outflow initially comprises a pair of oppositely directed gravity currents. The gravity currents propagate horizontally until they reach the lateral sidewalls at 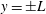$y=\pm L$. The flow then becomes of filling box type, with a vertically ascending ‘first front’ separating discharged plume fluid below from ambient fluid above. The flow details are described analytically by first deriving a new similarity solution for Darcy plumes with 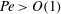$\mathit{Pe}>O(1)$, where 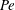$\mathit{Pe}$ is the Péclet number. From the similarity solution so obtained, we then derive expressions for the plume volume flux and mean reduced gravity as functions of the vertical distance from the source. Regarding the plume outflow, a similarity solution adopted from Huppert & Woods (J. Fluid Mech., vol. 292, 1995, pp. 55–69) describes the height and front speed of the gravity currents, whereas a semi-implicit finite difference scheme is used to predict the first front elevation versus time and horizontal distance. As with high-Reynolds-number filling box flows, that studied here is an example of a coupled problem: the gravity current source conditions are prescribed by the plume volume flux and mean reduced gravity. Conversely, discharged plume fluid may be re-entrained into the plume, be it soon or long after reaching the bottom impermeable boundary. To corroborate our model predictions, analogue laboratory experiments are performed with fresh water and salt water as the working fluids. Our experiments consider as independent variables the porous medium bead diameter and the plume source volume flux and reduced gravity. Predictions for the gravity current front position and height compare favourably against analogue measured data. Good agreement is likewise noted when considering either the mean elevation or the profile of the first front. Results from this study may be adopted in modelling geological plumes. For example, our equations can be used to predict the time required for discharged plume fluid to return to the point of injection in the case of aquifers closed on the sides and below by impermeable boundaries.

JFM classification

Convection: Convection in porous media Geophysical and Geological Flows: Gravity currents Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 782 , 10 November 2015 , pp. 455 - 478
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acton, J. M., Huppert, H. E. & Worster, M. G. 2001 Two-dimensional viscous gravity currents flowing over a deep porous medium. J. Fluid Mech. 440, 359–380.Google Scholar
Baines, S. J. & Worden, R. H. 2004 Geological storage of carbon dioxide. Geol. Soc. Lond. 233, 1–6.Google Scholar
Baines, W. D. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37, 51–80.Google Scholar
Bear, J. 1972 Dynamics of Fluids in Porous Medium. American Elsevier.Google Scholar
Bear, J. & Verruijt, A. 1987 Modelling Groundwater Flow and Pollution. D. Reid.Google Scholar
Bickle, M., Chadwick, A., Huppert, H. E., Hallworth, M. & Lyle, S. 2007 Modelling carbon dioxide accumulation at Sleipner: implications for underground carbon storage. Earth Planet. Sci. Lett. 255, 164–176.Google Scholar
Britter, B. E. 1979 The spread of a negatively buoyant plume in a calm environment. Atmos. Environ. 13, 1241–1247.Google Scholar
Caulfield, C. P. & Woods, A. W. 2002 The mixing in a room by a localized finite-mass-flux source of buoyancy. J. Fluid Mech. 471, 33–50.Google Scholar
Causon, D. M. & Mingham, C. G. 2010 Introductory Finite Difference Methods for PDEs. Ventus.Google Scholar
Chen, K. S. & Ho, J. R. 1986 Effect of flow inertia on vertical natural convection in saturated porous media. Intl J. Heat Mass Transfer 29, 753–759.Google Scholar
Delgado, J. M. P. Q 2007 Longitudinal and transverse dispersion in porous media. IChemE 85 (A9), 1245–1252.Google Scholar
Dullien, F. A. L. 1992 Porous Medium Fluid Transport and Pore Structures. Academic.Google Scholar
Ennis-King, J. & Paterson, L. 2003 Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. Soc. Petroleum Engineers SPE 84344, 1–12.Google Scholar
Germeles, A. E. 1975 Forced plumes and mixing of liquids in tanks. J. Fluid Mech. 71, 601–623.Google Scholar
Guin, J. A., Kessler, D. P. & Greenkorn, R. A. 1972 The dispersion tensor in anisotropic porous media. Ind. Engng Chem. Fundam. 11–4, 477–482.CrossRefGoogle Scholar
Happel, J. & Brenner, H. 1991 Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media, 2nd edn. Kluwer Academic.Google Scholar
Houseworth, J. E.1984 Longitudinal dispersion in non-uniform, isotropic porous media. Tech. Rep. KH-R-45. California Institute Of Technology, Pasadena, CA.Google Scholar
Hughes, G. O. & Griffiths, R. W. 2006 A simple convective model of the global overturning circulation, including effects of entrainment into sinking regions. Ocean Model. 12, 46–79.CrossRefGoogle Scholar
Hunt, G. R. & Kaye, N. G. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
Kaye, N. B. & Hunt, G. R. 2007 Overturning in a filling box. J. Fluid Mech. 576, 297–323.Google Scholar
Khachikian, C. & Harmon, T. C. 2000 Nonaqueous phase liquid dissolution in porous media: current state of knowledge and research needs. Transp. Porous Media 38, 3–28.Google Scholar
Kueper, B. H., Wealthall, G. P., Smith, J. W. N., Leharne, S. A. & Lerner, D. N.2003 An illustrated handbook of DNAPL transport and fate in the subsurface. Tech. Rep. R&D Publication 133. Environment Agency.Google Scholar
Lai, F. C. 1991 Non-Darcy convection from a line source of heat in a saturated porous medium. Intl Commun. Heat Mass Transfer 18, 445–457.Google Scholar
Linden, P. F., Lane-Serff, G. F. & Smeed, D. A. 1990 Emptying filling boxes: the fluid mechanics of natural ventilation. J. Fluid Mech. 212, 309–335.Google Scholar
Lyle, S., Huppert, H. E., Hallworth, M., Bickle, M. & Chadwick, A. 2005 Axisymmetric gravity currents in a porous medium. J. Fluid Mech. 543, 293–302.Google Scholar
MacMinn, C. W., Neufeld, J. A., Hesse, M. & Huppert, H. E. 2012 Spreading and convective dissolution of carbon dioxide in vertically confined, horizontal aquifers. Water Resour. Res. 48, W11516,1–11.Google Scholar
Manins, P. C. 1979 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 91, 765–781.CrossRefGoogle Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Nabi, S. & Flynn, M. R. 2013 The hydraulics of exchange flow between adjacent confined building zones. Build. Environ. 59, 76–90.Google Scholar
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, M. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404,1–5.Google Scholar
Nield, D. A. & Kuznetsov, A. V. 2013 An historical and topical note on convection in porous media. J. Heat Transfer 135, 061201,1–10.Google Scholar
Poling, B. E., Prausnitz, J. M. & O’Connell, J. P. 2000 The Properties of Gases and Liquids. McGraw-Hill.Google Scholar
Roes, M. A.2014 Buoyancy-driven convection in a ventilated porous medium. Master’s thesis, University of Alberta.Google Scholar
Roes, M. A., Bolster, D. T. & Flynn, M. R. 2014 Buoyant convection from a discrete source in a leaky porous medium. J. Fluid Mech. 755, 204–229.Google Scholar
Winsauer, W. O., Shearin, H. M., Masson, P. H. & Williams, M. 1952 Resistivity of brine-saturated sands in relation to pore geometry. AAPG Bull. 36–2, 253–277.Google Scholar
Wooding, R. A. 1963 Convection in a saturated porous medium at large Rayleigh number or Péclet number. J. Fluid Mech. 15, 527–544.Google Scholar

Sahu supplementary movie

Gravity current and first front evolution for Experiment 13. The red curve shows the prediction based on the model equations of section 2. This curve is superimposed on top of the laboratory images.

Download Sahu supplementary movie(Video)
Video 420.3 KB