Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-20T16:47:57.042Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study on the effect of wall proximity on the flow around a cylinder under an axial magnetic field

Published online by Cambridge University Press:  25 November 2024

Ze-Dong Wang Open the ORCID record for Ze-Dong Wang [Opens in a new window] ,
Qi-Long Zhang ,
Yuri B. Kolesnikov ,
Ze Lyu ,
Juan-Cheng Yang ,
Ming-Jiu Ni Open the ORCID record for Ming-Jiu Ni [Opens in a new window]  and
Nian-Mei Zhang Open the ORCID record for Nian-Mei Zhang [Opens in a new window]
Ze-Dong Wang
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China
Qi-Long Zhang
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China
Yuri B. Kolesnikov
Affiliation:
Technische Universitat Ilmenau, PF 100565, 98684 Ilmenau, Germany
Ze Lyu
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China
Juan-Cheng Yang
Affiliation:
State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi'an Jiaotong University, Xi'an 710049, PR China
Ming-Jiu Ni
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China
Nian-Mei Zhang*
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China
*
† Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

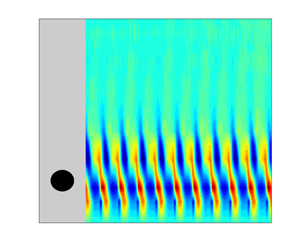
Investigations are conducted on the effect of wall proximity on the flow around a cylinder under an axial magnetic field, using the electrical potential probe technology to measure the velocity of liquid metal flow. The study focused on the impact of the inlet velocity of the fluid, the magnetic field and wall proximity on the characteristics of velocity fields, particularly on the vortex-shedding mode. Based on different magnitudes of the magnetic field and the distance from the cylinder to the duct wall, three types of vortex-shedding modes are identified, (I) shear layer oscillation state, (II) quasi-two-dimensional vortex-shedding states and (III) transition of the magnetohydrodynamic to hydrodynamic Kármán street. The transitions between these modes are analysed in detail. The experimental results show that the weak wall-proximity effect leads to the formation of the Kármán vortex street, while a reverse Kármán vortex street and secondary vortices emerge under a strong wall-proximity effect. It is noticed that the Kelvin–Helmholtz instability drives vortex shedding under regime I, leading to an increase in the Strouhal number (St) with stronger magnetic fields. Additionally, under a strong axial magnetic field, the wall-proximity effect (‘Shercliff layer effect’) promotes the instability of shear layers on both sides of the cylinder. These unique coupling effects are validated by variations in modal coefficients and energy proportions under different vortex-shedding regimes using the proper orthogonal decomposition method.

JFM classification

Vortex Flows: Vortex shedding Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A23
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abdou, M., Morley, N.B., Smolentsev, S., Ying, A., Malang, S., Rowcliffe, A. & Ulrickson, M. 2015 Blanket/first wall challenges and required R&D on the pathway to DEMO. Fusion Engng Des. 100, 2–43.CrossRefGoogle Scholar
Andreev, O. & Kolesnikov, Y.B. 1998 Experimental investigation of a flow around a conducting cylinder in an axial homogeneous magnetic field. Magnetohydrodynamics 34 (4), 286–293.Google Scholar
Bearman, P.W. & Zdravkovich, M.M. 1978 Flow around a circular cylinder near a plane boundary. J. Fluid Mech. 89 (1), 33–47.CrossRefGoogle Scholar
Belyaev, I., Sardov, P., Melnikov, I. & Frick, P. 2021 Limits of strong magneto-convective fluctuations in liquid metal flow in a heated vertical pipe affected by a transverse magnetic field. Intl J. Therm. Sci. 161, 106773.CrossRefGoogle Scholar
Belyaev, I.A., Mironov, I.S., Luchinkin, N.A., Listratov, Y.I., Kolesnikov, Y.B., Kransov, D., Zikanov, O. & Molokov, S. 2022 Experimental study of submerged liquid metal jet in a rectangular duct in a transverse magnetic field. J. Fluid Mech. 953, A10.CrossRefGoogle Scholar
Bühler, L., Mistrangelo, C. & Brinkmann, H.-J. 2020 Experimental investigation of liquid metal MHD flow entering a flow channel insert. Fusion Engng Des. 154, 111484.CrossRefGoogle Scholar
Burr, U., Barleon, L., Müller, U. & Tsinober, A. 2000 Turbulent transport of momentum and heat in magnetohydrodynamic rectangular duct flow with strong sidewall jets. J. Fluid Mech. 406, 247–279.CrossRefGoogle Scholar
Cassells, O.G.W., Hussam, W.K. & Sheard, G.J. 2016 Heat transfer enhancement using rectangular vortex promoters in confined quasi-two-dimensional magnetohydrodynamic flows. Intl J. Heat Mass Transfer 93, 186–199.CrossRefGoogle Scholar
Cassells, O.G.W., Vo, T., Pothérat, A. & Sheard, G.J. 2019 From three-dimensional to quasi-two-dimensional: transient growth in magnetohydrodynamic duct flows. J. Fluid Mech. 861, 382–406.CrossRefGoogle Scholar
Chatterjee, D. & Gupta, S.K. 2015 MHD flow and heat transfer behind a square cylinder in a duct under strong axial magnetic field. Intl J. Heat Mass Transfer 88, 1–13.CrossRefGoogle Scholar
Davidson, P.A. 1997 The role of angular momentum in the magnetic damping of turbulence. J. Fluid Mech. 336, 123–150.CrossRefGoogle Scholar
Dipankar, A. & Sengupta, T.K. 2005 Flow past a circular cylinder in the vicinity of a plane wall. J. Fluids Struct. 20 (3), 403–423.CrossRefGoogle Scholar
Dousset, V. & Pothérat, A. 2008 Numerical simulations of a cylinder wake under a strong axial magnetic field. Phys. Fluids 20 (1), 017104.CrossRefGoogle Scholar
Dousset, V. & Pothérat, A. 2012 Characterization of the flow past a truncated square cylinder in a duct under a spanwise magnetic field. J. Fluid Mech. 691, 341–367.CrossRefGoogle Scholar
Eckert, S., Cramer, A. & Gerbeth, G. 2007 Velocity measurement techniques for liquid metal flows. In Magnetohydrodynamics. Fluid Mechanics and its Applications, vol. 3, pp. 275–294. Springer.CrossRefGoogle Scholar
Frank, M., Barleon, L. & Müller, U. 2001 Visual analysis of two-dimensional magnetohydrodynamics. Phys. Fluids 13 (8), 2287–2295.CrossRefGoogle Scholar
Hamid, A.H.A., Hussam, W.K., Pothérat, A. & Sheard, G.J. 2015 Spatial evolution of a quasi-two-dimensional kármán vortex street subjected to a strong uniform magnetic field. Phys. Fluids 27 (5), 053602.CrossRefGoogle Scholar
He, G.-S. & Wang, J.-J. 2015 Flat plate boundary layer transition induced by a controlled near-wall circular cylinder wake. Phys. Fluids 27 (2), 024106.CrossRefGoogle Scholar
He, G.-S., Wang, J.-J., Pan, C., Feng, L.-H., Gao, Q. & Rinoshika, A. 2017 Vortex dynamics for flow over a circular cylinder in proximity to a wall. J. Fluid Mech. 812, 698–720.CrossRefGoogle Scholar
Hunt, J.C.R. & Ludford, G.S.S. 1968 Three-dimensional MHD duct flows with strong transverse magnetic fields. Part 1. Obstacles in a constant area channel. J. Fluid Mech. 33 (04), 693.CrossRefGoogle Scholar
Hussam, W.K., Hamid, A.H.A., Ng, Z.Y. & Sheard, G.J. 2018 Effect of vortex promoter shape on heat transfer in MHD duct flow with axial magnetic field. Intl J. Therm. Sci. 134, 453–464.CrossRefGoogle Scholar
Hussam, W.K. & Sheard, G.J. 2013 Heat transfer in a high hartmann number MHD duct flow with a circular cylinder placed near the heated side-wall. Intl J. Heat Mass Transfer 67, 944–954.CrossRefGoogle Scholar
Hussam, W.K., Thompson, M.C. & Sheard, G.J. 2011 Dynamics and heat transfer in a quasi-two-dimensional MHD flow past a circular cylinder in a duct at high Hartmann number. Intl J. Heat Mass Transfer 54 (5–6), 1091–1100.CrossRefGoogle Scholar
Hussam, W.K., Thompson, M.C. & Sheard, G.J. 2012 Optimal transient disturbances behind a circular cylinder in a quasi-two-dimensional magnetohydrodynamic duct flow. Phys. Fluids 24 (2), 024105.CrossRefGoogle Scholar
Jiang, H. & Cheng, L. 2017 Strouhal–Reynolds number relationship for flow past a circular cylinder. J. Fluid Mech. 832, 170–188.CrossRefGoogle Scholar
Kanaris, N., Albets, X., Grigoriadis, D. & Kassinos, S. 2013 Three-dimensional numerical simulations of magnetohydrodynamic flow around a confined circular cylinder under low, moderate, and strong magnetic fields. Phys. Fluids 25 (7), 074102.CrossRefGoogle Scholar
Kiya, M., Tamura, H. & Arie, M. 1980 Vortex shedding from a circular cylinder in moderate-Reynolds-number shear flow. J. Fluid Mech. 141 (4), 721–735.Google Scholar
Klein, R., Pothérat, A. & Alferenok, A. 2009 Experiment on a confined electrically driven vortex pair. Phys. Rev. E 79 (1), 016304.CrossRefGoogle ScholarPubMed
Kolesnikov, Y.B. & Tsinober, A.B. 1976 Experimental investigation of two-dimensional turbulence behind a grid. Fluid Dyn. 9 (4), 621–624.CrossRefGoogle Scholar
Kusumi, K., Kunugi, T., Yokomine, T., Kawara, Z., Wu, Y., Sagara, A. & Tanaka, T. 2019 Thermal mixing enhancement of liquid metal film-flow by various obstacles under vertical magnetic field. Fusion Engng Des. 146, 2158–2162.CrossRefGoogle Scholar
Messadek, K. & Moreau, R. 2002 An experimental investigation of MHD quasi-two-dimensional turbulent shear flows. J. Fluid Mech. 456, 137–159.CrossRefGoogle Scholar
Mistrangelo, C. & Bühler, L. 2018 Determination of multichannel MHD velocity profiles from wall-potential measurements and numerical simulations. Fusion Engng Des. 130, 137–141.CrossRefGoogle Scholar
Mistrangelo, C., Bühler, L., Alberghi, C., Bassini, S., Candido, L., Courtessole, C., Tassone, A., Urgorri, F.R. & Zikanov, O. 2021 MHD R&D activities for liquid metal blankets. Energies 14 (20), 6640.CrossRefGoogle Scholar
Moreau, R. 1990 Magnetohydrodynamics. Fluid Mechanics and its Applicaitons, vol. 3. Springer.CrossRefGoogle Scholar
Morley, N.B., Burris, J., Cadwallader, L.C. & Nornberg, M.D. 2008 Gainsn usage in the research laboratory. Rev. Sci. Instrum. 79 (5), 056107.CrossRefGoogle ScholarPubMed
Mück, B., Günther, C., Müller, U. & Bühler, L. 2000 Three-dimensional MHD flows in rectangular ducts with internal obstacles. J. Fluid Mech. 418, 265–295.CrossRefGoogle Scholar
Müller, U. & Bühler, L. 2001 Magnetofluiddynamics in Channels and Containers. Springer.CrossRefGoogle Scholar
Pan, J.-H., Zhang, N.-M. & Ni, M.-J. 2019 Wake structure of laminar flow past a sphere under the influence of a transverse magnetic field. J. Fluid Mech. 873, 151–173.CrossRefGoogle Scholar
Pothérat, A. 2007 Quasi-two-dimensional perturbations in duct flows under transverse magnetic field. Phys. Fluids 19 (7), 074104.CrossRefGoogle Scholar
Pothérat, A. & Klein, R. 2014 Why, how and when MHD turbulence at low becomes three-dimensional. J. Fluid Mech. 761, 168–205.CrossRefGoogle Scholar
Rhoads, J.R., Edlund, E.M. & Ji, H. 2014 Effects of magnetic field on the turbulent wake of a cylinder in free-surface magnetohydrodynamic channel flow. J. Fluid Mech. 742, 446–465.CrossRefGoogle Scholar
Smolentsev, S. 2023 Modeling of transport processes in liquid-metal fusion blankets: past, present, and future. Fusion Sci. Technol. 79 (3), 251–273.CrossRefGoogle Scholar
Smolentsev, S., Morley, N.B., Abdou, M.A. & Malang, S. 2015 Dual-coolant lead–lithium (DCLL) blanket status and R&D needs. Fusion Engng Des. 100, 44–54.CrossRefGoogle Scholar
Sommeria, J. & Moreau, R. 1982 Why, how, and when, MHD turbulence becomes two-dimensional. J. Fluid Mech. 118 (1), 507.CrossRefGoogle Scholar
Sreenivasan, B. & Alboussière, T. 2002 Experimental study of a vortex in a magnetic field. J. Fluid Mech. 464, 287–309.CrossRefGoogle Scholar
Thompson, M.C., Leweke, T. & Hourigan, K. 2021 Bluff bodies and wake–wall interactions. Annu. Rev. Fluid Mech. 53 (1), 347–376.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar
Zdravkovich, M.M. 1997 Flow Around Circular Cylinder Vol 1: Fundamentals. Oxford University Press.CrossRefGoogle Scholar
Zhang, X.-F., Yang, J.-C., Ni, M.-J., Zhang, N.-M. & Yu, X.-G. 2023 Numerical simulations of flow around dual tandem circular cylinders under a strong axial magnetic field. Phys. Fluids 35 (2), 023604.CrossRefGoogle Scholar
Zhou, J., Qiu, X., Li, J. & Liu, Y. 2021 The gap ratio effect on evolution behind a cylinder placed near a wall. Phys. Fluids 33 (3), 037112.CrossRefGoogle Scholar
Zovatto, L. & Pedrizzetti, G. 2001 Flow about a circular cylinder between parallel walls. J. Fluid Mech. 440, 1–25.CrossRefGoogle Scholar