Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T01:17:26.993Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study of turbulent bubbly jet. Part 1. Simultaneous measurement of three-dimensional velocity fields of bubbles and water

Published online by Cambridge University Press:  04 May 2022

Dong Kim Open the ORCID record for Dong Kim [Opens in a new window] ,
Daniel Schanz Open the ORCID record for Daniel Schanz [Opens in a new window] ,
Matteo Novara Open the ORCID record for Matteo Novara [Opens in a new window] ,
Hyunduk Seo Open the ORCID record for Hyunduk Seo [Opens in a new window] ,
Youngwoo Kim ,
Andreas Schröder Open the ORCID record for Andreas Schröder [Opens in a new window]  and
Kyung Chun Kim Open the ORCID record for Kyung Chun Kim [Opens in a new window]
Dong Kim
Affiliation:
School of Mechanical Engineering, University of Ulsan, Ulsan 44610, Republic of Korea
Daniel Schanz
Affiliation:
Institute of Aerodynamics and Flow Technology, German Aerospace Center (DLR), 37073 Göttingen, Germany
Matteo Novara
Affiliation:
Institute of Aerodynamics and Flow Technology, German Aerospace Center (DLR), 37073 Göttingen, Germany
Hyunduk Seo
Affiliation:
School of Mechanical Engineering, Pusan National University, Busan 46241, Republic of Korea
Youngwoo Kim
Affiliation:
School of Mechanical Engineering, Pusan National University, Busan 46241, Republic of Korea
Andreas Schröder
Affiliation:
Institute of Aerodynamics and Flow Technology, German Aerospace Center (DLR), 37073 Göttingen, Germany
Kyung Chun Kim*
Affiliation:
School of Mechanical Engineering, Pusan National University, Busan 46241, Republic of Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

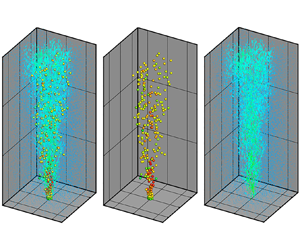
This study proposes a method for simultaneous measurements of time-resolved three-dimensional velocity fields of the dispersed and continuous phases of a turbulent bubbly jet at a low void fraction using Lagrangian particle tracking (LPT) velocimetry with the Shake-The-Box algorithm. Four high-speed cameras are used to acquire time series of images that include both bubbles and fluid tracer particles. Bubbles are firstly tracked using intensity differences between tracer particles and bubbles, then the bubble images are removed from the camera images and all tracer particles are tracked using the residual images. Subsequently, FlowFit interpolation is applied to the LPT results obtained by phase separation to investigate flow characteristics of a bubbly jet. The bubbly jet was divided into two regions along the vertical direction: jet-like and plume-like regions. Streamwise vortex structures of continuous phase were generated mainly by the rising bubbles. The Gaussian and top-hat velocity profiles matched well with the ensemble-averaged fluid and bubble velocities, respectively. The measured slip velocity in the radial direction was not constant but linearly increased. The classical assumption of self-similarity with Gaussian profiles for fluid velocity and bubble concentration is experimentally verified. The fluid volume flux and entrainment coefficient are obtained as a function of the slip velocity, void fraction, plume and bubble width based on three-dimensional measurements. We found that the classical integral theory agrees well with experiments in the plume region.

JFM classification

Multiphase and Particle-laden Flows: Gas/liquid flow Wakes/Jets: Jets Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 941 , 25 June 2022 , A42
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aliyu, A.M., Almabrok, A.A., Baba, Y.D., Archibong, A.-E., Lao, L., Yeung, H. & Kim, K.C. 2017 Prediction of entrained droplet fraction in co-current annular gas–liquid flow in vertical pipes. Exp. Therm. Fluid Sci. 85, 287–304.CrossRefGoogle Scholar
Aliyu, A.M., Seo, H., Kim, M. & Kim, K.C. 2018 An experimental study on the characteristics of ejector-generated bubble swarms. J. Vis. 21, 711–728.CrossRefGoogle Scholar
Ansari, S. & Nobes, D.S. 2020 Interaction of loosely packed bubbly flow passing through a pore space. J. Vis. 23, 649–660.CrossRefGoogle Scholar
Asaeda, T. & Imberger, J. 1993 Structure of bubble plumes in linearly stratified environments. J. Fluid Mech. 249, 35–57.CrossRefGoogle Scholar
Balachandar, S. & Eaton, J.K. 1993 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.CrossRefGoogle Scholar
Besagni, G., Guédon, G.R. & Inzoli, F. 2015 Annular gap bubble column: experimental investigation and computational fluid dynamics modeling. Trans. ASME J. Fluids Engng 138, 011302.CrossRefGoogle Scholar
Besagni, G. & Inzoli, F. 2017 The effect of liquid phase properties on bubble column fluid dynamics: gas holdup, flow regime transition, bubble size distributions and shapes, interfacial areas and foaming phenomena. Chem. Engng Sci. 170, 270–296.CrossRefGoogle Scholar
Bombardelli, F.A., Buscaglia, G.C., Rehmann, C.R., Rincón, L.E. & García, M.H. 2007 Modeling and scaling of aeration bubble plumes: a two-phase flow analysis. J. Hydraul Res. 45, 617–630.CrossRefGoogle Scholar
Brevik, I. 1977 Two-dimensional air-bubble plume. J. Waterways Port Coast. Ocean Engng 103, 101–115.CrossRefGoogle Scholar
Brücker, C. 2000 PIV in Two-phase Flows, 1. Von Kármán Institute for Fluid Dynamics, Lecture Series.Google Scholar
Caulfield, J.A., Adams, E.E., Auerbach, D.I. & Herzog, H.J. 1997 Impacts of ocean CO$_{2}$ disposal on marine life. II. Probabilistic plume exposure model used with a time-varying dose-response analysis. Environ. Model. Assess. 24, 345–353.CrossRefGoogle Scholar
Clift, R., Grace, J.R. & Weber, M.E. 1978 Bubbles, Drops, and Particles. Academic Press.Google Scholar
Cramers, P.H.M.R. & Beenackers, A.A.C.M. 2001 Influence of the ejector configuration, scale and the gas density on the mass transfer characteristics of gas-liquid ejectors. Chem. Engng J. 82, 131–141.CrossRefGoogle Scholar
Crapper, P.F. 1977 Forced plume characteristics. Tellus 29, 470–475.CrossRefGoogle Scholar
Davies, P.O.A.L., Fisher, M.J. & Barratt, M.J. 1963 The characteristics of the turbulence in the mixing region of a round jet. J. Fluid Mech. 15, 337–367.CrossRefGoogle Scholar
Deen, N. 2001 An experimental and computational study of fluid dynamics in gas-liquid chemical reactors. PhD thesis, Aalborg University, Esbjerg.Google Scholar
Deen, N., Westerweel, J. & Delnoij, E. 2002 Two-phase PIV in bubbly flows: status and trends. Chem. Engng Technol. 251, 97–101.3.0.CO;2-7>CrossRefGoogle Scholar
Delnoij, E., Westerweel, J., Deen, N., Kuipers, J. & van Swaaij, W. 1999 Ensemble correlation PIV applied to bubble plumes rising in a bubble column. Chem. Engng Sci. 5421, 5159–5171.CrossRefGoogle Scholar
Ditmars, J.D. & Cederwall, K. 1975 Analysis of air-bubble plumes, In Coastal Engineering 1974, pp. 2209–2226.Google Scholar
Echeverría, C., Porta, D., Stern, C. & Guzmán, J.E.V. 2020 A method to determine the measurement volume for particle shadow tracking velocimetry (PSTV). J. Vis. 23, 577–590.CrossRefGoogle Scholar
Ehlers, F., Schröder, A. & Gesemann, S. 2020 Enforcing temporal consistency in physically constrained flow field reconstruction with FlowFit by use of virtual tracer particles. Meas. Sci. Technol. 31, 094013.CrossRefGoogle Scholar
Evans, J.T. 1955 Pneumatic and similar breakwaters. Proc. R. Soc. Lond. A 231, 457–466.Google Scholar
Fannelop, T.K. & Sjoen, K. 1980 Hydrodynamics of underwater blowouts. In Proc. AIAA 18th Aerospace Sci. Meeting, AIAA Papers 1980-219.Google Scholar
Fisher, H.B., List, J.E., Koh, C.R., Imberger, J. & Brooks, N.H. 1979 Mixing in Inland and Coastal Waters. Academic Press.Google Scholar
Fraga, B., Stoesser, T., Lai, C.C.K. & Socolofsky, S.A. 2016 A LES-based Eulerian-Lagrangian approach to predict the dynamics of bubble plumes. Ocean Model. 97, 27–36.CrossRefGoogle Scholar
Fujiwara, A., Minato, D. & Hishida, K. 2004 Effect of bubble diameter on modification of turbulence in an upward pipe flow. Intl J. Heat Fluid Flow 25, 481–488.CrossRefGoogle Scholar
Gesemann, S. 2021 TrackFit: uncertainty quantification, optimal filtering and interpolation of tracks for time-resolved Lagrangian particle tracking. In 14th International Symposium on Particle Image Velocimetry.CrossRefGoogle Scholar
Gesemann, S., Huhn, F., Schanz, D. & Schröder, A. 2016 From noisy particle tracks to velocity, acceleration and pressure fields using B-splines and penalties. In 18th International Symposium on Applications of Laser and Imaging Techniques to Fluid Mechanics, pp. 4–7.Google Scholar
Groen, J.S., Mudde, R.F. & Van Den Akker, H.E.A. 1999 On the application of LDA to bubbly flow in the wobbling regime. Exp. Fluids 27, 435–449.CrossRefGoogle Scholar
Grota, B. & Strauß, K. 2000 DPIV in a particle-laden gas flow-the influence of the particle fluctuation velocities on the accuracy of several cross-correlation-based analysis methods. In Proc. EUROMECH 4.Google Scholar
Gui, L., Lindken, R. & Merzkirch, W. 1997 Phase-separated PIV measurements of the flow around systems of bubbles rising in water. In ASME Fluids Engng Division Summer Meeting, vol. 97, pp. 22–26.Google Scholar
Gui, L. & Merzkirch, W. 1996 A method of tracking ensembles of particle images. Exp. Fluids 216, 465–468.CrossRefGoogle Scholar
Henderson-Sellers, B. 1983 The zone of flow establishment for plumes with significant buoyancy. Appl. Math. Model. 7, 395–398.CrossRefGoogle Scholar
Hessenkemper, H., Ziegenhein, T., Rzehak, R., Lucas, D. & Tomiyama, A. 2021 Lift force coefficient of ellipsoidal single bubbles in water. Intl J. Multiphase Flow 138, 103587.CrossRefGoogle Scholar
van Hout, R., Murugan, S., Mitra, A. & Cukurel, B. 2021 Coaxial circular jets. A review. Fluids 6, 147.CrossRefGoogle Scholar
Hugi, C. 1993 Modelluntersuchungen von blasenstrahlen für die seebelüftung. PhD thesis, ETH, Zürich.Google Scholar
Hunt, G.R. & Kaye, N.G. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.CrossRefGoogle Scholar
Jahn, T., Schanz, D. & Schröder, A. 2021 Advanced iterative particle reconstruction for Lagrangian particle tracking. Exp. Fluids 62, 179.CrossRefGoogle Scholar
Kiger, K. & Pan, C. 2000 PIV technique for the simultaneous measurement of dilute two-phase flows. J. Fluids Engng 1224, 811–818.CrossRefGoogle Scholar
Lai, A.C.H., Chan, S.N., Law, A.W.-K. & Adams, E.E. 2016 Spreading hypothesis of a particle plume. J. Hydraul. Engng ASCE 142, 04016065.CrossRefGoogle Scholar
Lai, C.C.K. & Socolofsky, S.A. 2019 The turbulent kinetic energy budget in a bubble plume. J. Fluid Mech. 865, 993–1041.CrossRefGoogle Scholar
Lemckert, C.J. & Imberger, J. 1993 Energetic bubble plumes in arbitrary stratification. J. Hydraul. Engng ASCE 1196, 680–703.CrossRefGoogle Scholar
Li, G., Wang, B., Wu, H. & DiMarco, S.F. 2020 Impact of bubble size on the integral characteristics of bubble plumes in quiescent and unstratified water. Intl J. Multiphase Flow 125, 103230.CrossRefGoogle Scholar
Lima Neto, I.E., Zhu, D.Z. & Rajaratnam, N. 2008 Bubbly jets in stagnant water. Intl J. Multiphase Flow 34, 1130–1141.CrossRefGoogle Scholar
Lindken, R., Gui, L. & Merzkirch, W. 1999 Velocity measurements in multiphase flow by means of particle image velocimetry. Chem. Engng Technol. 223, 202–206.3.0.CO;2-K>CrossRefGoogle Scholar
Lindken, R. & Merzkirch, W. 2002 A novel PIV technique for measurements in multiphase flows and its application to two-phase bubbly flows. Exp. Fluids 336, 814–825.CrossRefGoogle Scholar
Masuk, A., Salibindla, A. & Ni, R. 2021 The orientational dynamics of deformable finite-sized bubbles in turbulence. J. Fluid Mech. 915, A79.CrossRefGoogle Scholar
Mathai, V., Lohse, D. & Sun, C. 2020 Bubbly and buoyant particle–laden turbulent flows. Annu. Rev. Condens. Matter Phys. 11, 529–559.CrossRefGoogle Scholar
McDougall, T.J. 1978 Bubble plumes in stratified environments. J. Fluid Mech. 854, 655–672.CrossRefGoogle Scholar
Milgram, J.H. 1983 Mean flow in round bubble plumes. J. Fluid Mech. 133, 345–376.CrossRefGoogle Scholar
Milgram, J.H. & Van Houten, R.J. 1982 Plumes from sub-sea well blowouts. In Proceedings of 3rd International Conference on BOSS 1, pp. 659–684.Google Scholar
Morton, B.R. 1959 Forced plumes. J. Fluid Mech. 5, 151–163.CrossRefGoogle Scholar
Morton, B.R., Taylor, G. & Turner, J.S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. A 234, 1–23.Google Scholar
Motarjemi, M. & Jameson, G. 1978 Mass transfer from very small bubbles-the optimum bubble size for aeration. Chem. Engng Sci. 3311, 1415–1423.CrossRefGoogle Scholar
Muilwijk, C. & Van den Akker, H.E.A. 2019 Experimental investigation on the bubble formation from needles with and without liquid co-flow. Chem. Engng Sci. 202, 318–335.CrossRefGoogle Scholar
Priestley, C.H.B. & Ball, F.K. 1955 Continuous convection from an isolated source of heat. Q. J. R. Meteorol. Soc. 81, 144–157.CrossRefGoogle Scholar
Risso, F. 2018 Agitation, mixing, and transfers induced by bubbles. Annu. Rev. Fluid Mech. 50, 25–48.CrossRefGoogle Scholar
Saini, S. & Banerjee, J. 2021 Physics of aeration in slug: flow visualization analysis in horizontal pipes. J. Vis. 24, 917–930.CrossRefGoogle Scholar
Sakakibara, J., Wicker, R. & Eaton, J. 1996 Measurements of particle-fluid velocity correlation and the extra dissipation in a round jet. Intl J. Multiphase Flow 225, 863–881.CrossRefGoogle Scholar
Schanz, D., Gesemann, S. & Schröder, A. 2016 Shake-the-box: Lagrangian particle tracking at high particle image densities. Exp. Fluids 57, 70.CrossRefGoogle Scholar
Schanz, D., Gesemann, S., Schröder, A., Wieneke, B. & Novara, M. 2012 Non-uniform optical transfer functions in particle imaging: calibration and application to tomographic reconstruction. Meas. Sci. Technol. 24, 024009.CrossRefGoogle Scholar
Schanz, D., Novara, M. & Schröder, A. 2021 Shake-The-Box particle tracking with variable time-steps in flows with high velocity range (VT-STB). In 14th International Symposium on Particle Image Velocimetry (ISPIV 2021).CrossRefGoogle Scholar
Schröder, A., Schanz, D., Michaelis, D., Cierpka, C., Scharnowski, S. & Kähler, C.J. 2015 Advances of PIV and 4D-PTV” shake-the-box” for turbulent flow analysis–the flow over periodic hills. Flow Turbul. Combust. 95, 193–209.CrossRefGoogle Scholar
Sciacchitano, A., Leclaire, B. & Schröder, A. 2021 Main results of the first data assimilation challenge. In Proc. of 14th ISPIV, vol. 1, pp. 1–13.Google Scholar
Seo, H., Aliyu, A.M. & Kim, K.C. 2018 Enhancement of momentum transfer of bubble swarms using an ejector with water injection. Energy 162, 892–909.CrossRefGoogle Scholar
Seo, H. & Kim, K.C. 2021 Experimental study on flow and turbulence characteristics of bubbly jet with low void fraction. Intl J. Multiphase Flow 142, 103738.CrossRefGoogle Scholar
Seo, H., Marjanovic, G., Balachandar, S. & Kim, K.C. 2022 Influence of slip velocity in a two-phase bubbly jet. J. Fluid Mech. 935, A4.CrossRefGoogle Scholar
Seol, D., Bhaumik, T., Bergmann, C. & Socolofsky, S. 2007 Particle image velocimetry measurements of the mean flow characteristics in a bubble plume. J. Engng Mech. 133, 665–676.Google Scholar
Siddiqui, M.I., Munir, S., Heikal, M.R., de Sercey, G., Aziz, A.R.A. & Dass, S.C. 2016 Simultaneous velocity measurements and the coupling effect of the liquid and gas phases in slug flow using PIV–LIF technique. J. Vis. 19, 103–114.CrossRefGoogle Scholar
Socolofsky, S.A. & Adams, E.E. 2002 Multi-phase plumes in uniform and stratified cross-flow. J. Hydraul Res. 406, 661–672.CrossRefGoogle Scholar
Socolofsky, S.A. & Adams, E.E. 2003 Liquid volume fluxes in stratified multiphase plumes. J. Hydraul. Engng ASCE 12911, 905–914.CrossRefGoogle Scholar
Socolofsky, S.A. & Adams, E.E. 2005 Role of slip velocity in the behavior of stratified multiphase plumes. J. Hydraul. Engng ASCE 1314, 273–282.CrossRefGoogle Scholar
Socolofsky, S.A., Bhaumik, T. & Seol, D.-G. 2008 Double-plume integral models for near-field mixing in multiphase plumes. J. Hydraul. Engng ASCE 134, 772–783.CrossRefGoogle Scholar
Sun, T.Y. & Faeth, G.M. 1986 Structure of turbulent bubbly jets-I. Methods and centerline properties. Intl J. Multiphase Flow 12, 99–114.CrossRefGoogle Scholar
Taylor, G.I. 1955 The action of a surface current used as a breakwater. Proc. R. Soc. Lond. A 231, 466–478.Google Scholar
Terasaka, K., Hirabayashi, A., Nishino, T., Fujioka, S. & Kobayashi, D. 2011 Development of microbubble aerator for waste water treatment using aerobic activated sludge. Chem. Engng. Sci. 66, 3172–3179.CrossRefGoogle Scholar
Turner, J.S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.CrossRefGoogle Scholar
Wang, B., Lai, C.C.K. & Socolofsky, S.A. 2019 Mean velocity, spreading and entrainment characteristics of weak bubble plumes in unstratified and stationary water. J. Fluid Mech. 874, 102–130.CrossRefGoogle Scholar
Wang, B. & Socolofsky, S.A. 2015 On the bubble rise velocity of a continually released bubble chain in still water and with crossflow. Phys. Fluids 27, 103301.CrossRefGoogle Scholar
Wang, H. & Law, A.W.K. 2002 Second-order integral model for a round turbulent buoyant jet. J. Fluid Mech. 459, 397–428.CrossRefGoogle Scholar
Wieneke, B. 2008 Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 45, 549–556.CrossRefGoogle Scholar
Wieneke, B. 2012 Iterative reconstruction of volumetric particle distribution. Meas. Sci. Technol. 24, 024008.CrossRefGoogle Scholar
Wüest, A., Brooks, N.H. & Imboden, D.M. 1992 Bubble plume modeling for lake restoration. Water Resour. Res. 2812, 3235–3250.CrossRefGoogle Scholar
Xu, Y., Aliyu, A.M., Seo, H., Wang, J.J. & Kim, K.C. 2018 Effect of crossflow velocity on underwater bubble swarms. Intl J. Multiphase Flow 105, 60–73.CrossRefGoogle Scholar
Yang, D., Chen, B.C., Socolofsky, S.A., Chamecki, M. & Meneveau, C. 2016 Large-eddy simulation and parameterization of buoyant plume dynamics in stratified flow. J. Fluid Mech. 794, 798–833.CrossRefGoogle Scholar
Yapa, P.D., Zheng, L. & Nakata, K. 1999 Modeling underwater oil/gas jets and plumes. J. Hydraul. Engng ASCE 1255, 481–491.CrossRefGoogle Scholar
Zheng, S.Q., Yao, Y., Guo, F.F., Bi, R.S. & Li, J.Y. 2010 Local bubble size distribution, gas-liquid interfacial areas and gas holdups in an up-flow ejector. Chem. Engng Sci. 65, 5264–5271.CrossRefGoogle Scholar
Ziegenhein, T., Zalucky, J., Rzehak, R. & Lucas, D. 2016 On the hydrodynamics of airlift reactors. Part 1. Experiments. Chem. Engng Sci. 150, 54–65.CrossRefGoogle Scholar

Kim et al. Supplementary Movie 1

Lagrangian bubble-particle tracking and phase separation results.

Download Kim et al. Supplementary Movie 1(Video)
Video 18.4 MB

Kim et al. Supplementary Movie 2

Instantaneous velocity field of bubble and liquid phase by FlowFit interpolation.

Download Kim et al. Supplementary Movie 2(Video)
Video 13.9 MB