Article contents
Experimental study of rotating-disk boundary-layer flow with surface roughness
Published online by Cambridge University Press: 24 November 2015
Abstract
Rotating-disk boundary-layer flow is known to be locally absolutely unstable at 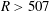 $R>507$ as shown by Lingwood (J. Fluid Mech., vol. 299, 1995, pp. 17–33) and, for the clean-disk condition, experimental observations show that the onset of transition is highly reproducible at that Reynolds number. However, experiments also show convectively unstable stationary vortices due to cross-flow instability triggered by unavoidable surface roughness of the disk. We show that if the surface is sufficiently rough, laminar–turbulent transition can occur via a convectively unstable route ahead of the onset of absolute instability. In the present work we compare the laminar–turbulent transition processes with and without artificial surface roughnesses. The differences are clearly captured in the spectra of velocity time series. With the artificial surface roughness elements, the stationary-disturbance component is dominant in the spectra, whereas both stationary and travelling components are represented in spectra for the clean-disk condition. The wall-normal profile of the disturbance velocity for the travelling mode observed for a clean disk is in excellent agreement with the critical absolute instability eigenfunction from local theory; the wall-normal stationary-disturbance profile, by contrast, is distinct and the experimentally measured profile matches the stationary convective instability eigenfunction. The results from the clean-disk condition are compared with theoretical studies of global behaviours in spatially developing flow and found to be in good qualitative agreement. The details of stationary disturbances are also discussed and it is shown that the radial growth rate is in excellent agreement with linear stability theory. Finally, large stationary structures in the breakdown region are described.
$R>507$ as shown by Lingwood (J. Fluid Mech., vol. 299, 1995, pp. 17–33) and, for the clean-disk condition, experimental observations show that the onset of transition is highly reproducible at that Reynolds number. However, experiments also show convectively unstable stationary vortices due to cross-flow instability triggered by unavoidable surface roughness of the disk. We show that if the surface is sufficiently rough, laminar–turbulent transition can occur via a convectively unstable route ahead of the onset of absolute instability. In the present work we compare the laminar–turbulent transition processes with and without artificial surface roughnesses. The differences are clearly captured in the spectra of velocity time series. With the artificial surface roughness elements, the stationary-disturbance component is dominant in the spectra, whereas both stationary and travelling components are represented in spectra for the clean-disk condition. The wall-normal profile of the disturbance velocity for the travelling mode observed for a clean disk is in excellent agreement with the critical absolute instability eigenfunction from local theory; the wall-normal stationary-disturbance profile, by contrast, is distinct and the experimentally measured profile matches the stationary convective instability eigenfunction. The results from the clean-disk condition are compared with theoretical studies of global behaviours in spatially developing flow and found to be in good qualitative agreement. The details of stationary disturbances are also discussed and it is shown that the radial growth rate is in excellent agreement with linear stability theory. Finally, large stationary structures in the breakdown region are described.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 24
- Cited by



