Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T17:31:23.491Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study of inertial particles clustering and settling in homogeneous turbulence

Published online by Cambridge University Press:  14 February 2019

Alec J. Petersen Open the ORCID record for Alec J. Petersen [Opens in a new window] ,
Lucia Baker Open the ORCID record for Lucia Baker [Opens in a new window]  and
Filippo Coletti
Alec J. Petersen*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55414, USA St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA
Lucia Baker
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55414, USA St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA
Filippo Coletti
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55414, USA St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study experimentally the spatial distribution, settling and interaction of sub-Kolmogorov inertial particles with homogeneous turbulence. Utilizing a zero-mean-flow air turbulence chamber, we drop size-selected solid particles and study their dynamics with particle imaging and tracking velocimetry at multiple resolutions. The carrier flow is simultaneously measured by particle image velocimetry of suspended tracers, allowing the characterization of the interplay between both the dispersed and continuous phases. The turbulence Reynolds number based on the Taylor microscale ranges from 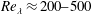$Re_{\unicode[STIX]{x1D706}}\approx 200{-}500$, while the particle Stokes number based on the Kolmogorov scale varies between 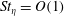$St_{\unicode[STIX]{x1D702}}=O(1)$ and 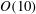$O(10)$. Clustering is confirmed to be most intense for 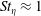$St_{\unicode[STIX]{x1D702}}\approx 1$, but it extends over larger scales for heavier particles. Individual clusters form a hierarchy of self-similar, fractal-like objects, preferentially aligned with gravity and with sizes that can reach the integral scale of the turbulence. Remarkably, the settling velocity of 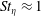$St_{\unicode[STIX]{x1D702}}\approx 1$ particles can be several times larger than the still-air terminal velocity, and the clusters can fall even faster. This is caused by downward fluid fluctuations preferentially sweeping the particles, and we propose that this mechanism is influenced by both large and small scales of the turbulence. The particle–fluid slip velocities show large variance, and both the instantaneous particle Reynolds number and drag coefficient can greatly differ from their nominal values. Finally, for sufficient loadings, the particles generally augment the small-scale fluid velocity fluctuations, which however may account for a limited fraction of the turbulent kinetic energy.

JFM classification

Turbulent Flows: Homogeneous turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 925 - 970
Check for updates
Copyright
© Cambridge University Press 2019. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliseda, A., Cartellier, A., Hainux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.Google Scholar
Ayyalasomayajula, S., Gylfason, A., Collins, L. R., Bodenschatz, E. & Warhaft, Z. 2006 Lagrangian measurements of inertial particle accelerations in grid generated wind tunnel turbulence. Phys. Rev. Lett. 97 (14), 144507.Google Scholar
Bagchi, P. & Balachandar, S. 2003 Effect of turbulence on the drag and lift of a particle. Phys. Fluids 15 (11), 3496–3513.Google Scholar
Baker, L., Frankel, A., Mani, A. & Coletti, F. 2017 Coherent clusters of inertial particles in homogeneous turbulence. J. Fluid Mech. 833, 364–398.Google Scholar
Balachandar, S. 2009 A scaling analysis for point particle approaches to turbulent multiphase flows. Intl J. Multiphase Flow 35 (9), 801–810.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42 (1), 111–133.Google Scholar
Bateson, C. P. & Aliseda, A. 2012 Wind tunnel measurements of the preferential concentration of inertial droplets in homogeneous isotropic turbulence. Exp. Fluids 52 (6), 1373–1387.Google Scholar
Bec, J. 2003 Fractal clustering of inertial particles in random flows. Phys. Fluids 15, L81.Google Scholar
Bec, J., Biferale, L., Boffetta, G., Celani, A., Lanotte, A., Musaccio, S. & Toschi, F. 2006 Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550, 349–358.Google Scholar
Bec, J., Biferale, L., Cencini, M. & Lanotte, A. S. 2010 Intermittency in the velocity distribution of heavy particles in turbulence. J. Fluid Mech. 646, 527–536.Google Scholar
Bec, J., Biferale, L., Cencini, M., Lanotte, A., Masucchio, S. & Toschi, F. 2007 Heavy particle concentration in turbulence at dissipative and inertial scales. Phys. Rev. Lett. 98, 084502.Google Scholar
Bec, J., Cencini, M., Hillerbrand, R. & Turitsyn, K. 2008 Stochastic suspensions of heavy particles. Physica D 237, 2037–2050.Google Scholar
Bec, J., Homann, H. & Ray, S. S. 2014a Gravity-driven enhancement of heavy particle clustering in turbulent flow. Phys. Rev. Lett. 112 (18), 184501.Google Scholar
Bec, J., Homann, H. & Ray, S. S. 2014b Gravity-driven enhancement of heavy particle clustering in turbulent flow. Phys. Rev. Lett. 112, 184501.Google Scholar
Bellani, G., Byron, M. L., Collignon, A. G., Meyer, C. R. & Variano, E. A. 2012 Shape effects on turbulent modulation by large nearly neutrally buoyant particles. J. Fluid Mech. 712, 41–60.Google Scholar
Bellani, G. & Variano, E. A. 2014 Homogeneity and isotropy in a laboratory turbulent flow. Exp. Fluids 55 (1), 1646.Google Scholar
Bendat, J. S. & Piersol, A. G. 2011 Random Data Analysis and Measurement Procedures. Wiley.Google Scholar
Bewley, G. P., Saw, E.-W. & Bodenschatz, E. 2013 Observation of the sling effect. New J. Phys. 15, 083051.Google Scholar
Boivin, M., Simonin, O. & Squires, K. D. 1998 Direct numerical simulation of turbulence modulation by particles in isotropic turbulence. J. Fluid Mech. 375, 235–263.Google Scholar
Bordás, R., Roloff, Ch., Thévenin, D. & Shaw, R. A. 2013 Experimental determination of droplet collision rates in turbulence. New J. Phys. 15 (4), 045010.Google Scholar
Bosse, T. & Kleiser, L. 2006 Small particles in homogeneous turbulence: settling velocity enhancement by two-way coupling. Phys. Fluids 18, 027102.Google Scholar
Bragg, A. B. & Collins, L. R. 2014 New insights from comparing statistical theories for inertial particles in turbulence: I. Spatial distribution of particles. New J. Phys. 16, 055013.Google Scholar
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2015 Mechanisms for the clustering of inertial particles in the inertial range of isotropic turbulence. Phys. Rev. E 92 (2), 023029.Google Scholar
Calzavarini, E., Kerscher, M., Lohse, D. & Toschi, F. 2008 Dimensionality and morphology of particle and bubble clusters in turbulent flow. J. Fluid Mech. 607, 13–24.Google Scholar
Carter, D. W. & Coletti, F. 2017 Scale-to-scale anisotropy in homogeneous turbulence. J. Fluid Mech. 827, 250–284.Google Scholar
Carter, D. & Coletti, F. 2018 Small-scale structure and energy transfer in homogeneous turbulence. J. Fluid Mech. 854, 505–543.Google Scholar
Carter, D., Petersen, A., Amili, O. & Coletti, F. 2016 Generating and controlling homogeneous air turbulence using random jet arrays. Exp. Fluids 57 (12), 189.Google Scholar
Cencini, M., Bec, J., Biferale, L., Celani, A., Lanotte, A. S., Musacchio, S. & Toschi, F. 2006 Dynamics and statistics of heavy particles in turbulent flows. J. Turbul. 7, N36.Google Scholar
Chen, L., Goto, S. & Vassilicos, J. C. 2006 Turbulent clustering of stagnation points and inertial particles. J. Fluid Mech. 553, 143–154.Google Scholar
Chun, J., Koch, D. L., Rani, S. L., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.Google Scholar
Cisse, M., Homann, H. & Bec, J. 2013 Slipping motion of large neutrally buoyant particles in turbulence. J. Fluid Mech. 735, R1.Google Scholar
Clift, R., Grace, J. & Weber, M. E. 2005 Bubbles, Drops and Particles. Dover.Google Scholar
Coleman, S. W. & Vassilicos, J. C. 2009 A unified sweep-stick mechanism to explain particle clustering in two- and three-dimensional homogeneous, isotropic turbulence. Phys. Fluids 21, 113301.Google Scholar
Coletti, F., Toloui, M., Fong, K. O., Nemes, A. & Baker, L. 2016 Volumetric distribution and velocity of inertial particles in a turbulent channel flow. In 18th International Symposium on Application of Laser and Imaging Techniques to Fluid Mechanics, Lisbon, Portugal.Google Scholar
Csanady, G. T. 1963 Turbulent diffusion of heavy particles in the atmosphere. J. Atmos. Sci. 20 (3), 201–208.Google Scholar
Dávila, J. & Hunt, J. C. R. 2001 Settling of small particles near vortices and in turbulence. J. Fluid Mech. 440, 117–145.Google Scholar
Dejoan, A. & Monchaux, R. 2013 Preferential concentration and settling of heavy particles in homogeneous turbulence. Phys. Fluids 25 (1), 013301.Google Scholar
Eaton, J. K. 2009 Two-way coupled turbulence simulations of gas-particle flows using point-particle tracking. Intl J. Multiphase Flow 35 (9), 792–800.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20 (1), 169–209.Google Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52 (4), 309–329.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1992 Direct simulation of particle dispersion in decaying isotropic turbulence. J. Fluid Mech. 242, 655–700.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1993 On the two way interaction between homogeneous turbulence and dispersed solid particles. I. Turbulence modification. Phys. Fluids A 5 (7), 1790–1801.Google Scholar
Esmaily-Moghadam, M. & Mani, A. 2016 Analysis of the clustering of inertial particles in turbulent flows. Phys. Rev. Fluids 1, 084202.Google Scholar
Falconer, K. 2003 Fractal Geometry Mathematical Foundations and Applications. Wiley.Google Scholar
Falkovich, G., Fouxon, A. & Stepanov, M. G. 2002 Acceleration of rain initiation by cloud turbulence. Nature 419, 151–154.Google Scholar
Ferenc, J.-S. & Néda, Z. 2007 On the size distribution of Poisson Voronoï cells. Physica A 385 (2), 518–526.Google Scholar
Ferrante, A. & Elghobashi, S. 2003 On the physical mechanisms of two-way coupling in particle-laden isotropic turbulence. Phys. Fluids 15 (2), 315–329.Google Scholar
Fessler, J. R., Kulick, J. D. & Eaton, J. K. 1994 Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 6, 3742.Google Scholar
Fiscaletti, D., Westerweel, J. & Elsinga, G. E. 2014 Long-range 𝜇PIV to resolve the small scales in a jet at high Reynolds number. Exp. Fluids 55, 1812.Google Scholar
Fornari, W., Picano, F. & Brandt, L. 2016 Sedimentation of finite-size spheres in quiescent and turbulent environments. J. Fluid Mech. 788, 640–669.Google Scholar
Frankel, A., Pouransari, H., Coletti, F. & Mani, A. 2016 Settling of heated particles in homogeneous turbulence. J. Fluid Mech. 792, 869–893.Google Scholar
Gao, H., Li, H. & Wang, L.-P. 2013 Lattice Boltzmann simulation of turbulent flow laden with finite-size particles. Comput. Maths Applics. 65 (2), 194–210.Google Scholar
Garrett, T. J. & Yuter, S. E. 2014 Observed influence of riming, temperature, and turbulence on the fallspeed of solid precipitation. Geophys. Res. Lett. 41 (18), 6515–6522.Google Scholar
Gerashchenko, S., Sharp, N. S., Neuscamman, S. & Warhaft, Z. 2008 Lagrangian measurements of inertial particle accelerations in a turbulent boundary layer. J. Fluid Mech. 617, 225–281.Google Scholar
Gibert, M., Xu, H. & Bodenschatz, E. 2012 Where do small, weakly inertial particles go in a turbulent flow. J. Fluid Mech. 698, 160–167.Google Scholar
Good, G. H., Gerashchenko, S. & Warhaft, Z. 2012 Intermittency and inertial particle entrainment at a turbulent interface: the effect of the large-scale eddies. J. Fluid Mech. 694, 371–398.Google Scholar
Good, G. H., Ireland, P. J., Bewley, G. P. & Bodenschatz, E. 2014 Settling regimes of inertial particles in isotropic turbulence. J. Fluid Mech. 759, R3.Google Scholar
Gore, R. A. & Crowe, C. T. 1991 Modulation of turbulence by a dispersed phase. Trans. ASME J. Fluids Engng 113 (2), 304–307.Google Scholar
Goto, S. & Vassilicos, J. C. 2006 Self-similar clustering of inertial particles and zero-acceleration points in fully developed two-dimensional turbulence. Phys. Fluids 18, 115103.Google Scholar
Goto, S. & Vassilicos, J. C. 2008 Sweep-stick mechanism of heavy particle clustering in fluid turbulence. Phys. Rev. Lett. 100, 054503.Google Scholar
De Graff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Guala, M., Liberzon, A., Hoyer, K., Tsinober, A. & Kinzelbach, W. 2008 Experimental study on clustering of large particles in homogeneous turbulent flow. J. Turbul. 9, N34.Google Scholar
Gualtieri, P., Sardina, G., Picano, F. & Casciola, C. M. 2013 Clustering and turbulence modulation in particle-laden shear flows. J. Fluid Mech. 715, 134–162.Google Scholar
Gualtieri, P., Sardina, G., Picano, F. & Casciola, C. M. 2015 Exact regularized point particle method for multiphase flows in the two-way coupling regime. J. Flui Mech. 773, 520–561.Google Scholar
Gustavsson, K. & Mehlig, B. 2016 Statistical models for spatial patterns of heavy particles in turbulence. Adv. Phys. 65 (1), 1–57.Google Scholar
Gustavsson, K., Vajedi, S. & Mehlig, B. 2014 Clustering of particles falling in a turbulent flow. Phys. Rev. Lett. 112, 214501.Google Scholar
Hassan, Y. A., Blanchat, T. K. Jr. & Seeley, C. H. 1992 PIV flow visualisation using particle tracking techniques. Meas. Sci. Technol. 3 (7), 633.Google Scholar
Hearst, R. J., Buxton, O. R. H., Ganapathisubramani, B. & Lavoie, P. 2012 Experimental estimation of fluctuating velocity and scalar gradients in turbulence. Exp. Fluids 53 (4), 925–942.Google Scholar
Hetsroni, G. 1989 Particles–turbulence interaction. Intl J. Multiphase Flow 15 (5), 735–746.Google Scholar
Holtzer, G. L. & Collins, L. R. 2002 Relationship between the intrinsic radial distribution function for an isotropic field of particles and lower-dimensional measurements. J. Fluid Mech. 459, 93–102.Google Scholar
Horwitz, J. A. K. & Mani, A. 2016 Accurate calculation of Stokes drag for point particle tracking in two-way coupled flows. J. Comput. Phys. 318 (1), 85–109.Google Scholar
Huck, P. D., Bateson, C., Volk, R., Cartellier, A., Bourgoin, M. & Aliseda, A. 2018 The role of collective effects on settling velocity enhancement for inertial particles in turbulence. J. Fluid Mech. 846, 1059–1075.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Studying Turbulence Using Numerical Simulation Databases, 2. Proceedings of the 1988 Summer Program.Google Scholar
Hwang, W. & Eaton, J. K. 2006a Homogeneous and isotropic turbulence modulation by small heavy (st ∼ 50) particles. J. Fluid Mech. 564, 361–393.Google Scholar
Hwang, W. & Eaton, J. K. 2006b Turbulence attenuation by small particles in the absence of gravity. Intl J. Multiphase Flow 32 (12), 1386–1396.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016a The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 796, 617–658.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016b The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects. J. Fluid Mech. 796, 617–658.Google Scholar
Ireland, P. J. & Desjardins, O. 2017 Improving particle drag predictions in Euler–Lagrange simulations with two-way coupling. J. Comput. Phys. 338 (1), 405–430.Google Scholar
Ishima, T., Hishida, K. & Maeda, M. 1993 Effect of particle residence time on particle dispersion in a plane mixing layer. J. Fluids Engng 115 (4), 751–759.Google Scholar
Jenny, P., Roekaerts, D. & Beishuizen, N. 2012 Modeling of turbulent dilute spray combustion. Prog. Energy Combust. Sci. 38 (6), 846–887.Google Scholar
de Jong, J., Salazar, J. P. L. C., Woodward, S. H., Collins, L. R. & Meng, H. 2010 Measurement of inertial particle clustering and relative velocity statistics in isotropic turbulence using holographic imaging. Intl J. Multiphase Flow 36 (4), 324–332.Google Scholar
Kawanisi, K. & Shiozaki, R. 2008 Turbulent effects on the settling velocity of suspended sediment. J. Hydraul. Engng ASCE 134 (2), 261–266.Google Scholar
Khalitov, D. A. & Longmire, E. K. 2002 Simultaneous two-phase PIV by two-parameter phase discrimination. Exp. Fluids 32 (2), 252–268.Google Scholar
Khalitov, D. A. & Longmire, E. K. 2003 Effect of particle size on velocity correlations in turbulent channel flow. In ASME/JSME 2003 4th Joint Fluids Summer Engineering Conference, vol. 1: Fora, parts A, B, C, and D.Google Scholar
Kidanemariam, A. G., Chan-Braun, C., Doychev, T. & Uhlmann, M. 2013 Direct numerical simulation of horizontal open channel flow with finite-size, heavy particles at low solid volume fraction. New J. Phys. 15, 025031.Google Scholar
Kiger, K. T. & Pan, C. 2000 PIV technique for the simultaneous measurement of dilute two-phase flows. Trans. ASME J. Fluids Engng 122 (4), 811–818.Google Scholar
Kiger, K. T. & Pan, C. 2002 Suspension and turbulence modification effects of solid particulates on a horizontal turbulent channel flow. J. Turbul. 3, 19.Google Scholar
Kulick, J. D., Fessler, J. R. & Eaton, J. K. 1994 Particle response and turbulence modification in fully developed channel flow. J. Fluid Mech. 277, 109–134.Google Scholar
Lázaro, B. J. & Lasheras, J. C. 1989 Particle dispersion in a turbulent, plane, free shear layer. Phys. Fluids A 1, 1035–1044.Google Scholar
Longmire, E. K. & Eaton, J. K. 1992 Structure of a particle-laden round jet. J. Fluid Mech. 236, 217–257.Google Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.Google Scholar
Lucci, F., Frrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15, 2461.Google Scholar
Matsude, K., Onishi, R. & Takahashi, K. 2017 Influence of gravitational settling on turbulent droplet clustering and radar reflectivity factor. Flow Turbul. Combust. 98 (1), 327–340.Google Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
Maxey, M. R. & Corrsin, S. 1986 Free access gravitational settling of aerosol particles in randomly oriented cellular flow fields. J. Atmos. Sci. 43, 1112–1134.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.Google Scholar
Mei, R. 1994 Effect of turbulence on the particle settling velocity in the nonlinear drag range. Intl J. Multiphase Flow 20 (2), 273–284.Google Scholar
Mei, R., Adrian, R. J. & Hanratty, T. J. 1991 Particle dispersion in isotropic turbulence under Stokes drag and Basset force with gravitational settling. J. Fluid Mech. 225, 481–495.Google Scholar
Moisy, F. & Jiménez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.Google Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2010 Preferential concentration of heavy particles: a Voronoï analysis. Phys. Fluids 22 (10), 103304.Google Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2012 Analyzing preferential concentration and clustering of inertial particles in turbulence. Intl J. Multiphase Flow 40, 1–18.Google Scholar
Monchaux, R. & Dejoan, A. 2017 Settling velocity and preferential concentration of heavy particles under two-way coupling effects in homogeneous turbulence. Phys. Rev. Fluids 2, 104302.Google Scholar
Naso, A. & Prosperetti, A. 2010 The interaction between a solid particle and a turbulent flow. New J. Phys. 12 (3), 033040.Google Scholar
Nemes, A., Coletti, F., Fong, K. O. & Toloui, M. 2016 Experimental observation of three-dimensional particle clustering in turbulent channel flow. In International Conference on Multiphase Flows, Florence, Italy.Google Scholar
Nemes, A., Dasari, T., Hong, J., Guala, M. & Coletti, F. 2017 Snowflakes in the atmospheric surface layer: observation of particle turbulence dynamics. J. Fluid Mech. 814, 592–613.Google Scholar
Nemes, A., Jacono, D. L., Blackburn, H. M. & Sheridan, J. 2015 Mutual inductance of two helical vortices. J. Fluid Mech. 774, 298–310.Google Scholar
Nielsen, P. 1993 Turbulence effects on the settling of suspended particles. J. Sedim. Res. 63 (5), 835–838.Google Scholar
Obligado, M., Teitelbaum, T., Cartellier, A., Mininni, P. & Bourgoin, M. 2014 Preferential concentration of heavy particles in turbulence. J. Turbul. 15 (5), 293–310.Google Scholar
Ohmi, K. & Li, H. Y. 2000 Particle-tracking velocimetry with new algorithms. Meas. Sci. Technol. 11 (6), 603.Google Scholar
Paola, G. D., Kim, I. S. & Mastorakos, E. 2009 Second-order conditional moment closure simulations of autoignition of an n-heptane plume in a turbulent coflow of heated air. Flow Turbul. Combust. 82 (4), 455.Google Scholar
Paris, A. D.2001 Turbulence attenuation in a particle-laden channel flow. PhD thesis, Stanford University.Google Scholar
Perry, A. E. & Chong, M. S. 1994 Topology of flow patterns in vortex motions and turbulence. Appl. Sci. Res. 53 (3–4), 357–374.Google Scholar
Poelma, C. & Ooms, G. 2006 Particle–turbulence interaction in a homogeneous, isotropic turbulent suspension. ASME Appl. Mech. Rev. 59 (2), 78–90.Google Scholar
Poelma, C., Westerweel, J. & Ooms, G. 2007 Particle–fluid interactions in grid-generated turbulence. J. Fluid Mech. 589, 315–351.Google Scholar
Rabencov, B. & van Hout, R. 2015 Voronoï analysis of beads suspended in a turbulent square channel flow. Intl J. Multiphase Flow 68, 10–13.Google Scholar
Reade, W. C. & Collins, L. R. 2000 Effect of preferential concentration on turbulent collision rates. Phys. Fluids 12, 2530.Google Scholar
Reeks, M. W. 1977 On the dispersion of small particles suspended in an isotropic turbulent fluid. J. Fluid Mech. 83 (3), 529–546.Google Scholar
Rogers, C. B. & Eaton, J. K. 1991 The effect of small particles on fluid turbulence in a flat plate, turbulent boundary layer in air. Phys. Fluids A 3 (5), 928–937.Google Scholar
Rosa, B., Parishani, H., Ayala, O. & Wang, L.-P. 2016 Settling velocity of small inertial particles in homogeneous isotropic turbulence from high-resolution DNS. Intl J. Multiphase Flow 83, 217–231.Google Scholar
Rudoff, R. & Bachalo, W. 1988 Direct particle fluid simulation of Kolmogorov-length-scale size particles in decaying isotropic turbulence measurements of droplet drag coefficients in a polydispersed turbulent flow field. In 26th Aerospace Sciences Meeting. Reno, NV, USA.Google Scholar
Sabban, L. & van Hout, R. 2011 Measurements of pollen grain dispersal in still air and stationary, near homogeneous, isotropic turbulence. J. Aero. Sci. 42 (12), 867–882.Google Scholar
Sahu, S., Hardalupas, Y. & Taylor, A. M. K. P. 2014 Droplet turbulence interaction in a confined polydispersed spray: effect of droplet size and flow length scales on spatial droplet gas velocity correlations. J. Fluid Mech. 741, 98–138.Google Scholar
Sahu, S., Hardalupas, Y. & Taylor, A. M. K. P. 2016 Droplet turbulence interaction in a confined polydispersed spray: effect of turbulence on droplet dispersion. J. Fluid Mech. 794, 267–309.Google Scholar
Salazar, J. P. L. C. & Collins, L. R. 2012 Inertial particle acceleration statistics in turbulence: effects of filtering, biased sampling, and flow topology. Phys. Fluids 24, 083302.Google Scholar
Salazar, J. P. L. C., de Jong, J., Cao, L. & Woodward, S. H. 2008 Experimental and numerical investigation of inertial particle clustering in isotropic turbulence. J. Fluid Mech. 600, 245–256.Google Scholar
Saw, E.-W., Bewley, G. P., Bodenschatz, E., Ray, S. S. & Bec, J. 2014 Extreme fluctuations of the relative velocities between droplets in turbulent airflow. Phys. Fluids 26 (11), 111702.Google Scholar
Saw, E.-W., Debue, P., Kuzzay, D., Daviaud, F. & Dubrulle, B. 2018 On the universality of anomalous scaling exponents of structure functions in turbulent flows. J. Fluid Mech. 837, 657–669.Google Scholar
Saw, E. W., Shaw, R. A., Ayyalasomayajula, S., Chuang, P. Y. & Gylfason, A. 2008 Inertial clustering of particles in high-Reynolds-number turbulence. Phys. Rev. Lett. 100 (21), 214501.Google Scholar
Saw, E.-W., Shaw, R. A., Salazar, J. P. L. C. & Collins, L. R. 2012 Spatial clustering of polydisperse inertial particles in turbulence: II. Comparing simulation with experiment. New J. Phys. 14 (10), 105031.Google Scholar
Schanz, D., Gesemann, S. & Schröder, A. 2016 Shake-the-box: Lagrangian particle tracking at high particle image densities. Exp. Fluids 57 (5), 70.Google Scholar
Schneiders, L., Meinke, M. & Schroder, W. 2017 Direct particle-fluid simulation of Kolmogorov-length-scale size particles in decaying isotropic turbulence. J. Fluid Mech. 819, 188–227.Google Scholar
Shaw, R. A. 2003 Particle–turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35, 183–227.Google Scholar
Soldati, A. & Marchioli, C. 2009 Physics and modelling of turbulent particle deposition and entrainment: review of a systematic study. Intl J. Multiphase Flow 35 (9), 827–839.Google Scholar
Squires, K. D. & Eaton, J. K. 1990 Particle response and turbulence modification in isotropic turbulence. Phys. Fluid A 2, 1191–1203.Google Scholar
Squires, K. D. & Eaton, J. K. 1991a Measurements of particles dispersion obtained from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 226, 1–35.Google Scholar
Squires, K. D. & Eaton, J. K. 1991b Preferential concentration of particles by turbulence. Phys. Fluids A 3 (5), 1169–1178.Google Scholar
Sumbekova, S., Cartellier, A., Aliseda, A. & Bourgoin, M. 2017 Preferential concentration of inertial sub-Kolmogorov particles: the roles of mass loading of particles, Stokes numbers, and Reynolds numbers. Phys. Rev. Fluids 2, 024302.Google Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.Google Scholar
Sundaram, S. & Collins, L. R. 1999 A numerical study of the modulation of isotropic turbulence by suspended particles. J. Fluid Mech. 379, 105–143.Google Scholar
Tagawa, Y., Mercado, J. M., Prakash, V. N., Calzavarini, E., Sun, C. & Lohse, D. 2012 Three-dimensional Lagrangian Voronoï analysis for clustering of particles and bubbles in turbulence. J. Fluid Mech. 693, 201–215.Google Scholar
Tanaka, T. & Eaton, J. K. 2008 Classification of turbulence modification by dispersed spheres using a novel dimensionless number. Phys. Rev. Lett. 101, 114502.Google Scholar
Tanaka, T. & Eaton, J. K. 2010 Sub-Kolmogorov resolution partical image velocimetry measurements of particle-laden forced turbulence. J. Fluid Mech. 643, 177–206.Google Scholar
Tang, D. & Marangoni, A. G. 2006 3D fractal dimension of fat crystal networks. Chem. Phys. Lett. 433 (1–3), 248–252.Google Scholar
Tenneti, S. & Subramaniam, S. 2014 Particle-resolved direct numerical simulation for gas–solid flow model development. Annu. Rev. Fluid Mech. 46, 199–230.Google Scholar
Tooby, P. F., Wick, G. L. & Isaacs, J. D. 1977 The motion of a small sphere in a rotating velocity field: a possible mechanism for suspending particles in turbulence. J. Geophys. Res. 82 (15), 2096–2100.Google Scholar
Uhlmann, M. & Doychev, T. 2014 Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion. J. Fluid Mech. 752, 310–348.Google Scholar
Variano, E. A. & Cowen, E. A. 2008 A random-jet-stirred turbulence tank. J. Fluid Mech. 604, 1–32.Google Scholar
Volk, R., Calzavarini, E., Verhille, G., Lohse, D., Mordant, N., Pinton, J.-F. & Toschi, F. 2008 Acceleration of heavy and light particles in turbulence: comparison between experiments and direct numerical simulations. Physica D 237 (14–17), 2084–2089.Google Scholar
Wang, L.-P., Ayala, O. & Grabowski, W. W. 2007 Effects of aerodynamic interactions on the motion of heavy particles in a bidisperse suspension. J. Turbul. 8, N25.Google Scholar
Wang, L.-P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Wang, L.-P. & Stock, D. E. 1993 Dispersion of heavy particles by turbulent motion. J. Atmos. Sci. 50, 1897–1913.Google Scholar
Wang, L.-P., Wexler, A. S. & Zhou, Y. 2000 Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech. 415, 117–153.Google Scholar
Warnica, W. D., Renksizbulut, M. & Strong, A. B. 1995 Drag coefficients of spherical liquid droplets. Part 2. Turbulent gaseous fields. Exp. Fluids 18 (4), 265–276.Google Scholar
Wells, M. R. & Stock, D. E. 1983 The effects of crossing trajectories on the dispersion of particles in a turbulent flow. J. Fluid Mech. 136, 31–62.Google Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39, 1096–1100.Google Scholar
Wilkinson, M. & Mehlig, B. 2005 Caustics in turbulent aerosols. Europhys. Lett. 71 (2), 186.Google Scholar
Woittiez, E. J. P., Jonker, H. J. J. & Portela, L. 2009 On the combined effects of turbulence and gravity on droplet collisions in clouds: a numerical study. J. Atmos. Sci. 66 (7), 1926–1943.Google Scholar
Wood, A. M., Hwang, W. & Eaton, J. K. 2005 Preferential concentration of particles in homogeneous and isotropic turbulence. Intl J. Multiphase Flow 31 (10–11), 1220–1230.Google Scholar
Worth, N. A., Nickels, T. B. & Swaminathan, N. 2010 A tomographic PIV resolution study based on homogeneous isotropic turbulence DNS data. Exp. Fluids 49 (3), 637–656.Google Scholar
Wu, J.-S. & Faeth, G. M. 1994 Sphere wakes at moderate Reynolds numbers in a turbulent environment. AIAA J. 32 (3), 535–54166.Google Scholar
Yang, C. Y. & Lei, U. 1998 The role of the turbulent scales in the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 371, 179–205.Google Scholar
Yang, T. S. & Shy, S. S. 2003 The settling velocity of heavy particles in an aqueous near-isotropic turbulence. Phys. Fluids 15 (4), 868–880.Google Scholar
Yang, T. S. & Shy, S. S. 2005 Two-way interaction between solid particles and homogeneous air turbulence: particle settling rate and turbulence modification measurements. J. Fluid Mech. 526, 171–216.Google Scholar
Yoshimoto, H. & Goto, S. 2007 Self-similar clustering of inertial particles in homogeneous turbulence. J. Fluid Mech. 577, 275–286.Google Scholar
Yudine, M. I. 1959 Physical considerations on heavy-particle diffusion. Adv. Geophys. 6, 185–191.Google Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2009 Statistical models for predicting pair dispersion and particle clustering in isotropic turbulence and their applications. New J. Phys. 11, 103018.Google Scholar
Zamansky, R., Coletti, F., Massot, M. & Mani, A. 2016 Turbulent thermal convection driven by heated inertial particles. J. Fluid Mech. 809, 390–437.Google Scholar
Zhao, L. H., Marchioli, C. & Andersson, H. I. 2012 Stokes number effects on particle slip velocity in wall-bounded turbulence and implications for dispersion models. Phys. Fluids 24, 021705.Google Scholar