Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T01:02:12.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study of flow around polygonal cylinders

Published online by Cambridge University Press:  22 December 2016

S. J. Xu ,
W. G. Zhang ,
L. Gan ,
M. G. Li  and
Y. Zhou
S. J. Xu*
Affiliation:
School of Aerospace Engineering, Tsinghua University, 100084, China
W. G. Zhang
Affiliation:
School of Aeronautics, Northwestern University, Xi’an 710072, China
L. Gan*
Affiliation:
School of Engineering and Computing Sciences, Durham University, DH1 3LE, UK
M. G. Li
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Y. Zhou
Affiliation:
Institute of Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, 518055, China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

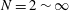The wake of polygonal cylinders with side number $N=2\sim \infty$ is systematically studied based on fluid force, hot-wire, particle image velocimetry and flow visualisation measurements. Each cylinder is examined for two orientations, with a flat surface or a corner leading and facing normally to the free stream. The Reynolds number 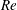$Re$ is 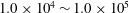$1.0\times 10^{4}\sim 1.0\times 10^{5}$, based on the longitudinally projected cylinder width. The time-averaged drag coefficient 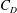$C_{D}$ and fluctuating lift coefficient on these cylinders are documented, along with the characteristic properties including the Strouhal number 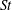$St$, flow separation point and angle 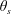$\unicode[STIX]{x1D703}_{s}$, wake width and critical Reynolds number 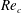$Re_{c}$ at which the transition from laminar to turbulent flow occurs. It is found that once 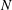$N$ exceeds 12, 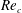$Re_{c}$ depends on the difference between the inner diameter (tangent to the faces) and the outer diameter (connecting corners) of a polygon, the relationship being approximately given by the dependence of 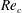$Re_{c}$ on the height of the roughness elements for a circular cylinder. It is further found that 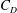$C_{D}$ versus 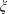$\unicode[STIX]{x1D709}$ or 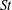$St$ versus 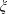$\unicode[STIX]{x1D709}$ for all the tested cases collapse onto a single curve, where the angle 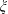$\unicode[STIX]{x1D709}$ is the corrected 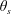$\unicode[STIX]{x1D703}_{s}$ associated with the laterally widest point of the polygon and the separation point. Finally, the empirical correlation between $C_{D}$ and 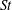$St$ is discussed.

JFM classification

Turbulent Flows: Turbulent transition Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 251 - 278
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlborn, B., Seto, M. L. & Noack, B. R. 2002 On drag, Strouhal number and vortex-street structure. Fluid Dyn. Res. 30, 379–399.CrossRefGoogle Scholar
Alam, M. M. & Zhou, Y. 2007 Turbulent wake of an inclined cylinder with water running. J. Fluid Mech. 589, 261–303.CrossRefGoogle Scholar
Alam, M. M. & Zhou, Y. 2008 Alternative drag coefficient in the wake of an isolated bluff body. Phys. Rev. E 78, 036320.Google ScholarPubMed
Antonia, R. A. & Rajagopalan, S. 1990 Determination of drag of a circular cylinder. AIAA J. 28 (10), 1833–1834.Google Scholar
Bearman, P. 1967 On vortex street wakes. J. Fluid Mech. 28, 625–641.CrossRefGoogle Scholar
Bearman, P. W. 1969 On vortex shedding from a circular cylinder in the critical Reynolds number regime. J. Fluid Mech. 37, 577–585.Google Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.CrossRefGoogle Scholar
Blevins, B. D. 1990 Flow-induced Vibration, 2nd edn., p. 50. Van Nostrand Reinhold.Google Scholar
Bosch, H. R. & Guterres, R. M. 2001 Wind tunnel experimental investigation on tapered cylinders for highway support structures. J. Wind Engng Ind. Aerodyn. 89, 1311–1323.CrossRefGoogle Scholar
Cowdrey, C. F.1962 A note on the use of end plates to prevent three dimensional flow at the ends of bluff bodies. NPL Aero Rep. 1025.Google Scholar
Deniz, S. & Staubli, T. H. 1997 Oscilating rectangular and octagonal profiles: interaction of leading- and trailing-edge vortex formation. J. Fluids Struct. 11, 3–31.Google Scholar
Gerich, D. & Echelmann, H. 1982 Influence of end plates and free ends on the shedding frequency of circular cylinders. J. Fluid Mech. 122, 109–121.Google Scholar
Gerrard, J. H. 1966 The mechanics of the formation region of vortices behind bluff bodies. J. Fluid Mech. 25 (02), 401–413.Google Scholar
Güven, O., Farell, C. & Patel, V. C. 1980 Surface-roughness effects on the mean flow past circular cylinders. J. Fluid Mech. 98 (4), 673–701.CrossRefGoogle Scholar
Hoerner, S. F.1965 Fluid-Dynamic Drag, Practical Information on Aerodynamic Drag and Hydrodynamic Resistance, pp. 0–2, 2–8. Published by the Author.Google Scholar
Khaledi, H. A. & Andersson, H. I. 2011 On vortex shedding from a hexagonal cylinder. Phys. Lett. A 375, 4007–4021.Google Scholar
Matsumoto, M. 1999 Vortex shedding of bluff bodies: a review. J. Fluids Struct. 13, 791–811.CrossRefGoogle Scholar
Mills, R., Sheridan, J. & Hourigan, K. 2003 Particle image velocimetry and visualization of natural and forced flow around rectangular cylinders. J. Fluid Mech. 478, 299–323.Google Scholar
Norberg, C. 1994 An experimental investigation of the flow around a circular cylinder: influence of aspect ratio. J. Fluid Mech. 258, 287–316.Google Scholar
Norberg, C. 2003 Fluctuating lift on a circular cylinder: review and new measurements. J. Fluids Struct. 17, 57–96.Google Scholar
Okajima, A. 1982 Strouhal numbers of rectangular cylinders. J. Fluid Mech. 123, 379–398.Google Scholar
Ponta, F. L. 2006 Effect of shear-layer thickness on the Strouhal Reynolds number relationship for bluff-body wakes. J. Fluids Struct. 22, 1133–1138.Google Scholar
Roshko, A. 1955 On the wake and drag of bluff bodies. J. Aero. Sci. 22, 124–132.Google Scholar
Saffman, P. G. 1995 Vortex Dynamics. Cambridge University Press.Google Scholar
Schewe, G. & Larsen, A. 1988 Reynolds number effects in the flow around a bluff bridge deck cross section. J. Wind Engng Ind. Aerodyn. 74, 829–838.Google Scholar
Skews, B. W. 1991 Autorotation of many-sided bodies in an airstream. Nature 352, 512–513.Google Scholar
Skews, B. W. 1998 Autorotation of polygonal prisms with an upstream vane. J. Wind Engng Ind. Aerodyn. 73, 145–158.CrossRefGoogle Scholar
Srigrarom, S. & Koh, A. K. G. 2008 Flow field of self-excited rotationally oscillating equilateral triangular cylinder. J. Fluids Struct. 24, 750–755.CrossRefGoogle Scholar
Szepessy, S. & Bearman, P. W. 1992 Aspect ratio and end plate effects on vortex shedding from a circular cylinder. J. Fluid Mech. 234, 191–217.CrossRefGoogle Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wake. J. Fluids Struct. 15, 607–616.CrossRefGoogle Scholar
Tian, X. & Li, S. 2007 Scientific measurements of disturbance on the prototype stands in a low speed wind tunnel. Exp. Res. Aerodyn. 25 (3), 1–6 (in Chinese).Google Scholar
Tian, Z. W. & Wu, Z. N. 2009 A study of two-dimensional flow past regular polygons via conformal mapping. J. Fluid Mech. 628, 121–154.Google Scholar
Tropea, C., Yarin, A. & Foss, J. F.(Eds) 2007 Springer Handbook of Experimental Fluid Mechanics, pp. 1125–1145. Springer.Google Scholar
Vickery, B. J. 1966 Fluctuating lift and drag on a long cylinder of square cross-section in a smooth and in a turbulent stream. J. Fluid Mech. 25, 481–494.Google Scholar
West, G. S. & Apelt, C. J. 1982 The effects of tunnel blockage and aspect ratio on the mean flow past a circular cylinder with Reynolds numbers between 104 and 105. J. Fluid Mech. 114, 361–377.Google Scholar
White, F. W. 2001 Physics – Fluid Mechanics, 4th edn., pp. 277–311, 427–476. McGraw-Hill.Google Scholar
Wieselsberger, C. 1921 Recent statements on the laws of liquid and air resistency. Phys. Z. 22, 321–328.Google Scholar
Williamson, C. H. K. 1988 Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 31 (10), 2742–2744.CrossRefGoogle Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
Williamson, C. H. K. & Brown, G. L. 1998 A series in 1/√Re to represent the Strouhal–Reynolds number relationship for the cylinder wake. J. Fluid Struct. 12 (8), 1073–1085.CrossRefGoogle Scholar
Yamagishi, Y., Kimura, S. & Makoto, O. 2010 Flow characteristics around a square cylinder with changing chamfer dimensions. J. Vis. 13 (1), 61–68.Google Scholar
Yeung, W. W. H. 2009 On pressure invariance, wake width and drag prediction of a bluff body in confined flow. J. Fluid Mech. 622, 321–344.Google Scholar
Yeung, W. W. H. 2010 On the relationships among Strouhal number, pressure drag, and separation pressure for blocked bluff-body flow. Trans. ASME J. Fluids Engng 132 (2), 021201.Google Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders, vol. 1. Oxford University Press.Google Scholar