Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-21T08:14:36.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of flow-induced vibration of a sinusoidally rotating circular cylinder

Published online by Cambridge University Press:  05 June 2018

K. W. L. Wong ,
J. Zhao Open the ORCID record for J. Zhao [Opens in a new window] ,
D. Lo Jacono Open the ORCID record for D. Lo Jacono [Opens in a new window] ,
M. C. Thompson  and
J. Sheridan
K. W. L. Wong
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
J. Zhao*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
D. Lo Jacono
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse, France
M. C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
J. Sheridan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The present experimental investigation characterises the dynamic response and wake structure of a sinusoidally rotating circular cylinder with a low mass ratio (defined as the ratio of the total oscillating mass to the displaced fluid mass) undergoing cross-stream flow-induced vibration (FIV). The study covers a wide parameter space spanning the forcing rotary oscillation frequency ratio 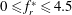$0\leqslant f_{r}^{\ast }\leqslant 4.5$ and the forcing rotation speed ratio 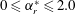$0\leqslant \unicode[STIX]{x1D6FC}_{r}^{\ast }\leqslant 2.0$, at reduced velocities associated with the vortex-induced vibration (VIV) upper and lower amplitude response branches. Here, 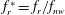$f_{r}^{\ast }=f_{r}/f_{nw}$ and 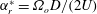$\unicode[STIX]{x1D6FC}_{r}^{\ast }=\unicode[STIX]{x1D6FA}_{o}D/(2U)$, where 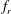$f_{r}$ is the forcing rotary oscillation frequency, 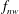$f_{nw}$ is the natural frequency of the system in quiescent fluid (water), 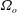$\unicode[STIX]{x1D6FA}_{o}$ is the peak angular rotation speed, 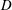$D$ is the cylinder diameter and 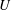$U$ is the free-stream velocity; the reduced velocity is defined by 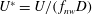$U^{\ast }=U/(\,f_{nw}D)$. The fluid–structure system was modelled using a low-friction air-bearing system in conjunction with a free-surface recirculating water channel, with axial rotary motion provided by a microstepping motor. The cylinder was allowed to vibrate with only one degree of freedom transverse to the oncoming free-stream flow. It was found that in specific ranges of 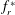$f_{r}^{\ast }$, the body vibration frequency may deviate from that seen in the non-rotating case and lock onto the forcing rotary oscillation frequency or its one-third subharmonic. The former is referred to as the ‘rotary lock-on’ (RLO) region and the latter as the ‘tertiary lock-on’ (TLO) region. Significant increases in the vibration amplitude and suppression of VIV could both be observed in different parts of the RLO and TLO regions. The peak amplitude response in the case of 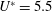$U^{\ast }=5.5$ (upper branch) was observed to be 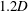$1.2D$, an increase of approximately 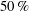$50\,\%$ over the non-rotating case, while in the case of 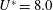$U^{\ast }=8.0$ (lower branch), the peak amplitude response was 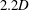$2.2D$, a remarkable increase of 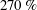$270\,\%$ over the non-rotating case. Notably, the results showed that the amplitude responses at moderate Reynolds numbers (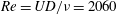$Re=UD/\unicode[STIX]{x1D708}=2060$ and 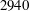$2940$, where $\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid) in the present study showed significant differences from those of a previous low-Reynolds-number (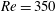$Re=350$) numerical study at similar reduced velocities by Du & Sun (Phys. Fluids, vol. 14 (8), 2015, pp. 2767–2777). Remarkably, in an additional study examining the cylinder vibration as a function of 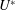$U^{\ast }$ while the fixed forcing rotary oscillation parameters were kept constant at $(f_{r}^{\ast },\unicode[STIX]{x1D6FC}_{r}^{\ast })=(1.0,1.0)$, the cylinder experienced substantially larger oscillations than in the non-rotating case, and a rotation-induced galloping response was observed for 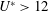$U^{\ast }>12$, where the amplitude increased monotonically to reach approximately 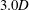$3.0D$ at the highest reduced velocity ($U^{\ast }=20$) tested. Furthermore, new wake modes were identified in the RLO and TLO regions using particle image velocimetry measurements at selected points in the 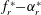$f_{r}^{\ast }-\unicode[STIX]{x1D6FC}_{r}^{\ast }$ parameter space.

JFM classification

Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 430 - 466
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baek, S.-J. & Sung, H. J. 1998 Numerical simulation of the flow behind a rotary oscillating circular cylinder. Phys. Fluids 10 (4), 869–876.Google Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16 (1), 195–222.Google Scholar
Bishop, R. E. D. & Hassan, A. Y. 1964 The lift and drag forces on a circular cylinder in a flowing fluid. Proc. R. Soc. Lond. A 277 (1368), 32–50.Google Scholar
Blevins, R. D. 1990 Flow-Induced Vibration, 2nd edn. Krieger Publishing Company.Google Scholar
Bokaian, A. & Geoola, F. 1984 Wake-induced galloping of two interfering circular cylinders. J. Fluid Mech. 146, 383–415.Google Scholar
Brooks, P. N. H.1960 Experimental investigation of the aeroelastic instability of bluff two-dimensional cylinders. Masters, University of British Columbia.Google Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2001 Forces and wake modes of an oscillating cylinder. J. Fluids Struct. 15 (1), 523–532.CrossRefGoogle Scholar
Cheng, M. 2001 Numerical investigation of a rotationally oscillating cylinder in mean flow. J. Fluids Struct. 15, 981–1007.Google Scholar
Cheng, M., Liu, G. & Lam, K. 2001 Numerical simulation of flow past a rotationally oscillating cylinder. Comput. Fluids 30 (3), 365–392.CrossRefGoogle Scholar
Choi, S., Choi, H. & Kang, S. 2002 Characteristics of flow over a rotationally oscillating cylinder at low Reynolds number. Phys. Fluids 14 (8), 2767–2777.Google Scholar
Chou, M.-H. 1997 Synchronization of vortex shedding from a cylinder under rotary oscillation. Comput. Fluids 26 (8), 755–774.CrossRefGoogle Scholar
Du, L. & Sun, X. 2015 Suppression of vortex-induced vibration using the rotary oscillation of a cylinder. Phys. Fluids 27 (2), 023603.Google Scholar
Feng, C. C.1968 The measurement of vortex induced effects in flow past stationary and oscillating circular and D-section cylinders. Masters, The University of British Columbia.Google Scholar
Fouras, A., Lo Jacono, D. & Hourigan, K. 2008 Target-free stereo PIV: a novel technique with inherent error estimation and improved accuracy. Exp. Fluids 44 (2), 317–329.Google Scholar
Gabbai, R. D. & Benaroya, H. 2005 An overview of modeling and experiments of vortex-induced vibration of circular cylinders. J. Sound Vib. 282 (3), 575–616.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2006 Defining the ‘modified Griffin plot’ in vortex-induced vibration: revealing the effect of Reynolds number using controlled damping. J. Fluid Mech. 561, 147–180.Google Scholar
Griffin, O. M., Skop, R. A. & Koopmann, G. H. 1973 The vortex-excited resonant vibrations of circular cylinders. J. Sound Vib. 31 (2), 235–249.Google Scholar
Khalak, A. & Williamson, C. H. K. 1997 Fluid forces and dynamics of a hydroelastic structure with very low mass and damping. J. Fluids Struct. 11, 973–982.Google Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13, 813–851.Google Scholar
Morse, T. L. & Williamson, C. H. K. 2009 Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 634, 5–39.Google Scholar
Naudascher, E. & Rockwell, D. 2005 Flow-Induced Vibrations: An Engineering Guide. Dover Publications Inc.Google Scholar
Nemes, A., Zhao, J., Lo Jacono, D. & Sheridan, J. 2012 The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack. J. Fluid Mech. 710, 102–130.Google Scholar
Okajima, A., Takata, H. & Asanuma, T. 1975 Viscous flow around a rotationally oscillating circular cylinder. ISAS Report 12, 311–338.Google Scholar
Païdoussis, M., Price, S. & De Langre, E. 2010 Fluid–Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Sareen, A., Zhao, J., Lo Jacono, D., Sheridan, J., Hourigan, K. & Thompson, M. C. 2018 Vortex-induced vibration of a rotating sphere. J. Fluid Mech. 837, 258–292.Google Scholar
Sarpkaya, T. 1995 Hydrodynamic damping, flow-induced oscillations, and biharmonic response. J. Offshore Mech. Arctic Engng 117, 232–238.CrossRefGoogle Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.Google Scholar
Taneda, S. 1978 Visual observations of the flow past a circular cylinder performing a rotatory oscillation. J. Phys. Soc. Japan 45 (3), 1038–1043.Google Scholar
Thiria, B., Goujon-Durand, S. & Wesfreid, J. 2006 The wake of a cylinder performing rotary oscillations. J. Fluid Mech. 560, 123–147.Google Scholar
Tokumaru, P. T. & Dimotakis, P. E. 1991 Rotary oscillation control of a cylinder wake. J. Fluid Mech. 224, 77–90.Google Scholar
Williamson, C. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36 (1), 413–455.Google Scholar
Wong, K. W. L., Zhao, J., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2017 Experimental investigation of flow-induced vibration of a rotating circular cylinder. J. Fluid Mech. 829, 486–511.CrossRefGoogle Scholar
Xiao, Q. & Zhu, Q. 2014 A review on flow energy harvesters based on flapping foils. J. Fluids Struct. 46, 174–191.CrossRefGoogle Scholar
Young, J., Lai, J. C. & Platzer, M. F. 2014 A review of progress and challenges in flapping foil power generation. Prog. Aerosp. Sci. 67, 2–28.Google Scholar
Zhao, J., Leontini, J. S., Lo Jacono, D. & Sheridan, J. 2014a Chaotic vortex induced vibrations. Phys. Fluids 26 (12), 121702.Google Scholar
Zhao, J., Leontini, J. S., Lo Jacono, D. & Sheridan, J. 2014b Fluid–structure interaction of a square cylinder at different angles of attack. J. Fluid Mech. 747, 688–721.Google Scholar
Zhao, J., Lo Jacono, D., Sheridan, J., Hourigan, K. & Thompson, M. C. 2018 Experimental investigation of in-line flow-induced vibration of a rotating cylinder. J. Fluid Mech. 847, 664–699.Google Scholar

Wong et al. supplementary movie 1

Phase-averaged vorticity contours showing the 2Po pattern at (fr∗, αr∗) = (1.0, 1.0) in the RLO region of the U∗ = 5.5 case.

Download Wong et al. supplementary movie 1(Video)
Video 3.4 MB

Wong et al. supplementary movie 2

Phase-averaged vorticity contours showing the 2S pattern at (fr∗, αr∗) = (1.0, 2.0) in the U∗ = 5.5 case.

Download Wong et al. supplementary movie 2(Video)
Video 3.7 MB

Wong et al. supplementary movie 3

Phase-averaged vorticity contours showing the 2S pattern at (fr∗, αr∗) = (3.0, 2.0) in the U∗ = 5.5 case.

Download Wong et al. supplementary movie 3(Video)
Video 3.1 MB

Wong et al. supplementary movie 4

Phase-averaged vorticity contours showing the 4S pattern at (fr∗, αr∗) = (3.0, 1.0) in the TLO region of the U∗ = 5.5 case.

Download Wong et al. supplementary movie 4(Video)
Video 3.4 MB

Wong et al. supplementary movie 5

Phase-averaged vorticity contours showing the 4S pattern at (fr∗, αr∗) = (1.0, 1.5) in the RLO region of the U∗ = 8.0 case.

Download Wong et al. supplementary movie 5(Video)
Video 2.4 MB

Wong et al. supplementary movie 6

Phase-averaged vorticity contours showing the 2(Po+S) pattern at (fr∗, αr∗) = (3.0, 1.0) in the TLO region of the U∗ = 8.0 case.

Download Wong et al. supplementary movie 6(Video)
Video 3.1 MB