Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T04:54:09.320Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental evidence of new three-dimensional modes in the wake of a rotating cylinder

Published online by Cambridge University Press:  14 October 2013

A. Radi ,
M. C. Thompson ,
A. Rao ,
K. Hourigan  and
J. Sheridan
A. Radi
Affiliation:
Fluids Laboratory for Industrial and Aeronautical Research, FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, VIC, 3800, Australia
M. C. Thompson*
Affiliation:
Fluids Laboratory for Industrial and Aeronautical Research, FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, VIC, 3800, Australia
A. Rao
Affiliation:
Fluids Laboratory for Industrial and Aeronautical Research, FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, VIC, 3800, Australia
K. Hourigan
Affiliation:
Fluids Laboratory for Industrial and Aeronautical Research, FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, VIC, 3800, Australia Division of Biological Engineering, Monash University, VIC, 3800, Australia
J. Sheridan
Affiliation:
Fluids Laboratory for Industrial and Aeronautical Research, FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, VIC, 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A recent numerical study by Rao et al. (J. Fluid Mech., vol. 717, 2013, pp. 1–29) predicted the existence of several previously unobserved linearly unstable three-dimensional modes in the wake of a spinning cylinder in cross-flow. While linear stability analysis suggests that some of these modes exist for relatively limited ranges of Reynolds numbers and rotation rates, this may not be true for fully developed nonlinear wakes. In the current paper, we present the results of water channel experiments on a rotating cylinder in cross-flow, for Reynolds numbers 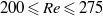$200\leqslant \mathit{Re}\leqslant 275$ and non-dimensional rotation rates 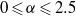$0\leqslant \alpha \leqslant 2. 5$. Using particle image velocimetry and digitally post-processed hydrogen bubble flow visualizations, we confirm the existence of the predicted modes for the first time experimentally. For instance, for 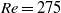$\mathit{Re}= 275$ and a rotation rate of 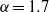$\alpha = 1. 7$, we observe a subharmonic mode, mode C, with a spanwise wavelength of 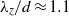${\lambda }_{z} / d\approx 1. 1$. On increasing the rotation rate, two modes with a wavelength of 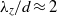${\lambda }_{z} / d\approx 2$ become unstable in rapid succession, termed modes D and E. Mode D grows on a shedding wake, whereas mode E consists of streamwise vortices on an otherwise steady wake. For 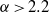$\alpha \gt 2. 2$, a short-wavelength mode F appears localized close to the cylinder surface with 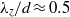${\lambda }_{z} / d\approx 0. 5$, which is presumably a manifestation of centrifugal instability. Unlike the other modes, mode F is a travelling wave with a spanwise frequency of 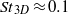${\mathit{St}}_{3D} \approx 0. 1$. In addition to these new modes, observations on the one-sided shedding process, known as the ‘second shedding’, are reported for 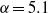$\alpha = 5. 1$. Despite suggestions from the literature, this process seems to be intrinsically three-dimensional. In summary, our experiments confirm the linear predictions by Rao et al., with very good agreement of wavelengths, symmetries and the phase velocity for the travelling mode. Apart from this, these experiments examine the nonlinear saturated state of these modes and explore how the existence of multiple unstable modes can affect the selected final state. Finally, our results establish that several distinct three-dimensional instabilities exist in a relatively confined area on the 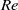$\mathit{Re}$–$\alpha $ parameter map, which could account for their non-detection previously.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Vortex streets Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 734 , 10 November 2013 , pp. 567 - 594
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Barkley, D., Tuckerman, L. S. & Golubitsky, M. 2000 Bifurcation theory for three-dimensional flow in the wake of a circular cylinder. Phys. Rev. E 61 (5), 5247–5252.CrossRefGoogle ScholarPubMed
Bénard, H. 1908 Formation de centres de giration à l’arriere d’un obstacle en mouvement. C. R. Acad. Sci. Paris 147, 839–842.Google Scholar
Blackburn, H. M. & Lopez, J. M. 2003 On three-dimensional quasi-periodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15, L57–L60.CrossRefGoogle Scholar
Cimbala, J., Nagib, H. & Roshko, A. 1988 Large structure in the far wakes of two-dimensional bluff bodies. J. Fluid Mech. 190, 265–298.CrossRefGoogle Scholar
Délery, J. M. 2001 Robert Legendre and Henri Werlé: toward the elucidation of three-dimensional separation. Annu. Rev. Fluid Mech. 33 (1), 129–154.CrossRefGoogle Scholar
Dusek, J., Le Gal, P. & Fraunie, D. P. 1994 A numerical and theoretical study of the first Hopf bifurcation in a cylinder wake. J. Fluid Mech. 264, 59–80.CrossRefGoogle Scholar
El Akoury, R., Braza, M., Perrin, R., Harran, G. & Hoarau, Y. 2008 The three-dimensional transition in the flow around a rotating cylinder. J. Fluid Mech. 607, 1–11.CrossRefGoogle Scholar
Fouras, A., Lo Jacono, D. & Hourigan, K. 2008 Target-free stereo PIV: a novel technique with inherent error estimation and improved accuracy. Exp. Fluids 44 (2), 317–329.CrossRefGoogle Scholar
Henderson, R. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.CrossRefGoogle Scholar
Jackson, C. P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182, 23–45.CrossRefGoogle Scholar
Kármán, Th. Von 1911 Über den Mechanismus des Widerstandes, den ein bewegter Körper in einer Flüsseigkeit erfährt. Gött. Nachr 5, 509–517.Google Scholar
Kerr, O. S. & Dold, J. W. 1994 Periodic steady vortices in a stagnation-point flow. J. Fluid Mech. 276, 307–325.CrossRefGoogle Scholar
Kumar, B. & Mittal, S. 2006 Effect of blockage on critical parameters for flow past a circular cylinder. Intl J. Numer. Meth. Fluids 50 (8), 987–1001.CrossRefGoogle Scholar
Kumar, S, Cantu, C. & Gonzalez, B. 2011 Flow past a rotating cylinder at low and high rotation rates. J. Fluids Engng 133 (4), 041201.CrossRefGoogle Scholar
Le Gal, P., Nadim, A. & Thompson, M. C. 2001 Hysteresis in the forced Stuart–Landau equation: application to vortex shedding from an oscillating cylinder. J. Fluids Struct. 15, 445–457.CrossRefGoogle Scholar
Leblanc, S. & Godeferd, F. S. 1999 An illustration of the link between ribs and hyperbolic instability. Phys. Fluids 11 (2), 497–499.CrossRefGoogle Scholar
Leweke, T. & Williamson, C. H. K. 1998a Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85–119.CrossRefGoogle Scholar
Leweke, T. & Williamson, C. H. K. 1998b Three-dimensional instabilities in wake transition. Eur. J. Mech. (B/Fluids) 17, 571–586.CrossRefGoogle Scholar
Luo, S. C., Chew, Y. T. & Duong, T. T. L. 2009 PIV investigation of flow past a rotating circular cylinder. In Fourth International Conference on Experimental Mechanics, Proc. SPIE, vol. 7522, International Society for Optics and Photonics, article 752219.Google Scholar
Miller, G. D. & Williamson, C. H. K. 1994 Control of three-dimensional phase dynamics in a cylinder wake. Exp. Fluids 18 (1), 26–35.CrossRefGoogle Scholar
Mittal, S. 2001 Flow past rotating cylinders: effect of eccentricity. Trans. ASME: J. Appl. Mech. 68 (4), 543–552.CrossRefGoogle Scholar
Mittal, S. 2004 Three-dimensional instabilities in flow past a rotating cylinder. Trans. ASME: J. Appl. Mech. 71 (1), 89–96.CrossRefGoogle Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.CrossRefGoogle Scholar
Norberg, C. 1987 Effect of Reynolds number and a low-intensity free stream turbulence on the flow around a circular cylinder. PhD thesis, Chalmers University of Technology, Gothenburg, Sweden.Google Scholar
Pralits, J., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
Pralits, J. O., Giannetti, F. & Brandt, L. 2013 Three-dimensional instability of the flow around a rotating circular cylinder. J. Fluid Mech. 730, 5–18.CrossRefGoogle Scholar
Prasad, A. & Williamson, C. H. K. 1997 Three-dimensional effects in turbulent bluff-body wakes. J. Fluid Mech. 343, 235–265.CrossRefGoogle Scholar
Rao, A., Leontini, J., Thompson, M. C. & Hourigan, K. 2013a Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.CrossRefGoogle Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2013b Three-dimensionality in the wake of a rapidly rotating cylinder in uniform flow. J. Fluid Mech. 730, 379–391.CrossRefGoogle Scholar
Ryan, K., Thompson, M. C. & Hourigan, K. 2005 Three-dimensional transition in the wake of elongated bluff bodies. J. Fluid Mech. 538, 1–29.CrossRefGoogle Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2003a A coupled Landau model describing the Strouhal–Reynolds number profile of the three-dimensional wake of a circular cylinder. Phys. Fluids 15 (9), L68–L71.CrossRefGoogle Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2003b From spheres to circular cylinders: the stability and flow structures of bluff ring wakes. J. Fluid Mech. 492, 147–180.CrossRefGoogle Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2005a The subharmonic mechanism of the mode C instability. Phys. Fluids 17 (11), 111702.CrossRefGoogle Scholar
Sheard, G. J., Thompson, M. C., Hourigan, K. & Leweke, T. 2005b The evolution of a subharmonic mode in a vortex street. J. Fluid Mech. 534, 23–38.CrossRefGoogle Scholar
Smits, A. J. & Lim, T. T. 2000 Flow Visualization: Techniques and Examples, 1st edn. Imperial College Press.CrossRefGoogle Scholar
Stojković, D., Schön, P., Breuer, M. & Durst, F. 2003 On the new vortex shedding mode past a rotating circular cylinder. Phys. Fluids 15, 1257–1260.CrossRefGoogle Scholar
Thompson, M., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12 (2), 190–196.CrossRefGoogle Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.CrossRefGoogle Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31 (11), 3165–3168.CrossRefGoogle Scholar
Williamson, C. H. K. 1992 The natural and forced formation of spot-like ‘vortex dislocations’ in the transition of a wake. J. Fluid Mech. 243, 393–441.CrossRefGoogle Scholar
Williamson, C. H. K. 1996a Mode A secondary instability in wake transition. Phys. Fluids 8 (6), 1680–1682.CrossRefGoogle Scholar
Williamson, C. H. K. 1996b Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Williamson, C. H. K. 1996c Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar
Wu, J., Sheridan, J., Welsh, M. C. & Hourigan, K. 1996 Three-dimensional vortex structures in a cylinder wake. J. Fluid Mech. 312, 201–222.CrossRefGoogle Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2010 Vortex dynamics in a wire-disturbed cylinder wake. Phys. Fluids 22 (9), 094101.CrossRefGoogle Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013 Mode C flow transition behind a circular cylinder with a near-wake wire disturbance. J. Fluid Mech. 727, 30–55.CrossRefGoogle Scholar
Zhang, H.-Q., Fey, U., Noack, B., König, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7 (4), 779–794.CrossRefGoogle Scholar

Radi et al. supplememntary movie

This video shows all investigated three-dimensional modes in sequence at Re=275, when spinning up the cylinder slowly from α=0 to α=4. The hydrogen bubbles wire is placed upstream and parallel to the cylinder; a laser sheet is used for illumination. Initially, mode B can be seen in the non-rotating cylinder wake, and for very low rotation rates. The subharmonic mode C becomes very clear at α>1.2. Modes D and E follow in quick succession at around 1.8<α<2. Mode E appears suddenly at α≈2.1 on the surface of the cylinder, and persists until α=4. The laser is moved slowly in cross-stream direction to show the structure of the wake more clearly.

Download Radi et al. supplememntary movie(Video)
Video 16.4 MB

Radi et al. supplementary movie

The rotating cylinder wake is shown at Re=200, α=4.5. For these conditions, two-dimensional one-sided shedding (`second shedding' or `mode II') have been described by other researchers. The present video shows a highly three-dimensional wake and the absence of two-dimensional periodic shedding.

Download Radi et al. supplementary movie(Video)
Video 3.1 MB

Radi et al. supplementary movie

The rotating cylinder wake at Re=100, α=5.1 shows the detachment of several single-sided vortex bends, which resemble the `second shedding' mode described by other researchers. This video suggests that this process is highly three-dimensional. (The hydrogen bubbles wire is placed downstream and parallel to the cylinder.)

Download Radi et al. supplementary movie(Video)
Video 11.2 MB