Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-21T07:55:23.828Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental and numerical studies of convection in a rapidly rotating spherical shell

Published online by Cambridge University Press:  21 May 2007

N. GILLET ,
D. BRITO ,
D. JAULT  and
H. C. NATAF
N. GILLET
Affiliation:
Laboratoire de Géophysique Interne et Tectonophysique, CNRS, Observatoire de Grenoble, Université Joseph–Fourier, Maison des Géosciences, BP 53, 38041 Grenoble Cedex 09, France
D. BRITO
Affiliation:
Laboratoire de Géophysique Interne et Tectonophysique, CNRS, Observatoire de Grenoble, Université Joseph–Fourier, Maison des Géosciences, BP 53, 38041 Grenoble Cedex 09, France
D. JAULT
Affiliation:
Laboratoire de Géophysique Interne et Tectonophysique, CNRS, Observatoire de Grenoble, Université Joseph–Fourier, Maison des Géosciences, BP 53, 38041 Grenoble Cedex 09, France
H. C. NATAF
Affiliation:
Laboratoire de Géophysique Interne et Tectonophysique, CNRS, Observatoire de Grenoble, Université Joseph–Fourier, Maison des Géosciences, BP 53, 38041 Grenoble Cedex 09, France
Get access Rights & Permissions [Opens in a new window]

Abstract

Thermal convection in a rapidly rotating spherical shell is investigated experimentally and numerically. The experiments are performed in water (Prandtl number P=7) and in gallium (P=0.025), at Rayleigh numbers R up to 80 times the critical value in water (up to 6 times critical in gallium) and at Ekman numbers E∼10−6. The measurements of fluid velocities by ultrasonic Doppler velocimetry are quantitatively compared with quasi-geostrophic numerical simulations incorporating a varying β-effect and boundary friction (Ekman pumping). In water, unsteady multiple zonal jets, weaker in amplitude than the non-axisymmetric flow, are experimentally observed and numerically reproduced at moderate forcings (R/Rc<40). In this regime, zonal flows and vortices share the same length scale. Gallium experiments and strongly supercritical convection experiments in water correspond to another regime. In these turbulent flows, the zonal motion amplitude U dominates the non-axisymmetric motion amplitude Ũ. 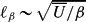As a result of the reverse cascade of kinetic energy, the characteristic Rhines length scale of zonal jets emerges, and the boundary friction becomes the main brake on the growth of the zonal flow. A scaling law U ∼ Ũ4/3 is then derived and verified both numerically and experimentally.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 580 , 10 June 2007 , pp. 83 - 121
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ardes, M., Busse, F. H. & Wicht, J. 1997 Thermal convection in rotating spherical shells. Phys. Earth Planet. Inter. 99, 55–67.CrossRefGoogle Scholar
Aubert, J. 2005 Steady zonal flows in spherical shell fluid dynamos. J. Fluid Mech. 542, 53–67.CrossRefGoogle Scholar
Aubert, J., Brito, D., Nataf, H.-C., Cardin, P. & Masson, J. 2001 A systematic experimental study of rapidly rotating spherical convection in water and liquid gallium. Phys. Earth Planet. Inter. 128, 51–74.CrossRefGoogle Scholar
Aubert, J., Gillet, N. & Cardin, P. 2003 Quasigeostrophic models of convection in rotating spherical shells. Geochem. Geophys. Geosys. 4 (7), 1052.CrossRefGoogle Scholar
Aubert, J., Jung, S. & Swinney, H. 2002 Observations of zonal flows created by potential vorticity mixing in a rotating fluid. Geophys. Res. Lett. 9, 1876–1879.Google Scholar
Aurnou, J. M. & Heimpel, M. 2004 Zonal jets in rotating convection with mixed mechanical boundary conditions. Icarus 169, 492–498.CrossRefGoogle Scholar
Aurnou, J. M. & Olson, P. L. 2001 Strong zonal winds in the major planets. Geophys. Res. Lett. 28, 153–174.Google Scholar
Brito, D. 1998 Approches expérimentales et théoriques de la dynamique du noyau terrestre. PhD thesis, Université Paris VII.Google Scholar
Brito, D., Nataf, H.-C., Cardin, P., Aubert, J. & Masson, J. 2001 Ultrasonic Doppler velocimetry in liquid gallium. Exps. Fluids 31, 653–663.CrossRefGoogle Scholar
Busse, F. 1970 Thermal instabilities in rapidly rotating systems. J. Fluid Mech. 44, 441–460.CrossRefGoogle Scholar
Busse, F. 1986 Asymptotic theory of convection in a rotating, cylindrical annulus. J. Fluid Mech. 173, 545–556.CrossRefGoogle Scholar
Busse, F. & Carrigan, C. 1976 Convection induced by centrifugal buoyancy. J. Fluid Mech. 62, 579–592.CrossRefGoogle Scholar
Busse, F. & Or, A. C. 1986 Convection in a rotating cylindrical annulus. Part 1. Thermal Rossby waves. J. Fluid Mech. 166, 173–187.CrossRefGoogle Scholar
Cardin, P. & Olson, P. 1992 An experimental approach to thermochemical convection in the Earth's core. Geophys. Res. Lett. 19, 1995–1998.CrossRefGoogle Scholar
Cardin, P. & Olson, P. 1994 Chaotic thermal convection in a rapidly rotating spherical shell: consequences for flow in the outer core. Phys. Earth Planet. Inter. 82, 235–239.CrossRefGoogle Scholar
Carrigan, C. R. & Busse, F. H. 1983 An experimental and theoretical investigation of the onset of convection in rotating spherical shells. J. Fluid Mech. 126, 287–305.CrossRefGoogle Scholar
Chamberlain, J. A. & Carrigan, C. R. 1986 An experimental investigation of convection in a rotating sphere subject to time varying thermal boundary conditions. Geophys. Astrophys. Fluid Dyn. 35, 303–327.CrossRefGoogle Scholar
Chen, C. X. & Zhang, K. 2002 Nonlinear convection in a rotating annulus with a finite gap. Geophys. Astrophys. Fluid Dyn. 96, 499–518.CrossRefGoogle Scholar
Christensen, U. R. 2001 Zonal flow driven by deep convection in the major planets. Geophys. Res. Lett. 13, 2553–2556.CrossRefGoogle Scholar
Christensen, U. R. 2002 Zonal flow driven by strongly supercritical convection in rotating spherical shells. J. Fluid Mech. 470, 115–133.CrossRefGoogle Scholar
Christensen, U. R. & Tilgner, A. 2004 Power requirement of the geodynamo from ohmic losses in numerical and laboratory dynamos. Nature 429, 169–171.CrossRefGoogle ScholarPubMed
Cordero, S. & Busse, F. H. 1992 Experiments on convection in rotating hemispherical shells – Transition to a quasi-periodic state. Geophys. Res. Lett. 19, 733–736.CrossRefGoogle Scholar
Danilov, S. & Gurarie, D. 2002 Rhines scale and spectra of the beta-plane turbulence with bottom drag. Phys. Rev. E 65, 067301.Google ScholarPubMed
Danilov, S. & Gurarie, D. 2004 Scaling, spectra and zonal jets in beta-plane turbulence. Phys. Fluids 16, 2592–2602.CrossRefGoogle Scholar
De, Wijs, G., Kresse, G., Vocadlo, L., Dobson, D., Alfè, D., Gillan, M. J. & Price, G. D. 1998 The viscosity of liquid iron at the physical conditions of the Earth's core. Nature 392, 805–807.Google Scholar
Dormy, E., Soward, A. M., Jones, C. A., Jault, D. & Cardin, P. 2004 The onset of thermal convection in rotating spherical shells. J. Fluid Mech. 501, 43–70.CrossRefGoogle Scholar
Dormy, E., Valet, J.-P. & Courtillot, V. 2000 Numerical models of the geodynamo and observational constraints. Geochem. Geophys. Geosys. 1, 62.CrossRefGoogle Scholar
Dumberry, M. & Bloxham, J. 2003 Torque balance, Taylor's constraint and torsional oscillations in a numerical model of the geodynamo. Phys. Earth Planet. Inter. 140, 29–51.CrossRefGoogle Scholar
Gailitis, A., Lielausis, O., Dement'ev, S., Platacis, E., Cifersons, A., Gerbeth, G., Gundrum, T., Stefani, F., Christen, M., Hänel, H. & Will, G. 2000 Detection of a flow induced magnetic field eigenmode in the Riga dynamo facility. Phys. Rev. Lett. 84, 4365–4368.CrossRefGoogle ScholarPubMed
Galperin, B., Nakano, H., Huang, H.-P. & Sukoriansky, S. 2004 The ubiquitous zonal jets in the atmospheres of giant planets and Earth's ocean. Geophys. Res. Lett. 31, L13303.CrossRefGoogle Scholar
Gillet, N. 2004 Magnéto-convection dans une sphère en rotation rapide: approches experimentale et numérique de la convection dans les noyaux planetaires. PhD thesis, Université Joseph-Fourier (Grenoble I).Google Scholar
Gillet, N., Brito, D., Jault, D. & Nataf, H.-C. 2007 Experimental and numerical studies of magnetoconvection in a rapidly rotating spherical shell. J. Fluid Mech. 580, 123–143.CrossRefGoogle Scholar
Gillet, N. & Jones, C. A. 2006 The quasi-geostrophic model for rapidly rotating spherical convection outside the tangent cylinder. J. Fluid Mech. 554, 343–369.CrossRefGoogle Scholar
Gilman, P. A. 1977 Nonlinear dynamics of Boussinesq convection in a deep rotating spherical shell–I. Geophys. Astrophys. Fluid Dyn. 8, 93–135.CrossRefGoogle Scholar
Gilman, P. A. 1978 a Nonlinear dynamics of Boussinesq convection in a deep rotating spherical shell–II: effect of temperature boundary conditions. Geophys. Astrophys. Fluid Dyn. 11, 157–179.CrossRefGoogle Scholar
Gilman, P. A. 1978 b Nonlinear dynamics of Boussinesq convection in a deep rotating spherical shell–III: effect of velocity boundary conditions. Geophys. Astrophys. Fluid Dyn. 11, 181–203.CrossRefGoogle Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Heimpel, M., Aurnou, J. & Wicht, J. 2005 Simulation of equatorial and high-latitude jets on Jupiter in a deep convection model. Nature 438, 193–196.CrossRefGoogle Scholar
Herrmann, J. & Busse, F. H. 1997 Convection in a rotating cylindrical annulus. Part 4. Modulations and transition to chaos at low Prandtl numbers. J. Fluid Mech. 350, 209–229.CrossRefGoogle Scholar
Hide, R. & James, I. N. 1983 Differential rotation produced by potential vorticity mixing in a rapidly rotating fluid. Geophys. J. R. Astron. Soc. 74, 301–312.CrossRefGoogle Scholar
Hide, R., Lewis, S. R. & Read, P. L. 1994 Sloping convection: a paradigm for large-scale waves and eddies in planetary atmospheres? Chaos 4, 135–162.CrossRefGoogle ScholarPubMed
Hide, R. & Mason, P. J. 1970 Baroclinic waves in a rotating fluid subject to internal heating. Phil. Trans. R. Soc. Lond. A 268, 201–232.Google Scholar
Hulot, G., Eymin, C., Langlais, B., Mandea, M. & Olsen, N. 2002 Small scale structure of the geodynamo inferred from Oersted and Magsat satellite data. Nature 416, 620–623.CrossRefGoogle ScholarPubMed
Ingersoll, A., Beebe, R. F., Mitchell, J. L., Garneau, G. W., Yagi, G. M. & Müller, J.-P. 1981 Interaction of eddies and mean zonal flow on Jupiter as inferred from Voyager 1 and 2 images. J. Geophys. Res. 86, 8733–8743.CrossRefGoogle Scholar
Ingersoll, A. & Pollard, D. 1982 Motions in the interiors and atmospheres of Jupiter and Saturn: scale analysis, anelastic equations, barotropic stability criterion. Icarus 52, 62–80.CrossRefGoogle Scholar
Jackson, A. 2003 Intense equatorial flux spots on the surface of the Earth's core. Nature 424, 760–763.CrossRefGoogle ScholarPubMed
Jones, C. A. 2003 Dynamos in planets. In Stellar Astrophysical Fluid Dynamics (ed. Thompson, M. J. & Christensen-Dalsgaard, J.). Cambridge University Press.Google Scholar
Jones, C. A., Rotvig, J. & Abdulrahman, A. 2003 Multiple jets and zonal flows on jupiter. Geophys. Res. Lett. 30, 1731.CrossRefGoogle Scholar
Jones, C. A., Soward, A. N. & Mussa, A. I. 2000 The onset of convection in a rapidly rotating sphere. J. Fluid Mech. 405, 157–179.CrossRefGoogle Scholar
Kono, M. & Roberts, P. H. 2002 Recent geodynamo simulations and observations of the geomagnetic field. Rev. Geophys. 40, 1013.CrossRefGoogle Scholar
Manin, D. 1990 Characteristic size of vortices in developped quasi-two-dimensional flows. Izv. Akad. Nauk. SSSR, Atmos. Ocean. Phys. 26 (6), 426–429.Google Scholar
Manneville, J. & Olson, P. 1996 Banded convection in rotating fluid spheres and the circulation of the Jovian atmosphere. Icarus 122, 242–250.CrossRefGoogle Scholar
Morin, V. & Dormy, E. 2004 Time dependent beta-convection in rapidly rotating spherical shell. Phys. Fluids 16, 1603–1609.CrossRefGoogle Scholar
Or, A. C. & Busse, F. 1987 Convection in a rotating cylindrical annulus. Part 2. Transitions to asymmetric and vacillating flow. J. Fluid Mech. 174, 313–326.CrossRefGoogle Scholar
Plaut, E. & Busse, F. 2002 Low prandtl number convection in a rotating cylindrical annulus. J. Fluid Mech. 464, 345–363.CrossRefGoogle Scholar
Plaut, E. & Busse, F. 2005 Multicellular convection in rotating annuli. J. Fluid Mech. 528, 119–133.CrossRefGoogle Scholar
Read, P. L. 1986 Regimes of axisymmetric flow in an internally heated rotating fluid. J. Fluid Mech. 168, 225–289.CrossRefGoogle Scholar
Read, P. L., Lewis, S. R. & Hide, R. 1997 Laboratory and numerical studies of baroclinic waves in an internally heated rotating fluid annulus: a case of wave/vortex duality? J. Fluid Mech. 337, 155–191.CrossRefGoogle Scholar
Read, P. L., Yamazaki, Y. H., Lewis, S. R., Williams, P. D., Miki-Yamazaki, K., Sommeria, J., Didelle, H. & Fincham, A. 2004 Jupiter's and Saturn's convectively driven banded jets in the laboratory. Geophys. Res. Lett. 31, L22701.CrossRefGoogle Scholar
Rhines, P. B. 1975 Wave and turbulence on a beta-plane. J. Fluid Mech. 122, 417–443.CrossRefGoogle Scholar
Rhines, P. B. & Young, W. 1982 Homogeneization of potential vorticity in planetary gyres. J. Fluid Mech. 122, 347–367.CrossRefGoogle Scholar
Roberts, P. H. 1968 On the thermal instability of a self-graviting fluid sphere containing heat sources. Phil. Trans. R. Soc. Lond. A 263, 93–117.Google Scholar
Schaeffer, N. & Cardin, P. 2005 Quasi-geostrophic model of the instabilities of the stewartson layer in flat and depth varying containers. Phys. Fluids 17, 104111.CrossRefGoogle Scholar
Schnaubelt, M. & Busse, F. H. 1992 Convection in a rotating cylindrical annulus. Part 3. Vacillating and spatially modulated flows. J. Fluid Mech. 245, 155–173.CrossRefGoogle Scholar
Secco, R. A. & Schloessin, H. H. 1989 The electrical resistivity of solid and liquid Fe at pressures up to 7 GPa. J. Geophys. Res. 94, 5887–5894.CrossRefGoogle Scholar
Shew, W. & Lathrop, D. P. 2005 Liquid sodium model of geophysical core convection. Phys. Earth Planet. Inter. 153, 136–149.CrossRefGoogle Scholar
Starchenko, S. & Jones, C. 2002 Typical velocities and magnetic field strengths in planetary interiors. Icarus 157, 426–435.CrossRefGoogle Scholar
Stewartson, K. 1966 On almost rigid rotation. Part 2. J. Fluid Mech. 26, 131–144.CrossRefGoogle Scholar
Stieglitz, R. & Müller, U. 2001 Experimental demonstration of a homogeneous two-scale dynamo. Phys. Fluids 13, 561–564.CrossRefGoogle Scholar
Sumita, I. & Olson, P. 2000 Laboratory experiments on high rayleigh number thermal convection in a rapidly rotating hemispherical shell. Phys. Earth Planet. Inter. 117, 153–170.CrossRefGoogle Scholar
Sumita, I. & Olson, P. 2003 Experiments on highly supercritical thermal convection in a rapidly rotating hemispherical shell. J. Fluid Mech. 492, 271–287.CrossRefGoogle Scholar
Takahashi, F., Matsushima, M. & Honkura, Y. 2005 Simulations of a quasi-Taylor state geomagnetic field including polarity reversals on the earth simulator. Science 309, 459–461.CrossRefGoogle ScholarPubMed
Tilgner, A. & Busse, F. H. 1997 Finite amplitude convection in rotating spherical fluid shells. J. Fluid Mech. 332, 359–376.CrossRefGoogle Scholar
Van, de Konijnenberg, J. A., Nielsen, A. H., Rasmussen, J. J. & Stenum, B. 1998 Shear-flow instability in a rotating fluid. J. Fluid Mech. 387, 177–204.Google Scholar
Williams, G. 1978 Planetary circulations: 1. Barotropic representation of jovian and terrstrial turbulence. J. Atmos. Sci. 35, 1399–1426.2.0.CO;2>CrossRefGoogle Scholar
Yano, J., Talagrand, O. & Drossart, P. 2003 Outer planets: Origins of atmospheric zonal winds. Nature 421, 36.CrossRefGoogle ScholarPubMed
Yano, J.-I. 1992 Asymptotic theory of thermal convection in rapidly rotating systems. J. Fluid Mech. 236, 535–556.Google Scholar
Zhang, K. 1992 a On inertial waves in the earth's fluid core. Geophys. Res. Lett. 19, 737–740.CrossRefGoogle Scholar
Zhang, K. 1992 b Spiralling columnar convection in rapidly rotating spherical fluid shell. J. Fluid Mech. 236, 535–556.CrossRefGoogle Scholar
Zhang, K. 1993 On equatorially trapped boundary inertial waves. J. Fluid Mech. 248, 203–217.CrossRefGoogle Scholar
Zhang, K. & Busse, F. H. 1987 On the onset of convection in rotating spherical shells. Geophys. Astrophys. Fluid Dyn. 39, 119–147.CrossRefGoogle Scholar
Zhang, K. & Jones, C. A. 1992 The influence of Ekman boundary layers on rotating convection. Geophys. Astrophys. Fluid Dyn. 71, 145–162.CrossRefGoogle Scholar