Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-10T04:06:48.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact two-dimensionalization of low-magnetic-Reynolds-number flows subject to a strong magnetic field

Published online by Cambridge University Press:  20 May 2015

Basile Gallet  and
Charles R. Doering
Basile Gallet*
Affiliation:
Service de Physique de l’État Condensé, DSM, CNRS UMR 3680, CEA Saclay, 91191 Gif-sur-Yvette, France
Charles R. Doering
Affiliation:
Department of Physics, Department of Mathematics and Center for the Study of Complex Systems, University of Michigan, Ann Arbor, MI 48109, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the behaviour of flows, including turbulent flows, driven by a horizontal body force and subject to a vertical magnetic field, with the following question in mind: for a very strong applied magnetic field, is the flow mostly two-dimensional, with remaining weak three-dimensional fluctuations, or does it become exactly 2-D, with no dependence along the vertical direction? We first focus on the quasi-static approximation, i.e. the asymptotic limit of vanishing magnetic Reynolds number, $\mathit{Rm}\ll 1$: we prove that the flow becomes exactly 2-D asymptotically in time, regardless of the initial condition and provided that the interaction parameter 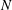$N$ is larger than a threshold value. We call this property absolute two-dimensionalization: the attractor of the system is necessarily a (possibly turbulent) 2-D flow. We then consider the full magnetohydrodynamic (MHD) equations and prove that, for low enough 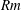$\mathit{Rm}$ and large enough 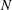$N$, the flow becomes exactly 2-D in the long-time limit provided the initial vertically dependent perturbations are infinitesimal. We call this phenomenon linear two-dimensionalization: the (possibly turbulent) 2-D flow is an attractor of the dynamics, but it is not necessarily the only attractor of the system. Some 3-D attractors may also exist and be attained for strong enough initial 3-D perturbations. These results shed some light on the existence of a dissipation anomaly for MHD flows subject to a strong external magnetic field.

JFM classification

MHD and Electrohydrodynamics: High-Hartmann-number flows MHD and Electrohydrodynamics: MHD and Electrohydrodynamics MHD and Electrohydrodynamics: MHD turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 773 , 25 June 2015 , pp. 154 - 177
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alemany, A., Moreau, R., Sulem, P. L. & Frisch, U. 1979 Influence of an external magnetic field on homogeneous MHD turbulence. J. Méc. 18 (2), 277–313.Google Scholar
Alexakis, A. 2011 Two-dimensional behavior of three-dimensional magnetohydrodynamic flow with a strong guiding field. Phys. Rev. E 84, 056330.CrossRefGoogle Scholar
Alexakis, A. & Doering, C. R. 2006 Energy and enstrophy dissipation in steady state 2d turbulence. Phys. Lett. A 359, 652–657.CrossRefGoogle Scholar
Bigot, B. & Galtier, S. 2011 Two-dimensional state in driven magnetohydrodynamic turbulence. Phys. Rev. E 83 (2), 026405.CrossRefGoogle Scholar
Davidson, P. A. 1999 Magnetohydrodynamic in materials processing. Annu. Rev. Fluid Mech. 31, 273–300.CrossRefGoogle Scholar
Doering, C. R. & Foias, C. 2002 Energy dissipation in body-forced turbulence. J. Fluid Mech. 467, 289–306.CrossRefGoogle Scholar
Gallet, B., Berhanu, M. & Mordant, N. 2009 Influence of an external magnetic field on forced turbulence in a swirling flow of liquid metal. Phys. Fluids 21, 085107.CrossRefGoogle Scholar
Gallet, B., Herault, J., Laroche, C., Pétrélis, F. & Fauve, S. 2012 Reversals of a large-scale field generated over a turbulent background. Geophys. Astrophys. Fluid Dyn. 106, 468–492.CrossRefGoogle Scholar
Gallet, B., Pétrélis, F. & Fauve, S. 2012 Dynamo action due to spatially dependent magnetic permeability. Europhys. Lett. 97, 69001.CrossRefGoogle Scholar
Gallet, B., Pétrélis, F. & Fauve, S. 2013 Spatial variations of magnetic permeability as a source of dynamo action. J. Fluid Mech. 727, 161–190.CrossRefGoogle Scholar
Gissinger, C., Iskakov, A., Fauve, S. & Dormy, E. 2008 Effect of magnetic boundary conditions on the dynamo threshold of von Kármán swirling flows. Europhys. Lett. 82, 29001.CrossRefGoogle Scholar
Herault, J. & Pétrélis, F. 2014 Optimum reduction of the dynamo threshold by a ferromagnetic layer located in the flow. Phys. Rev. E 90, 033015.CrossRefGoogle ScholarPubMed
Klein, R. & Pothérat, A. 2010 Appearance of three-dimensionality in wall-bounded MHD flows. Phys. Rev. Lett. 104 (3), 034502.CrossRefGoogle ScholarPubMed
Knaepen, B. & Moreau, R. 2008 Magnetohydrodynamic turbulence at low magnetic Reynolds number. Annu. Rev. Fluid Mech. 40, 25–45.CrossRefGoogle Scholar
Ladyzhenskaya, O. A. 1963 The Mathematical Theory of Viscous Incompressible Flow. Gordon and Breach.Google Scholar
Lingwood, R. J. & Alboussière, T. 1999 On the stability of the Hartmann layer. Phys. Fluids 11, 2058–2068.CrossRefGoogle Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Moresco, P. & Alboussière, T. 2004 Experimental study of the instability of the Hartmann layer. J. Fluid Mech. 504, 167–181.CrossRefGoogle Scholar
Pothérat, A. & Alboussière, T. 2003 Small scales and anisotropy in low Rm magnetohydrodynamic turbulence. Phys. Fluids 15, 3170–3180.CrossRefGoogle Scholar
Pothérat, A. & Klein, R. 2014 Why, how and when MHD turbulence at low $Rm$ becomes three-dimensional. J. Fluid Mech. 761, 168–205.CrossRefGoogle Scholar
Sommeria, J. 1986 Experimental study of the two-dimensional inverse energy cascade in a square box. J. Fluid Mech. 170, 139–168.CrossRefGoogle Scholar
Sommeria, J. & Moreau, R. 1982 Why, how, and when, MHD turbulence becomes two-dimensional. J. Fluid Mech. 118, 507–518.CrossRefGoogle Scholar
Thess, A. & Zikanov, O. 2007 Transition from two-dimensional to three-dimensional magnoethydrodynamic turbulence. J. Fluid Mech. 579, 338–412.CrossRefGoogle Scholar
Zikanov, O. & Thess, A. 1998 Direct numerical simulation of forced MHD turbulence at low magnetic Reynolds number. J. Fluid Mech. 358, 299–333.CrossRefGoogle Scholar